ОГЭ
Задание 2670
ABC – равнобедренный треугольник с основанием AC, CD – биссектриса угла C, ∠ADC = 150°. Найдите ∠B.
|
1) Пусть $$\angle A=\angle C=x$$ $$\Rightarrow$$ $$\angle ACD=\frac{x}{2}$$ (CD-биссектриса) 2) $$x+\frac{x}{2}+150=180^{\circ}$$ (из $$\bigtriangleup ADC$$) $$1,5x=30$$ $$\Rightarrow$$ $$x=20^{\circ}$$ 3) $$\angle B=180^{\circ}-2x=180^{\circ}-40^{\circ}=140^{\circ}$$ |
 |
Задание 2774
Точка М лежит внутри равнобедренного треугольника АВС с основанием АС на расстоянии 6 см от боковых сторон и на расстоянии $$\sqrt{3}$$ см от основания. Найдите основание треугольника, если $$\angle B=120^{\circ}$$.
|
1) $$\bigtriangleup BMC$$ - прямоугольный: $$\frac{CM}{BM}=\sin 60^{\circ}=\frac{\sqrt{3}}{2}$$; $$\frac{6}{BM}=\frac{\sqrt{3}}{2}$$ $$\Rightarrow$$ $$BM=\frac{12}{\sqrt{3}}=4\sqrt{3}$$ 2) $$BK=BM+MK=4\sqrt{3}+\sqrt{3}=5\sqrt{3}$$ 3) $$\tan 60^{\circ}=\frac{AK}{BK}$$ (из $$\bigtriangleup ABK$$) $$\sqrt{3}=\frac{x}{5\sqrt{3}}$$ $$\Rightarrow$$ $$x=15$$ $$\Rightarrow$$ $$AC=15\cdot2=30$$ |
Задание 2816
Сторона АВ треугольника АВС разделена на три равные части и через точки деления проведены прямые, параллельные стороне АС. Найдите площадь трапеции, заключенной между ними, если площадь треугольника равна 93.
|
$$\bigtriangleup BKP\sim \bigtriangleup BML\sim \bigtriangleup ABC$$ $$BK=\frac{1}{3}AB$$ $$\Rightarrow$$ $$S_{KBP}=\frac{1}{9}S_{ABC}=\frac{1}{9}\cdot93=10\frac{1}{3}$$ |
Задание 2928
Окружность с центром О вписана в прямоугольный треугольник АВС. Она касается гипотенузы АВ в точке М, причем АМ = 12 и ВМ = 8. Найдите площадь треугольника АОВ.
Решение временно отсутствует, можете найти его в моем видео-разборе ( вначале варианта )
Задание 2977
В треугольнике ABC высота BD = 11,2 см, а высота AE = 12см. Точка E делит сторону BC в отношении 5:9, считая от вершины B. Найти длину стороны AC.
Текстовое решение временно отсутствует. Вы можете найти разбор в видео перед вариантом
Задание 3018
Найдите площадь прямоугольного треугольника, если длина гипотенузы равна $$2\sqrt{13}$$ см, а длина медианы, проведенной из вершины большего острого угла равна 5 см.
|
Пусть $$AC=x$$; $$CB=2y$$ Из $$\bigtriangleup ACH$$ и $$\bigtriangleup ACB$$: $$\left\{\begin{matrix}x^{2}+y^{2}=5^{2}\\x^{2}-(2y)^{2}=(2\sqrt{13})^{2}\end{matrix}\right.$$ $$4y^{2}-y^{2}=4\cdot13-25$$ $$3y^{2}=27\Rightarrow y^{2}=9\Rightarrow y=3$$ $$x^{2}+9=25\Rightarrow x=4$$ $$S=\frac{1}{2}AC\cdot CB=\frac{1}{2}\cdot x\cdot 2y=xy=3\cdot 4=12$$ |
Задание 3142
Найдите катеты прямоугольного треугольника, если его гипотенуза равна 20, а радиус вписанной окружности равен 4.
Текстовое решение временно недоступно, вы можете найти его в видео в начале варианта
Задание 3567
В треугольнике АВС АВ = ВС = 4см. АЕ = 3 см – медиана треугольника. Найдите АС.
1) из $$\bigtriangleup ABE$$:
$$\cos B=\frac{AB^{2}+BE^{2}-AE^{2}}{2AB\cdot BC}=\frac{4^{2}+2^{2}-3^{2}}{2\cdot4\cdot2}=\frac{16+4-9}{16}=\frac{11}{16}$$
2) из $$\bigtriangleup ABC$$:
$$AC=\sqrt{AB^{2}+BC^{2}-2AB\cdot BC\cdot\cos B}=\sqrt{4^{2}+4^{2}-2\cdot4\cdot4\cdot\frac{11}{16}}=\sqrt{32-22}=\sqrt{10}$$
Задание 4329
В треугольнике АВС АС=АВ, медианы АМ и ВF пересекаются в точке О, АМ:ВF=8:5.Найдите BF, если площадь треугольника AOF равна 24.
1) Пусть $$S_{ABC}=S$$, тогда $$S=2\cdot\frac{1}{2}\cdot AC\cdot AM\sin\alpha=AC\cdot AM\sin\alpha$$; $$S_{AFO}=\frac{1}{2}\cdot AF\cdot AO\sin\alpha=$$ $$\frac{1}{2}\cdot\frac{1}{2}AC\cdot\frac{2}{3}AM\sin\alpha=\frac{1}{6}AC\cdot AM\sin\alpha=24$$ $$\Rightarrow$$ $$AC\cdot AM\sin\alpha=144=S$$ $$\Rightarrow$$ $$\frac{1}{2}AM\cdot CB=144$$
2) Пусть $$AM=8x$$ $$\Rightarrow$$ $$BF=5x$$, по свойству медиан: $$OB=\frac{2}{3}BF=\frac{10x}{3}$$; $$OM=\frac{1}{3}AM=\frac{8x}{3}$$; $$MB=\sqrt{OB^{2}-OM^{2}}=\sqrt{(\frac{10x}{3})^{2}-(\frac{8x}{3})^{2}}=\frac{6x}{3}=2x$$ $$\Rightarrow$$ $$CB=4x$$
3) $$\frac{1}{2}AM\cdot CB=144$$; $$\frac{1}{2}\cdot8x\cdot4x=144$$; $$32x^{2}=288$$; $$x^{2}=9$$ $$x=3$$
4) $$BF=5x=5\cdot3=15$$
Задание 4535
Основание равнобедренного треугольника равно 12 см, а высота, проведенная к боковой стороне, равна 9,6 см. Найдите периметр треугольника
1) Проведем $$BM\perp AC$$ $$\Rightarrow$$ $$\bigtriangleup BMC\sim\bigtriangleup AHC$$ (прямоугольные; $$\angle C$$ - общий)
2) $$MC=\frac{1}{2}AC=6$$; $$HC=\sqrt{12^{2}-9,6^{2}}=7,2$$;
3) $$\frac{BM}{AH}=\frac{MC}{HC}$$ $$\Rightarrow$$ $$BM=\frac{AH\cdot MC}{HC}=\frac{9,6\cdot6}{7,2}=8$$
4)$$BC=\sqrt{MC^{2}+BM^{2}}=10=AB$$
$$P_{ABC}=10+10+12=32$$
Задание 4652
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
Выполним построение:
Задание 4897
Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два треугольника, площади которых равны соответственно 6 и 54. Найдите гипотенузу треугольника
Задание 5224
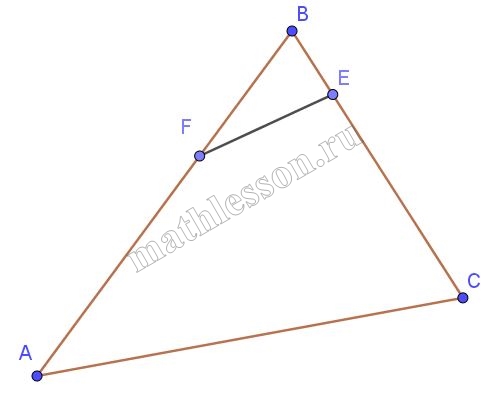
На сторонах ВС и ВА треугольника АВС взяты точки E и F такие, что ВE:EС=1:3, ВF:FА=1:2. Площадь треугольника BEF равна 10. Найти площадь треугольника АВС
$$\frac{S_{ABC}}{S_{BEF}}=\frac{AB*BC}{BF*BE}(1)$$. Так как ВE:EС=1:3, то BC=4BE, так как ВF:FА=1:2, то AB=3BF. Подставим данные выражения в формулу (1): $$\frac{S_{ABC}}{S_{BEF}}=\frac{3BF*4BE}{BF*BE}=12$$, тогда $$S_{ABC}=12S_{BFE}=12*10=120$$