Неравенства

Пусть $$a=2, b=1$$ (подобрали числа, чтобы выполнялось неравенство a>b). Проверим правильность представленных вариантов:

1. $$a-b< -3\Leftrightarrow$$$$2-1< -3\Leftrightarrow$$$$1< -3$$ - неверно
2. $$b-a> 1\Leftrightarrow$$$$1-2> 1\Leftrightarrow$$$$-1>1$$ - неверно
3. $$b-a< 2\Leftrightarrow$$$$1-2< 2\Leftrightarrow$$$$-1< 2$$ - верно
4. Верно 1,2 и 3

Верным оказался только третий вариант

Подберем любые значения a и b, чтобы выполнялось неравенство, предаставленное на рисунке (a>c). Пусть $$a=2, c=1$$. Проверим истинность представленных вариантов:

1. $$a-1>c-1\Leftrightarrow$$$$2-1>1-1\Leftrightarrow$$$$1>0$$ - верно
2. $$-a<-c\Leftrightarrow$$$$-2<-1$$ - верно
3. $$\frac{a}{6}<\frac{c}{6}\Leftrightarrow$$$$\frac{2}{6}<\frac{1}{6}$$ - неверно
4. $$a+3>c+1\Leftrightarrow$$$$2+3>1+1\Leftrightarrow$$$$5>2$$ - верно

Неверным является вариант под номером 3

Выполним преобразования с каждым из представленных вариантов:

1. $$y>z+x|-x\Leftrightarrow$$$$y-x>z$$ - получили первоначальное неравенство
2. $$y-x-z<0|+z\Leftrightarrow$$$$y-x<z$$ - не получили первоначальное неравенство
3. $$z+x-y<0|-z|*(-1)\Leftrightarrow$$$$y-x>z$$ - получили первоначальное неравенство
4. $$y-z>x|-x+z\Leftrightarrow$$$$y-x>z$$ - получили первоначальное неравенство

Не получили только во втором варианте ответа

Пусть $$a=2, b=1$$ (подобрали числа, чтобы выполнялось неравенство a>b>0). Проверим правильность представленных вариантов:

1. $$2a+1<0\Leftrightarrow$$$$2*2+1<0\Leftrightarrow$$$$5<0$$ - неверно
2. $$-a>-b\Leftrightarrow$$$$-2>-1$$ - неверно
3. $$2b>2a\Leftrightarrow$$$$2*1>2*2\Leftrightarrow$$$$2>4$$ - неверно
4. $$1-a<1-b\Leftrightarrow$$$$1-2<1-1\Leftrightarrow$$$$-1<0$$ - верно

Верным оказался только 4 вариант ответа

Выберем значение а в соответствии с представленным рисунком: $$-5<a<-4$$. Пусть $$a=-4,5$$. Проверим верность представлнных утверждений:

1. $$a+4>0\Leftrightarrow$$$$-4,5+4>0\Leftrightarrow$$$$-0,5>0$$ - неверно
2. $$a+5<0\Leftrightarrow$$$$-4,5+5<0\Leftrightarrow$$$$0,5<0$$ - неверно
3. $$2-a>0\Leftrightarrow$$$$2-(-4,5)>0\Leftrightarrow$$$$6,5>0$$ - верно
4. $$3-a<0\Leftrightarrow$$$$3-(-4,5)<0\Leftrightarrow$$$$7,5<0$$ - неверно

Верным оказался только третий вариант ответа

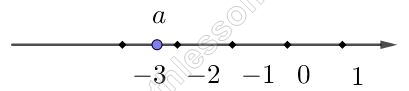
Выберем значение а в соответствии с условием задачи: $$-3<a<-2$$. Пусть $$a=-2,5$$. Проверим истинность представленных варинатов:

1. $$-a<2\Leftrightarrow$$$$-(-2,5)<0\Leftrightarrow$$$$2,5<0$$ - неверно
2. $$-1-a>0\Leftrightarrow$$$$-1-(-2,5)>0\Leftrightarrow$$$$1,5>2$$ - верно
3. $$\frac{1}{a}>0\Leftrightarrow$$$$\frac{1}{-2,5}>0\Leftrightarrow$$$$-0,4>0$$ - неверно
4. $$a+3<0\Leftrightarrow$$$$-2,5+3<0\Leftrightarrow$$$$0,5<0$$ - неверно

Верным оказался только 2 вариант ответа

Подберем числа a, b и c в соответствии с условиями задачи: $$a<b<0<c$$. Пусть $$a=-2 ; b=-1 ; c=1,5$$. Проверим истинность представленнх вариантов ответов:

1. $$a+b>0\Leftrightarrow$$$$-2+(-1)>0\Leftrightarrow$$$$-3>0$$ - неверно
2. $$\frac{1}{b}>\frac{1}{c}\Leftrightarrow$$$$\frac{1}{-1}>\frac{1}{1}\Leftrightarrow$$$$-1>1$$ - неверно
3. $$ab<0\Leftrightarrow$$$$(-2)*(-1)<0\Leftrightarrow$$$$2<0$$ - неверно
4. $$(a-b)c<0\Leftrightarrow$$$$(-2-(-1))*1<0\Leftrightarrow$$$$-1<0$$ - верно

Верным является только вариант под номером 4

Возьмем приблизительное значение числа a  с учетом его расположения a>6. Пусть $$a=6,5$$, тогда:

1. $$a-6>0\Leftrightarrow$$$$6,5-6>0\Leftrightarrow$$$$0,5>0$$ - верно
2. $$5-a<0\Leftrightarrow$$$$5-6,5<0\Leftrightarrow$$$$-1,5<0$$ - верно
3. $$a-1>0\Leftrightarrow$$$$6,5-1>0\Leftrightarrow$$$$5,5>0$$ - верно
4. $$0-a>0\Leftrightarrow$$$$0-6,5>0\Leftrightarrow$$$$-6,5>0$$ - неверно

Как видим, ответ под номером 4 оказался неверным

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

1) ab => произведение двух отрицательных - число положительное - не подходит 2) (a+b)b => сумма двух отрицательных - число отрицательное, а их произведение - положительное - не подходит 3) (a+b)a => сумма двух отрицательных - число отрицательное, а их произведение - положительное - не подходит 4) -ab => произведение двух отрицательных - число положительное , плюс перед произведением минус, а положительное на отрицательное - число отрицательное - подходит

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть $$a=1>0$$; $$b=-1<0$$

1) $$ab=1\cdot(-1)<0$$

2) $$(a-b)b=(1-(-1))(-1)=-2<0$$

3) $$(b-a)b=(-1-1)\cdot(-1)=2>0$$

4) $$(b-a)\cdot a=(-1-1)\cdot1<0$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть a=-1, b=-2

1. $$ab =(-1)(-2)=2>0$$
2. $$(a+b)b=(-1-2)(-2)=6>0$$
3. $$(a+b)a=(-1-2)(-1)=3>0$$
4. $$-ab=-2<0$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть $$a=-2; b=-1; c=1.$$

$$a+b>0\Leftrightarrow -2-1>0$$ - неверно

$$\frac{1}{b}>\frac{1}{c}\Leftrightarrow \frac{1}{-1}>\frac{1}{1}$$ - неверно

$$ab<0\Leftrightarrow (-2)\cdot(-1)<0$$ - неверно

$$(a-b)\cdot c<0\Leftrightarrow (-2-(-1))\cdot1<0$$ - верно

Заметим, что $$-1<a<0, 0<b<1,$$ откуда $$a^3<0, a-b<0, ab<0, -1<a+b<1.$$ Таким образом, верным является утверждение $$ab<1.$$

Учтём, что $$2,6=\sqrt{2,6^2}=\sqrt{5,76}$$; $$2,8=\sqrt{2,8^2}=\sqrt{7,24}\Rightarrow a=\sqrt{7}\Rightarrow 2$$