ОГЭ
Задание 3144
Точки D и Е расположены на стороне АС треугольника АВС. Прямые ВD и ВЕ разбивают медиану АМ треугольника АВС на три равных отрезка. Найдите площадь треугольника BDE, если площадь треугольника ABC равна 1.
Текстовое решение временно недоступно, вы можете найти его в видео в начале варианта
Задание 2973
Прямая пересекает стороны АВ и АС треугольника АВС в точках Р и М соответственно. Найдите отношение площади треугольника АМР к площади четырехугольника МСВР, если АР : РВ = 5 : 4, АМ : МС = 3 : 5.
1) $$S_{ABC}=\frac{1}{2}AB\cdot AC\cdot \sin A=\frac{1}{2}9x\cdot 8y\cdot \sin \alpha =36xy\sin \alpha$$ 2) $$S_{APM}=\frac{1}{2}AP\cdot AM\cdot \sin A=\frac{1}{2}5x\cdot 3y\cdot \sin \alpha =7,5xy\sin \alpha$$ 3) $$S_{PBCM}=S_{ABC}-S_{APM}=36xy\sin \alpha-7,5xy\sin \alpha=28,5xy\sin \alpha$$ 4) $$\frac{S_{AMP}}{S_{MCBP}}=\frac{7,5xy\sin \alpha}{28,5xy\sin \alpha}=\frac{75}{285}=\frac{15}{57}=\frac{5}{19}$$
Задание 3569
В равностороннем треугольнике АВС высота равна $$\sqrt{3}$$. На стороне АВ взята точка М, такая, что АМ:МВ = 1:3. На стороне ВС взята точка N, такая, что ВN:NС = 3:5.Найдите площадь четырехугольника АМNС.
1) из $$\bigtriangleup AHB$$: $$\sin A=\frac{BH}{AB}$$ $$\Rightarrow$$
$$AB=\frac{BH}{\sin A}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=2$$
2) $$MB=\frac{3}{4}AB$$; $$BN=\frac{3}{8}BC$$ $$\Rightarrow$$
$$S_{BMN}=\frac{1}{2}\cdot\frac{3}{4}AB\cdot\frac{3}{8}BC\cdot\sin B=\frac{9}{32}\cdot\frac{1}{2}AB\cdot BC\cdot\sin B=\frac{9}{32}S_{ABC}$$
3) $$S_{ABC}=\frac{1}{2}\cdot AB\cdot BC\cdot\sin B=\frac{1}{2}\cdot2\cdot2\cdot\frac{\sqrt{3}}{2}=\sqrt{3}$$ $$\Rightarrow$$
$$S_{AMNC}=S_{ABC}-S_{BMN}=\frac{23}{32}S_{ABC}=\frac{23}{32}\cdot\sqrt{3}$$
Задание 4331
Через центр О вписанной в треугольник АВС полуокружности проведена прямая, параллельная стороне ВС и пересекающая стороны АВ и АС соответственно в точках М и N. Периметр треугольника АМN равен 3, ВС = 1, а отрезок АО в 3 раза больше радиуса вписанной в треугольник АВС окружности. Найдите площадь треугольника АВС.
$$S_{ABC}=p\cdot r=\frac{AB+BC+AC}{2}\cdot r$$; $$P_{AMN}=AM+MN+AN$$; BO - биссетриса $$\Rightarrow$$ $$MO\parallel BO$$ $$\Rightarrow$$ $$\angle MOB=\angle OBH=\angle OBM$$ $$\Rightarrow$$ $$\bigtriangleup MBO$$ - равнобедренный $$\Rightarrow$$ $$MB=MO$$. Аналогично: $$ON=NC$$ $$\Rightarrow$$ $$MN=MO+ON=MN+NC$$; $$AB=AM+MB$$; $$AC=AN+NC$$; $$P_{AMN}=AM+AN+NO+OM=AM+AN+NC+MB=AB+AC=3$$
Из $$\bigtriangleup AOP$$: $$AP=\sqrt{AO^{2}-OP^{2}}=\sqrt{(3r)^{2}-r^{2}}=\sqrt{8}r$$; $$S_{ABC}=\frac{AB+BC+AC}{2}\cdot r=\frac{3+1}{2}\cdot r=2r$$; $$AP=\frac{AB+AC-BC}{2}=\frac{3-1}{2}=1$$ $$\Rightarrow$$ $$AP=1=\sqrt{8}r$$ $$\Rightarrow$$ $$r=\frac{1}{\sqrt{8}}$$; $$S_{ABC}=2\cdot\frac{1}{\sqrt{8}}=\frac{1}{\sqrt{2}}$$
Задание 4654
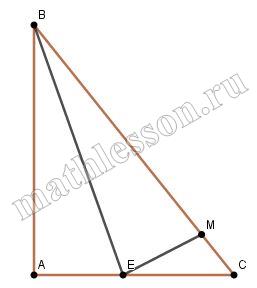
В прямоугольном треугольнике АВС точки D и E лежат соответственно на катетах BC и AC так, что CD = CE = 1. Точка M - точка пересечения отрезков AD и BE Площадь треугольника BMD больше площади треугольника AME на 1/2. Известно, что AD = $$\sqrt{10}$$ . Найдите длину гипотенузы AB.
Построим чертеж:
Задание 4804
В треугольнике, величина одного из углов которого равна разности величин двух других его углов, длина меньшей стороны равна 1, а сумма площадь квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найдите длину большей стороны треугольника.
Построим рисунок:
1) Пусть меньший угол $$\alpha$$, а жва других $$x$$ и $$y$$. По условию задания меньший равен равности двух сотавшихся, а по свойству треугольника разность 180 и меньшего дает сумму оставшихся. Тогда:
$$\left\{\begin{matrix} \alpha= x-y\\180-\alpha =x+y \end{matrix}\right.$$
Сложим оба уравнения системы:
$$\Rightarrow 180=2x \Leftrightarrow x=90$$
То есть мы получили прямоугольный треугольник. Построим новый чертеж по условию задачи и с учетом полученного решения:
2) Пусть $$AC = x ; S_{AEDC}=S_{1}; S_{BCIH}=S_{2}$$. Тогда $$S_{1}=x^{2} ;$$$$ BC=\sqrt{x^{2}-1} \Rightarrow S_{2}=x^{2}-1 \Rightarrow $$$$S_{1}+S_{2}=2x^{2}-1$$
3)Пусть площадь окружности $$S_{3} ; R$$-радиус окружности.Радиус описанной окружотсти вокруг прямоугольного треугольника равен полвине его гипотенузы. $$R=\frac{AC}{2}=\frac{x}{2}$$. Тогда : $$S_{3}=\pi R^{2}=\pi \frac{x^{2}}{4}$$. Приравняем площади: $$2x^{2}-1=2*\pi \frac{x^{2}}{4} \Rightarrow $$$$4x^{2}-2=\pi x^{2} \Rightarrow $$$$x^{2}(4-\pi)=2 \Rightarrow $$$$x=\sqrt{\frac{2}{4-\pi}}$$
Задание 4872
В равностороннем треугольнике АВС из вершин А и В проведена окружность с центром в точке О, проходящая через точку пересечения медиан треугольника АВС и касающаяся его стороны ВС в её середине D. Из точки А проведена прямая, касающаяся этой окружности в точке Е так, что градусная мера угла ВАЕ меньше $$30^{\circ}$$. Найдите отношение площадей треугольника АВЕ и четырехугольника ВЕОD
Задание 4946
На продолжении стороны ВС треугольника АВС за точку В расположена точка Е так, что биссектрисы углов АЕС и АВС пересекаются в точке К, лежащей на стороне АС. Длина отрезка ВЕ = 1, длина отрезка ВС равна 2, градусная мера угла ЕКВ равна $$30^{\circ}$$. Найдите длину стороны АВ.
Задание 5089
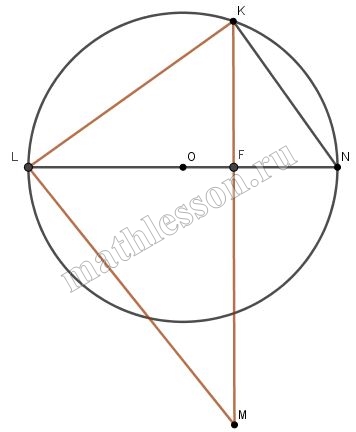
Дан треугольник KLM. Через точки K и L проведена окружность, центр которой лежит на высоте LF, опущенной на сторону KM. Известно, что точка F лежит на стороне KM. Найдите площадь круга, ограниченного этой окружностью, если $$KL=1$$, $$KM=\frac{\sqrt{3}}{2}$$, $$FM=\frac{\sqrt{3}}{6}$$
1) $$KF=KM-FM=\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{6}=\frac{\sqrt{3}}{3}$$
2) $$\bigtriangleup LKF$$: $$LF=\sqrt{KL^{2}-LF^{2}}=\sqrt{1^{2}-\frac{3}{9}}=\frac{\sqrt{6}}{3}$$;
3) $$\bigtriangleup LKN$$ - прямоугольный, т.к. опирается на диаметр $$\Rightarrow$$ $$\bigtriangleup KLF\sim\bigtriangleup LKN$$ (по 2 углам) $$\Rightarrow$$ $$\frac{KL}{LN}=\frac{LF}{KL}$$ $$\Rightarrow$$ $$KL^{2}=LN\cdot LF$$ $$\Rightarrow$$ $$KL^{2}=LF(LF+FN)$$, пусть $$FN=x$$
$$1^{2}=\frac{\sqrt{6}}{3}(\frac{\sqrt{6}}{3}+x)$$; $$1-\frac{6}{9}=\frac{\sqrt{6}}{3}x$$; $$\Rightarrow$$ $$x=\frac{1}{3}\cdot\frac{3}{\sqrt{6}}=\frac{1}{\sqrt{6}}$$; $$LN=LF+FN=\frac{\sqrt{6}}{3}+\frac{1}{\sqrt{6}}=\frac{2\sqrt{6}}{6}+\frac{\sqrt{6}}{6}=$$ $$\frac{3\sqrt{6}}{6}=\frac{\sqrt{6}}{2}$$
4) $$R=\frac{1}{2}LN$$ (радиус описанной вокруг прямоугольного треугольника окружности равен половине гипотенузы) $$\Rightarrow$$ $$R=\frac{\sqrt{6}}{4}$$
5) $$S=\pi R^{2}=\frac{6}{16}\pi=\frac{3}{8}\pi$$
Задание 5176
В прямоугольном треугольнике ABC проведена биссектриса ВЕ, а на гипотенузе ВС взята точка М так, что $$EM \perp BE$$. Найдите площадь треугольника АВС, если СМ=1, СЕ=2..
Задание 5226
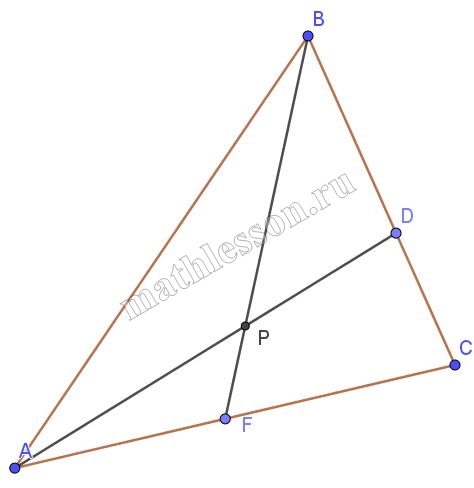
В треугольнике АВС точка D на стороне ВС и точка F на стороне АС расположены так, что ВD:DC=3:2, AF:FC=3:4. Отрезки AD и BF пересекаются в точке Р. Найдите отношение АР:PD.
ВD:DC=3:2, пусть BD=3x, тогда DC=2x, а BC=5x. AF:FC=3:4, пусть AF=3y, тогда FC=4y. По теореме Менелая для треугольника BFC: $$\frac{AP}{PD}*\frac{BD}{BC}*\frac{CF}{AF}=1\Leftrightarrow$$$$\frac{AP}{PD}*\frac{3x}{5x}*\frac{4y}{3y}=1\Leftrightarrow$$$$\frac{AP}{PD}=\frac{5}{4}$$
Задание 5274
Сторона равностороннего треугольника АВС равна 14. Через его центр проведена прямая $$l$$, пересекающая сторону ВС и проходящая на расстоянии $$\sqrt{7}$$ от середины стороны АВ. В каком отношении прямая $$l$$ делит сторону ВС?
Задание 5417
В треугольнике АВС, площадь которого равна S, точка М середина стороны ВС, точка N на продолжении стороны АВ и точка К на продолжении стороны АС выбраны так, что AN = ½ AB, CK = ½ AC. Найти площадь треугольника MNK.
1)$$S_{MCR}=\frac{1}{4}*S$$
2)Пусть $$MR\left | \right |AC\Rightarrow AR=RB$$(RM-средняя линия)$$\Rightarrow AR=0,5*y=NA\Rightarrow AL$$-средняя линия $$\Rightarrow NL=LM\Rightarrow AL=\frac{1}{2}*RM=\frac{1}{4}*AC=\frac{1}{4}x ; LC=\frac{3}{4}x ;$$
3)$$S_{NMK}=S_{MCK}+S_{MCL}+S_{NLK}$$ $$S_{MCL}=\frac{1}{2}*\frac{3}{4}*S=\frac{3}{8}*S\Rightarrow S_{LMK}=\frac{3}{8}*S=\frac{5*S}{8};$$
4)KL-медиана$$\Rightarrow S_{MLK}=S_{KLN}=\frac{5*S}{8};$$
5) $$S_{MNK}=2*\frac{5*S}{8}=\frac{109}{8}=\frac{5S}{4};$$
Задание 6073
В треугольнике АВС биссектриса АD делит сторону ВС на отрезки ВD и DС, причем ВD : DС = 3:2. На стороне АС выбрана точка Е такая, что биссектриса АD пересекает ВЕ в точке F и ВF : FЕ = 5 : 2. Найдите площадь четырехугольника FDCE, если площадь треугольника АВС равна 70 см2 .
1) По т. Менелая из $$\Delta ADC:$$
$$\frac{BF}{FE}*\frac{EA}{AC}*\frac{CD}{BD}=1\Rightarrow$$ $$\frac{EA}{AC}=\frac{2}{5}*\frac{3}{2}=\frac{3}{5}\Rightarrow \frac{AE}{EC}=\frac{3}{2}$$;
2) по т. Менелая $$\Delta BEC$$:
$$\frac{AF}{FD}*\frac{DB}{BC}*\frac{CE}{EA}=1\Rightarrow \frac{AF}{FD}=\frac{5}{3}*\frac{3}{2}=\frac{5}{2}$$
3) $$S_{ADC}= \frac{DC}{BC}; S_{ABC}=\frac{2}{5}*70=28$$
4) $$\frac{S_{AFE}}{S_{ADC}}=\frac{AF*AE}{AD*AC}=\frac{\frac{5}{7}AD*\frac{3}{5}AC}{AD*AC}=\frac{3}{7}$$, тогда $$S_{FDCE}=\frac{4}{7}*S_{ADC}=\frac{4}{7}*28=16$$
Задание 6405
В остроугольном треугольнике АВС на высоте AD взята точка М, а на высоте ВР – точка N так, что углы ВМС и АNС – прямые. Расстояние между точками М и N равно $$4+2\sqrt{3}$$ , $$\angle MCN = 30$$. Найдите биссектрису СL треугольника CMN
1) $$\angle APB=\angle ADB=90$$ ,т.к. опирается на AB, то $$A_{1},B_{1},D_{1},P_{1}$$ лежат на одной окружности .
2) $$\angle PDA =\angle PBA$$ (вписаные , на одну дугу)
$$\angle A=90-\angle PBA(\Delta PBA)$$
$$\angle PDC=90-\angle PDA(\Delta ADC)$$
Тогда $$\angle A=\angle PDC$$, и т.к. $$\angle C$$ - общий , то $$\Delta ABC\sim \Delta PDC\Rightarrow$$ $$\frac{CB}{CP}=\frac{AC}{CD}\Leftrightarrow$$ $$AC*CP=BC*CD(1)$$
3) из $$\Delta ACN :CN^{2}=AC*CP$$
Из $$\Delta CMB: CM^{2}=BC*CD$$
С учетом (1): $$CN^{2}=CM^{2}\Rightarrow$$ $$CN=CM$$ и $$\Delta CMP$$ равнобедренный
4) Пусть CH- биссектриса , она и медиана и высота . $$NH=\frac{1}{2} NM=2+\sqrt{3}$$
$$\angle HCN=\frac{1}{2}\angle MCN=15$$
Из $$\Delta CHN \frac{HN}{HC}=tg \angle HCN\Rightarrow$$ $$HC=\frac{2+\sqrt{3}}{tg 15}$$
$$tg 15=\frac{\sin 30}{1+\cos 30}=\frac{1}{2+\sqrt{3}}$$
$$HC=(2+\sqrt{3})^{2}=7+4\sqrt{3}$$
Задание 6554
В треугольнике КЕМ длина стороны КЕ равна 27, длина биссектрисы КВ равна 24, а длина отрезка МВ равна 8. Найдите периметр треугольника КМВ.
1) Пусть KE=a=27; KM=b; EB=x; BM=y=8; KB=m=24; $$\angle EKB=\angle BKM=\alpha$$
2) По свойству биссектрисы: $$\frac{x}{y}=\frac{a}{b}(1)$$
3) Рассмотрим теорему косинусов для $$\Delta EBK$$ и $$\Delta BMK$$:
$$\left\{\begin{matrix}y^{2}=m^{2}+b^{2}-2mb \cos \alpha\\x^{2}=m^{2}+a^{2}-2ma \cos \alpha\end{matrix}\right.$$
Умножим первое и второе уравнения на a и b соответственно и вычтем из первого второе :
$$\left\{\begin{matrix}y^{2}a =m^{2}a+b^{2}a-2mab \cos \alpha\\x^{2}b=m^{2}b+a^{2}b-2mab \cos \alpha\end{matrix}\right.$$
Получим: $$y^{2}a-x^{2}b=m^{2}a+b^{2}a-m^{2}b-a^{2}b$$
Рассмотрим левую часть равенства: $$y^{2}a-x^{2}b=xy(\frac{ya}{x}-\frac{xb}{y})$$ .С учетом , что $$\frac{x}{y}=\frac{a}{b}$$, получим : $$xy(\frac{b}{a}*a-\frac{a}{b}*b)=xy(b-a).$$
Рассмотрим правую часть равенства: $$m^{2}a+b^{2}a-m^{2}b-a^{2}b=m^{2}(a-b)-ba(a-b)$$. Получим : $$xy(b-a)=m^{2}(a-b)-ba(a-b)$$.
Т.к. $$a\neq b$$ (иначе получим равнобедренный), то поделим $$a-b$$: $$-xy=m^{2}-ba\Rightarrow m^{2}=ab-xy(2)$$ - вообще, это формула длины биссектриссы через две стороны и отрезки третьей, но в учебниках за 7-9 класс ее не встречал, потому необходимо ее выводить.
4) Итого имеем систему: $$\left\{\begin{matrix}\frac{x}{y}=\frac{a}{b}\\m^{2}=ab-xy\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{x}{8}=\frac{27}{b}\\24^{2}=27b-8x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{216}{b}\\576=27b-\frac{8*216}{b}\end{matrix}\right.$$
$$576b=27b^{2}-1728\Leftrightarrow$$ $$27b^{2}-576b-1728=0|:9\Leftrightarrow$$ $$3b^{2}-64b-192=0$$
$$D=4096+2304=6400$$
$$b_{1}=\frac{64+80}{6}=\frac{144}{6}=24$$
$$b_{2}=\frac{64-80}{6}<0$$
5) $$P_{BMK}=m+y+b=24+8+24=56$$
Задание 6601
В равнобедренном треугольнике ABC (АВ = ВС) проведена биссектриса АМ. Известно, что ВС : МС = 5 : 2. Найдите отношение длины отрезка МС к радиусу окружности, описанной около треугольника АМС.
1) $$BC:MC =5:2\Rightarrow$$ $$BM:MC=3:2$$. Пусть $$BM=3y\Rightarrow$$ $$MC=2y, BC=5y$$
2) По свойству биссектрисы: $$\frac{AB}{AC}=\frac{BM}{MC}\Rightarrow$$ $$\frac{AB}{AC}=\frac{3}{2}$$. $$AB=BC=5y\Rightarrow$$ $$AC=\frac{5*2y}{3}=\frac{10y}{3}$$
3) $$AM=\sqrt{AB*AC-BM*MC}=$$$$\sqrt{5y*\frac{10y}{3}-3y*2y}=$$$$\sqrt{\frac{50y^{2}-12y^{2}}{3}}=$$$$\sqrt{\frac{32 y^{2}}{3}}=$$$$4y\sqrt{\frac{2}{3}}$$
4) $$S_{AMC}=S_{ABC}*\frac{MC}{BC}$$, $$p_{ABC}=5y+5y+\frac{10y}{3}=\frac{20y}{3}$$
$$S_{ABC}=\sqrt{\frac{20y}{3}*(\frac{20y}{3}-5y)^{2}(\frac{20y}{3}-\frac{10y}{3})}=$$$$\frac{50y^{2}\sqrt{2}}{9}\Rightarrow$$
$$S_{AMC}=\frac{2}{5}*\frac{50y^{2}\sqrt{2}}{9}=$$$$\frac{20y^{2}\sqrt{2}}{9}$$
5) $$R=\frac{MC*AC}{4 S_{AMC}}\Rightarrow$$ $$\frac{MC}{R}=\frac{4 S_{AMC}}{AM*AC}=$$$$\frac{4*20y^{2}\sqrt{2}}{9}:(4y\frac{\sqrt{2}}{\sqrt{3}}*\frac{10y}{3})=$$$$\frac{2\sqrt{3}}{3}$$
Задание 7005
В треугольнике АВС площадью 90 см2 биссектриса AD делит сторону ВС на отрезки BD и CD, причём BD : CD = 2 : 3. Отрезок BL пересекает биссектрису AD в точке Е и делит сторону АС на отрезки AL и CL такие, что AL : CL = 1 : 2. Найдите площадь четырёхугольника EDCL.
Пусть $$AL=y\Rightarrow$$ $$LC=2y; AC=3y$$
1) $$S)_{ABC}=90$$; $$\frac{S_{ABD}}{S_{ADC}}=\frac{BD}{DC}=\frac{2}{3}\Rightarrow$$ $$S_{ABD}=\frac{2}{5}S_{ABC}=36$$. $$S_{ADC}=\frac{3}{5}S_{ABC}=54$$
2) Пусть $$DK\left | \right |EL \Rightarrow$$ по т. Фалеса : $$\frac{CK}{KL}=\frac{CD}{DB}=\frac{3}{2}\Rightarrow$$$$CK=\frac{3}{5}CL=\frac{6}{5}y$$. $$KL=\frac{2}{5}CL=\frac{4}{5}y$$
3) По т. Фалеса для $$\angle DAC$$: $$\frac{AE}{ED}=\frac{AL}{LK}=$$$$\frac{y}{0,8 y}=\frac{5}{4}\Rightarrow$$ $$AE=\frac{5}{9}AD$$
4) $$\frac{S_{AEL}}{S_{ADC}}=\frac{AE*AL}{AD*AC}=\frac{5}{27}\Rightarrow$$ $$S_{DELC}=\frac{22}{27}S_{ADC}=44$$
Задание 7091
Дан треугольник АВС, на стороне АС взята точка Е так, что АЕ : ЕС = 2: 3 , а на стороне АВ взята точка D так, что АD : DB = 1: 4 . Проведены отрезки СD и ВЕ. Найдите отношение площади получившегося четырехугольника к площади данного треугольника.
1) $$BE\cap CD=H$$ ; Пусть $$AE=2x$$ ; $$AD=y \Rightarrow$$ $$DB=4y; EC=3x$$
2) Построим $$DK\left | \right |BE (K=DK\cap AC)\Rightarrow$$ по т Фалеса : $$\frac{AD}{DB}=\frac{AK}{KE}\Rightarrow$$ $$AK=0,4 x; KE=1,6 x$$.
3) Пусть $$S_{ABC}=S$$; $$S_{ADC}=\frac{AD}{AB}S=\frac{S}{5}$$; $$S_{ADK}=\frac{AK}{AC}S_{ADC}=$$$$\frac{2}{25}*\frac{S}{5}=\frac{2S}{125};$$
4) $$HE\left | \right | DK \Rightarrow$$ $$\Delta CHE\sim \Delta CDK$$; $$\frac{S_{CHE}}{S_{CDK}}=(\frac{CE}{CK})^{2}=$$$$(\frac{15}{23})^{2}=\frac{225}{529}\Rightarrow$$ $$S_{DHEK}=\frac{529-225}{529}*S_{CDK}$$; $$S_{CDK}=S_{ADC}-S_{ADK}=\frac{23S}{125}$$; $$S_{DHEK}=\frac{304}{529}*\frac{23S}{125}=\frac{304 S}{23*125}$$; $$S_{ADHE}=\frac{2S}{125}+\frac{304 S}{23*125}=\frac{350 S}{23*125}=\frac{14 S}{115}\Rightarrow$$ $$\frac{S_{ADHE}}{S_{ABC}}=\frac{14}{115}$$
Задание 7254
В треугольнике ABC биссектрисы AD и BE пересекаются в точке О. Найдите отношение площади четырехугольника DOEC к площади треугольника ABC, если AC:AB:BC = 4:3:2.
1) Пусть $$AC=4x; AB=3x;BC=2x$$.
2) По свойству биссектрисы $$\frac{AB}{AC}=\frac{BD}{DC}=\frac{3}{4}\Rightarrow$$ $$BD=\frac{3}{7}BC=\frac{6x}{7}$$; $$DC=\frac{4}{7}BC=\frac{8x}{7}$$. Аналогично, $$\frac{AB}{BC}=\frac{AE}{EC}=\frac{3}{2}\Rightarrow$$ $$AE=\frac{3}{5}AC=\frac{12x}{5}$$; $$EC=\frac{2}{5}AC=\frac{8x}{5}$$
3) Пусть $$EH\left | \right |OD\Rightarrow$$ по т. Фалеса : $$\frac{AE}{EC}=\frac{DH}{HC}=\frac{3}{2}\Rightarrow$$ $$DH=\frac{3}{5} DC=\frac{24x}{35}$$$$\Rightarrow$$ $$BH=\frac{54x}{35}$$
4)Пусть $$S_{ABCD}=S$$ $$\Rightarrow$$ при этом $$S_{BEC}=\frac{EC}{AC}S=\frac{2}{5}S$$; $$S_{BEH}=\frac{BH}{BC}S_{BEC}=$$$$\frac{54}{70}*\frac{2}{5}S=\frac{54S}{175}$$
5) т.к. $$OD\left | \right |EH$$, то $$\frac{S_{OBD}}{S_{BEH}}=(\frac{BD}{BH})^{2}=\frac{25}{81}$$ $$\Rightarrow$$ $$\frac{2 S}{3*7}=\frac{2S}{21}\Rightarrow$$ $$S_{DOEC}=S_{BEC}-S_{OBD}=$$$$\frac{2}{5}S-\frac{2S}{21}=\frac{32 S}{105}\Rightarrow$$$$ \frac{S_{DOEC}}{S_{ABC}}=\frac{32}{105}$$
Задание 8975
Стороны AC, AB, BC треугольника ABC равны $$2\sqrt{5}$$, $$\sqrt{13}$$, 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает отрезок AB в точке, отличной от B. Известно, что треугольник с вершинами A, K, C подобен исходному. Найдите косинус угла AKC, если известно, что $$\angle KAC=90$$.
Задание 10985
В треугольнике АВС на его медиане ВМ отмечена точка К так, что $$ВК : КМ = 6 : 7$$. Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади треугольника ВКР к площади треугольника АВК.
1)$$S_{ABM}=\frac{S_{ABC}}{2}=0,5S$$ (тогда BM - медиана)
2)$$\frac{S_{ABK}}{S_{AKM}}=\frac{BK}{KM}=\frac{6}{7}$$ (общая вершина) $$\to S_{ABK}=\frac{6}{13}S_{ABM}=\frac{3S}{13}.$$
3) Пусть $$ML\parallel KP\to \frac{BP}{PL}=\frac{BK}{KM}=\frac{6}{7}$$. Но $$\frac{PL}{LC}=\frac{AM}{MC}=\frac{1}{1}\to BP:PL:LC=6:7:7$$. Тогда $$\frac{S_{ABP}}{S_{ABC}}=\frac{BP}{BC}=\frac{6}{20}\to S_{ABP}=\frac{3}{10}S;$$ $$S_{BKP}=\frac{3S}{10}-\frac{3S}{13}=\frac{(39-30)S}{130}=\frac{9S}{130}\to \frac{S_{BKP}}{S_{ABK}}=\frac{9S}{130}\cdot \frac{13}{3S}=\frac{3}{10}$$
Задание 11047
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника AKM к площади четырехугольника KPCM.
1) Пусть $$S_{ABC}=S\to S_{ABM}=S_{BMC}=\frac{S}{2}.$$
2) $$\frac{S_{ABK}}{S_{AKM}}=\frac{BK}{KM}=\frac{4}{9}\to S_{AKM}=\frac{9}{13}S_{ABM}\frac{9}{13}\cdot \frac{S}{2}=\frac{9S}{26}.$$
3) Пусть $$ML\parallel AP\to ML$$ - средняя линия $$\triangle APL$$ и $$PL=LC.$$ Но $$KP\parallel ML\to \frac{BK}{KM}=\frac{BP}{PL}=\frac{4}{9},$$ тогда $$\frac{BP}{PC}=\frac{4}{18}.$$
4) $$\frac{S_{APC}}{S_{ABC}}=\frac{PC}{BC}=\frac{18}{22}\to S_{APC}=\frac{9}{11}S\to S_{KPOM}=S_{APC}-S_{AKM}=\frac{9S}{11}-\frac{9S}{26}=$$ $$=\frac{9S(26-11)}{26\cdot 11}=\frac{15\cdot 9S}{26\cdot 11}\to \frac{S_{AKM}}{S_{KPCM}}=\frac{9}{26}\cdot \frac{26\cdot 11}{15\cdot 9}=\frac{11}{15}.$$
