ОГЭ
Задание 1985
Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
- Пусть a - сторона ромба, тогда $$a=\frac{40}{4}=10$$
- Найдем площадь ромба: $$S=10*10*\sin 30^{\circ}=50$$
Задание 1986
Периметр ромба равен 24, а синус одного из углов равен $$\frac{1}{3}$$. Найдите площадь ромба.
- Пусть a - сторона ромба, тогда $$a=\frac{24}{4}=6$$
- Найдем площадь ромба: $$S=6*6*\frac{1}{3}=12$$
Задание 1987
Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Из формулы площади параллелограмма: $$S=12*10=120$$
Задание 1988
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на $$\sqrt{2}$$.
Из формулы площади параллелограмма: $$S=12*5*\sin 45=30\sqrt{2}$$. В ответе необходимо найти указать ответ, деленный на $$\sqrt{2}$$, то есть 30
Задание 1990
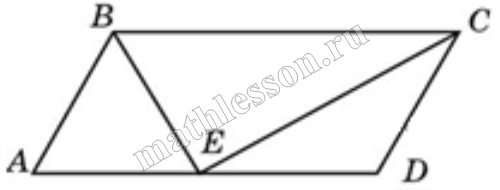
Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
- Найдем площадь треугольника AED: $$S_{AED}=\frac{1}{2}ED*h=\frac{1}{4}CD*h=\frac{1}{4}S_{ABCD}$$, где h - высота параллелограмма
- Тогда $$S_{AECB}=\frac{3}{4}S_{ABCD}=42$$
Задание 1991
Найдите площадь ромба, если его диагонали равны 14 и 6.
Из формулы площади ромба: $$S=\frac{1}{2}*14*6=42$$
Задание 1992
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.

- Из треугольника AED: $$S_{AED}=\frac{1}{2}*1*9=4,5$$
- Ромб состоит из четырех равных прямоугольных треугольников, образованных диагоналями ромба, тогда $$S_{ABCD}=4S_{AED}=18$$