ОГЭ
Задание 6119
Середины сторон параллелограмма являются вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
- $$AB=CD, BC=AD$$ так как дан параллелограмм. Следовательно, $$AM=MB=DL=LC$$, и $$AK=KD=BN=NC$$.
- $$\angle A+\angle D=180$$. Но $$MK=NK$$, следовательно, треугольники AMK и KLD равны по трем сторонам и $$\angle A=\angle D$$. Так как они в сумме дают 180, то какждый из них по 90, тогда ABCD - прямоугольник.
Задание 6167
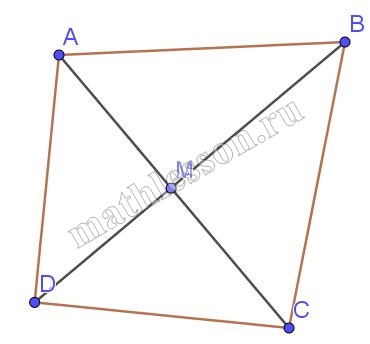
В выпуклом четырёхугольнике АВСD углы ACB и ADB равны. Докажите, что углы ABD и ACD также равны.
1) $$\angle AMD=\angle BMC$$(вертикальные) $$\angle ADB=\angle ACB$$(по условию) $$\Rightarrow \Delta AMB \sim \Delta BMC$$ и $$\frac{AM}{MB}=\frac{MD}{MC}(1)$$
2) $$\angle AMB=\angle DMC$$ (вертикальные) с учетом равенства (1) получим $$\Delta AMB \sim \Delta DMC\Rightarrow \angle ABD=\angle ACD$$
Задание 6214
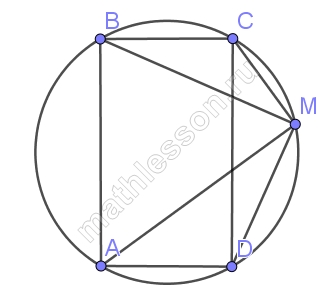
Точка М лежит на окружности радиуса R, описанной около прямоугольника ABCD. Докажите, что МА2 + МВ2 + МС2 + МD2 = 8R2
- $$\angle CMA=90$$, AC-диаметр окружности . Тогда из $$\Delta ACM$$
- $$AC^{2}=MC^{2}+MA^{2}\Leftrightarrow (2R)^{2}=MC^{2}+MA^{2}(1)$$
- Аналогично , из $$\Delta BMD: (2R)^{2}=MB^{2}+MD^{2}(2)$$
- Сложим (1)и(2): $$MA^{2}+MB^{2}+MC^{2}+MD^{2}=8R^{2}$$
Задание 6310
На основаниях АВ и СD вне трапеции построены квадраты. Докажите, что прямая, соединяющая их центры, проходит через точку пересечения диагоналей трапеции.
Пусть $$K\in B_{1}C$$, $$O=BD\cap AC$$, $$M=KO\cap AD$$
1) $$\angle LCK=\angle MAN=45$$; $$\angle LCO=\angle OAN$$(накрест лежащие) $$\Rightarrow \angle KCA=\angle OAD_{1}\Rightarrow$$ $$CB_{1}\left | \right |AD_{1}$$
2) $$\angle LKC=\angle NMA$$(накрест лежащие) $$\Rightarrow \Delta KLC\sim \Delta ANM\Rightarrow$$ $$\frac{KC}{AM}=\frac{CL}{AN}=k$$
3) $$LC\left | \right |AN\Rightarrow$$ $$\Delta LCO\sim \Delta ONA\Rightarrow$$ $$\frac{LC}{AN}=\frac{LO}{ON}=k$$
4) $$LC\left | \right |AN \Rightarrow$$ $$\Delta BLO\sim \Delta OND\Rightarrow$$ $$\frac{LO}{ON}=\frac{BL}{ND}=k$$
5)т.к. $$\frac{LC}{AN}=k$$, $$\frac{BL}{ND}=k$$ $$\Rightarrow \frac{BC}{AD}=k$$,но $$\frac{KC}{AM}=k$$ и $$\angle KCL=\angle MAN\Rightarrow$$ $$\Delta KCB\sim \Delta ADC$$ и если K-центр , то и М-центр
Задание 6404
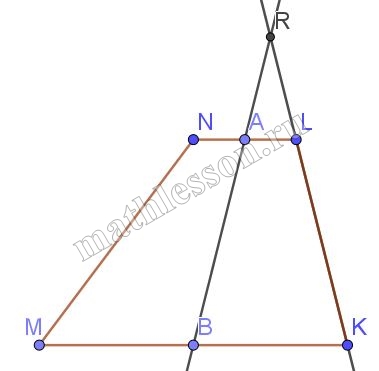
На одной из параллельных сторон трапеции взята точка А, на другой – точка В. Докажите, что отрезок АВ делится средней линией трапеции пополам.
1) Достроим $$BA\cap KL=R$$. $$\Delta ARL\sim \Delta RHH\sim \Delta BRK$$ ( т.к. $$AL\left | \right |HP\left | \right | BK$$)
2) По т. Фелеса : $$RL:LP:PK=AR: AH: HB \Rightarrow$$ $$LP :PK =1:1\Rightarrow AH: HB= 1 :1$$