ОГЭ
Задание 6451
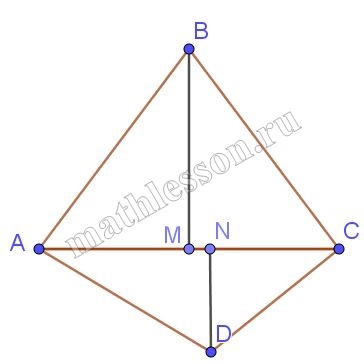
В выпуклом четырёхугольнике ABCD противоположные углы А и С прямые. На диагональ АС опущены перпендикуляры ВМ и DN. Докажите, что СМ = NA.
1) Пусть $$\angle ABM=\alpha$$, тогда из $$\Delta ABM: \angle BAM=90-\alpha$$ , тогда $$\angle MAD=\alpha$$ и из $$\Delta ADH:$$$$\angle ADN =90-\alpha \Rightarrow$$ $$\Delta ABM\sim \Delta AND$$, тогда : $$\frac{DH}{AM}=\frac{AN}{BM}\Rightarrow$$ $$DN*BM=AM*AN(1)$$
2) Аналогично $$\Delta BMC\sim \Delta CHD$$ и $$\frac{DH}{CM}=\frac{NC}{BM}\Rightarrow$$ $$DN*BM=CM*NC(2)$$
3) С учетом (1) и (2): $$AM *AN=CM*NC$$ или $$AM(AM+MN)=CN(CN+MN)\Leftrightarrow$$ $$AM^{2}+AM*MN=CN^{2}+CN*MN\Leftrightarrow$$ $$AM^{2}-CN^{2}+AM*MN-CN*MN=0\Leftrightarrow$$ $$(AM-CN)(AM+CN)+MN(AM-CN)=0\Leftrightarrow$$ $$(AM-CN)(AM+CN+MN)=0$$. $$AM+CN+MN>0$$ всегда, следовательно, $$AM-CN=0$$ или $$AM=CN$$
Задание 6553
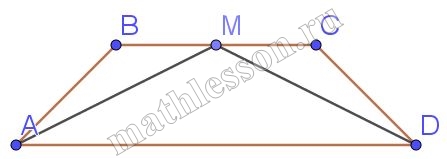
Биссектрисы углов А и D равнобедренной трапеции АВСD пересекаются в точке М стороны ВС. Докажите, что М – середина ВС.
1) $$\angle A=\angle D\Rightarrow$$ $$\angle BAM=\angle MDC$$
2) $$\angle BAM=\angle MAD$$(AM-биссектриса ); $$\angle MAD=\angle BMA$$(накрест лежащие) $$\Rightarrow \angle BAM=\angle BMA\Rightarrow$$ $$\Delta ABM$$ - равнобедренный
3)Аналогично $$\Delta MCD$$ - равнобедренный $$\Rightarrow$$ $$AB=BM; MC=CD$$, но $$AB=CD\Rightarrow BM=MO$$
Задание 6600
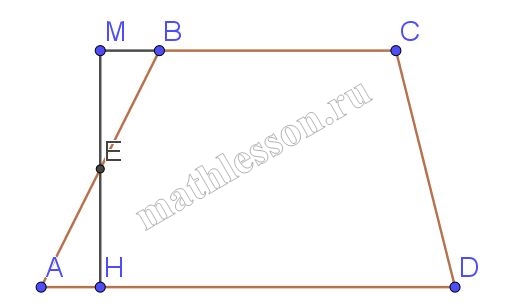
Пусть Е – середина стороны АВ трапеции АВСD (ВС ॥ АD). Докажите, что площадь треугольника ЕСD равна половине площади трапеции АВСD.
- Пусть $$EH\perp AD; EH=h$$
- $$\Delta EMD=\Delta EHA$$(по гипотенузе и острому углу )$$\Rightarrow$$ $$EM=h\Rightarrow$$ $$MH=2h$$
- Пусть $$BC=x; AD=y$$: $$S_{ABCD}=\frac{x+y}{2}*2h=xh+yh$$, $$S_{EBC}=\frac{1}{2}hx$$, $$S_{EAD}=\frac{1}{2}hy\Rightarrow$$ $$S_{CED}=h(x+y)-\frac{1}{2}h(x+y)=$$$$\frac{1}{2}h(x+y)=\frac{S_{ABCD}}{2}$$
Задание 6648
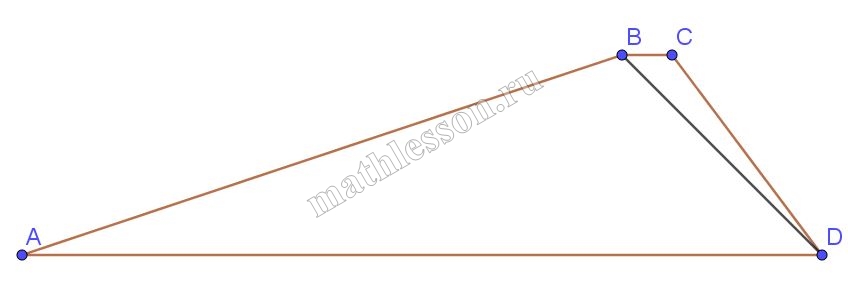
Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и BDA подобны.
1) $$\angle CBD=\angle BDA$$(накрест лежащие)
2) $$\frac{BD}{AD}=\frac{BC}{BD}$$. С учетом п.1 получим, что $$\Delta BCD\sim \Delta BDA$$
Задание 6789
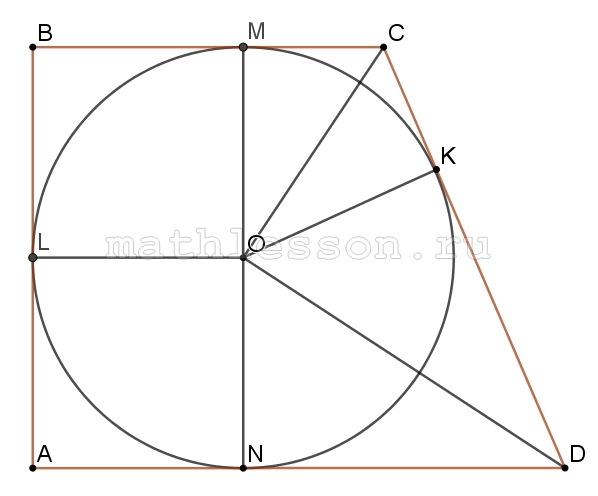
Докажите, что площадь прямоугольной трапеции, в которую можно вписать окружность, равна произведению длин её оснований.
1) т.к. можно вписать окружность , то $$AB+CD=BC+AD$$
2) $$S_{ABCD}=\frac{BC+AD}{2}*MN$$
Пусть $$OK\perp CD$$(OK-радиусы) . По свойству касательных : $$MC=CK$$, $$OM\perp CD\Rightarrow$$ $$\Delta MCO=\Delta CKO$$(по катету и гипотенузе) , аналогично, $$\Delta OKD=\Delta ODN$$. Тогда: $$\angle KDO=\angle ODN=\frac{\angle D}{2}=\frac{\alpha }{2}$$ и $$\angle MCO=\angle OCK=\frac{\angle C}{2}=\frac{180-\alpha }{2}=90-\frac{\alpha }{2}$$
Тогда: $$\angle COD=180-\frac{\alpha }{2}-(90-\frac{\alpha }{2})=90\Rightarrow$$ $$OK=\sqrt{CK*KD}$$.
Пусть CK=a, KD=b, OK=r, тогда: OL=OM=r; BM=BL; $$\angle B=90\Rightarrow$$ $$BM=BL=r$$; $$r^{2}=ab$$, $$BC=BM+MC=r+a$$, $$AD=AN+ND=r+b$$, $$AB=2r$$
3) $$S=\frac{r+a+r+b}{2}*2r=$$$$(2r+a+b)*2=2r^{2}+ar+br=$$$$r^{2}+r^{2}+ar+br=$$$$r^{2}+ab+ar+br=$$$$r(r+b)+a(r+b)=(r+b)(r+a)=AD*BC$$
Задание 6860
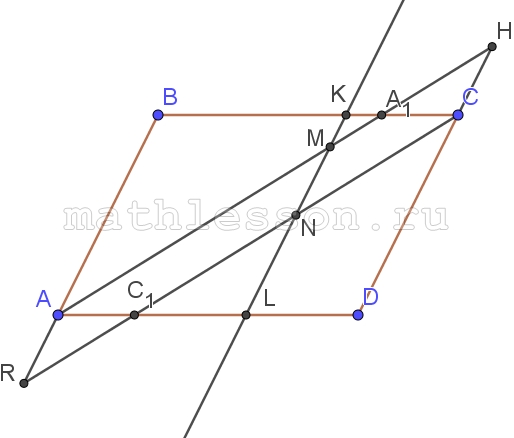
Дан параллелограмм ABCD. Прямая, параллельная AB, пересекает биссектрисы углов A и C в точках M и N соответственно. Докажите, что углы ADM и ABN равны
Биссектрисы $$AA_{1}$$ и $$CC_{1}$$; $$AA_{1}\cap CD=H$$; $$CC_{1}\cap AB=R$$
1) Пусть $$\angle A=2\alpha$$ $$\Rightarrow$$ $$\angle BAA_{1}=\angle A_{1}AD=$$$$\angle BCC_{1}=\angle C_{1}CD=\alpha $$($$AA_{1}; CC_{1}$$ - биссектрисы)
2) $$\angle AHC=\angle BAA_{1}=\alpha$$ ; $$\angle ARC=\angle C_{1}CR=\alpha$$ (накрест лежащие ) $$\Rightarrow$$ $$BC=AD$$, то равнобедренные $$\Delta RBC=\Delta AHD$$$$\Rightarrow$$ $$RB=AD(1)$$
3) $$\angle BAM=\angle BRN=\alpha$$ $$\Rightarrow$$ $$AM\left | \right |RN, AR\left | \right |NM$$ (по построению ) $$\Rightarrow$$ AMNR - параллелограмм $$\Rightarrow$$ $$RN=AM(2)$$
4)С учетом (1) и (2) , и, что $$\angle BRN =\angle MAD=\alpha$$ $$\Rightarrow$$ $$\Delta BRN=\Delta MAD$$$$\Rightarrow$$ $$\angle ABN=\angle ADM$$
Задание 6956
На стороне BC квадрата ABCD взята точка Р. Докажите, что площадь квадрата вдвое больше площади треугольника AРD.
1) Пусть $$PH\mid AD\Rightarrow$$ $$PHDC$$ - прямоугольник $$\Rightarrow$$ $$PH=CD$$
2) $$S_{ABCD}=AB*BC$$; $$S_{ABCD}=\frac{1}{2}*AD*PH$$; $$PH=CD=AB$$; $$AD=BC\Rightarrow$$ $$S_{ABCD}=\frac{1}{2} *AB*BC=\frac{1}{2} S_{ABCD}$$
Задание 7004
Четырехугольник ABCD таков, что около него можно описать окружность и в него можно вписать окружность. Разность длин сторон AD и BC равна разности сторон АВ и СD. Докажите, что диагональ АС – диаметр описанной окружности.
1) Т.к. можно вписать в него окружность , то $$AB+CD=BC+AD (1)$$. По условию $$AD-BC=AB-CD (2)$$
2) Пусть $$\angle A=\alpha$$ , тогда $$\angle C=180-\alpha$$ (т.к. можно выслать окружность)
Тогда $$\angle B=90-\frac{\alpha }{2}+\frac{\alpha }{2}=90\Rightarrow$$ AC-диаметр
Задание 7472
Биссектрисы углов B и C трапеции ABCD пересекаются в точке О, лежащей на стороне AD. Докажите, что точка О равноудалена от прямых АВ, ВС и CD
1) Пусть OH, OM и OK - расстояния до AB, BC и CD соответственно.
2) Для угла ABC: OH=OM по свойству биссектрисы. Аналогично для угла DCB: OK=OM. Следовательно, OH=OK=OM