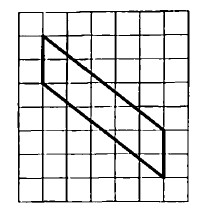
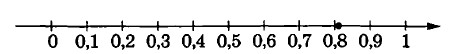ОГЭ 2023. Вариант 9 Ященко 36 вариантов ФИПИ школе.



Решаем 9 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 9 варианта (всех заданий).

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Аналоги к этому заданию:

Задания 1-5

Общепринятые форматы листов бумаги обозначают буквой $$A$$ и цифрой: $$A0$$, $$A1$$, $$A2$$ и так далее. Площадь листа формата $$A0$$ равна 1 кв. м. Если лист формата $$A0$$ разрезать пополам параллельно меньшей стороне, получаются два листа формата $$A1$$.

​​Если так же лист $$A1$$ разрезать пополам, получаются два листа формата $$A2$$ и так далее.

Отношение длины листа к его ширине у всех форматов, обозначенных буквой $$A$$, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится). На практике размеры листа округляются до целого числа миллиметров.

В таблице 1 даны размеры листов бумаги четырёх форматов: от $$A3$$ до $$A6$$.

порядковые номера ширина (мм) длина (мм)
1 105 148
2 210 297
3 297 420
4 148 210

1. Для листов бумаги форматов $$A3$$, $$A4$$, $$A5$$ и $$A6$$ определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.

формат бумаги А3 А4 А5 А6
порядковые номера        

2. Сколько листов бумаги формата $$A5$$ получится при разрезании одного листа бумаги формата $$A0$$?

3. Найдите длину большей стороны листа бумаги формата $$A2$$. Ответ дайте в миллиметрах.

4. Найдите площадь листа бумаги формата $$A3$$. Ответ дайте в квадратных сантиметрах.

5. Бумагу формата $$A5$$ упаковали в пачки по $$500$$ листов. Найдите массу пачки, если масса бумаги площадью 1 кв. м равна 80 г. Ответ дайте в граммах.

Ответ: 1)3241 2)32 3)594 4)1247,4; 1250 5)1250
Решение 1 Решение 2 Решение 3 Решение 4 Решение 5 Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 6

Найдите значение выражения $$-0,3\cdot(-10)^{4}+4\cdot(-10)^{2}-59$$
Ответ: -2659
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 7

Одно из чисел $$\frac{4}{11}$$; $$\frac{8}{11}$$; $$\frac{9}{11}$$; $$\frac{13}{11}$$ отмечено на прямой точкой.

Какое это число?

  1. $$\frac{4}{11}$$;
  2. $$\frac{8}{11}$$;
  3. $$\frac{9}{11}$$;
  4. $$\frac{13}{11}$$
Ответ: 3
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 8

Найдите значение выражения $$\frac{(3\cdot 8)^{7}}{3^{7}\cdot 8^{5}}$$
Ответ: 64
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 9

Решите уравнение $$5x^{2}-8x=0$$. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Ответ: 1,6
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 10

В каждой двадцатой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Аля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Аля не найдёт приз в своей банке.
Ответ: 0,95
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 11

Установите соответствие между формулами, которыми заданы функции, и их графиками.

ФОРМУЛЫ

  1. $$y=-x^{2}-5x-2$$;
  2. $$y=-\frac{1}{3x}$$;
  3. $$y=-\frac{1}{6}x-4$$

ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.

А Б В
     

 

Ответ: 312
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 12

Площадь треугольника можно вычислить по формуле$$S=\frac{abc}{4R}$$, где $$a$$, $$b$$, $$c$$ — стороны треугольника, a $$R$$ — радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите $$b$$, если $$a=13$$, $$c=15$$, $$S=84$$ и $$R=\frac{65}{8}$$.
Ответ: 14
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 13

Укажите неравенство, которое не имеет решений.

  1. $$x^{2}+78>0$$;
  2. $$x^{2}+78<0$$;
  3. $$x^{2}-78>0$$;
  4. $$x^{2}-78<0$$
Ответ: 2
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 14

Известно, что на высоте 2205 м над уровнем моря атмосферное давление составляет $$550$$ мм рт. ст. Считая, что при подъёме на каждые $$10,5$$ м давление уменьшается примерно на 1 мм рт. ст., определите атмосферное давление на высоте $$2520$$ м над уровнем моря.
Ответ: 520
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 15

На гипотенузу $$AB$$ прямоугольного треугольника $$ABC$$ опущена высота $$CH$$, $$AH=7$$, $$BH=28$$. Найдите $$CH$$.
Ответ: 14
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 16

Радиус окружности, вписанной в равносторонний треугольник, равен $$15$$. Найдите высоту этого треугольника.
Ответ: 45
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 17

Основания трапеции равны $$5$$ и $$9$$. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Ответ: 4,5
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 18

На клетчатой бумаге с размером клетки $$1*1$$ изображён параллелограмм. Найдите его площадь.

Ответ: 10
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 19

Какие из следующих утверждений верны?

  1. Существует квадрат, который не является прямоугольником.
  2. Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
  3. Все диаметры окружности равны между собой.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Ответ: 23
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 20

Решите уравнение $$(x^{2}-25)^{2}+(x^2+2x-15)^{2}=0$$

Ответ: -5
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 21

Первую половину пути автомобиль проехал со скоростью $$34$$ км/ч, а вторую — со скоростью $$51$$ км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Ответ: 40,8 км/ч
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 22

Постройте график функции $$=x|x|+2|x|-3x$$. Определите, при каких значениях $$m$$ прямая $$y=m$$ имеет с графиком ровно две общие точки.
Ответ: -0,25;6,25
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 23

Точка Н является основанием высоты $$BH$$, проведённой из вершины прямого угла $$B$$ прямоугольного треугольника $$ABC$$. Окружность с диаметром $$BH$$ пересекает стороны $$AB$$ и $$CB$$ в точках $$P$$ и $$K$$ соответственно. Найдите $$BH$$, если $$PK=12$$.
Ответ: 12
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 24

Точка $$M$$ — середина боковой стороны $$AB$$ трапеции $$ABCD$$, а $$MC=MD$$. Докажите, что трапеция $$ABCD$$ прямоугольная.
Ответ: ч.т.д.
Видео-решение Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 25

Середина $$M$$ стороны $$AD$$ выпуклого четырёхугольника $$ABCD$$ равноудалена от всех его вершин. Найдите $$AD$$, если $$BC=18$$, а углы $$B$$ и $$C$$ четырёхугольника равны соответственно $$132^{\circ}$$ и $$93^{\circ}$$.
Ответ: $$18\sqrt{2}$$
Видео-решение Предложить свое решение / сообщить об ошибке