ОГЭ 2023. Вариант 2 Ященко 36 вариантов ФИПИ школе.
Решаем 2 вариант ОГЭ Ященко 2023 года сборника ФИПИ школе 36 вариантов. Полный разбор всего 2 варианта (всех заданий).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задания 1-5
Глеб Сергеевич начал строить на дачном участке теплицу длиной 5 метров (DC на рис. 1). Для этого он сделал прямоугольный фундамент (рис. 2). Для каркаса теплицы нужно заказать металлические дуги в форме полуокружностей длиной 6 м каждая и покрытие для обтяжки теплицы. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рис. 1 прямоугольником EFKN, где точки Е, Р и делят отрезок AD на равные части. Внутри теплицы Глеб Сергеевич планирует сделать три грядки, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20 х 20 см.
- Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
- Найдите ширину теплицы в метрах с точностью до десятых.
- Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 8 штук?
- Найдите площадь участка внутри теплицы, отведённого под грядки, в квадратных метрах. Результат округлите до десятых.
- Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого.
Задание 12
Площадь четырёхугольника можно вычислить по формуле $$S=\frac{d_{1}d_{2}\sin\alpha}{2}$$, $$d_{1},d_{2}$$ - длины диагоналей четырёхугольника, $$\alpha$$ - угол между диагоналями. Пользуясь этой формулой найдите длину диагонали $$d_{2}$$, если $$d_{1}=9$$, $$\sin\alpha=\frac{5}{8}$$, $$S=56,25$$
Задание 17
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
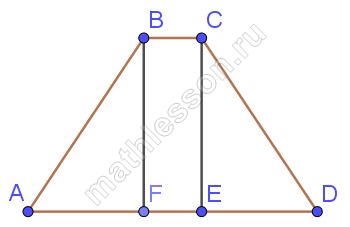
- Опустим высоты CE и BF. Тогда FE=BC=3, $$AF=ED=\frac{AD-FE}{2}=3$$ (из равенства прямоугольных треугольников ABF и CED)
- Пусть $$\angle D=45^{\circ}$$, тогда треугольник CED - равнобедренный ($$\angle ECD=90-45=45=\angle D$$), тогда CE=ED=3
- Из формулы площади трапеции: $$S_{ABCD}=\frac{3+9}{2}*3=18$$
Задание 19
Какое из следующих утверждений верно?
- Любой параллелограмм можно вписать в окружность.
- Сумма острых углов прямоугольного треугольника равно 90 градусам.
- Касательная к окружности параллельна радиусу, проведенному в точку касания.
В ответ запишите номер выбранного утверждения.
Задание 21
Первый велосипедист выехал из посёлка по шоссе со скоростью 24 км/ч. Через час после него со скоростью 21 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часа после этого догнал первого.