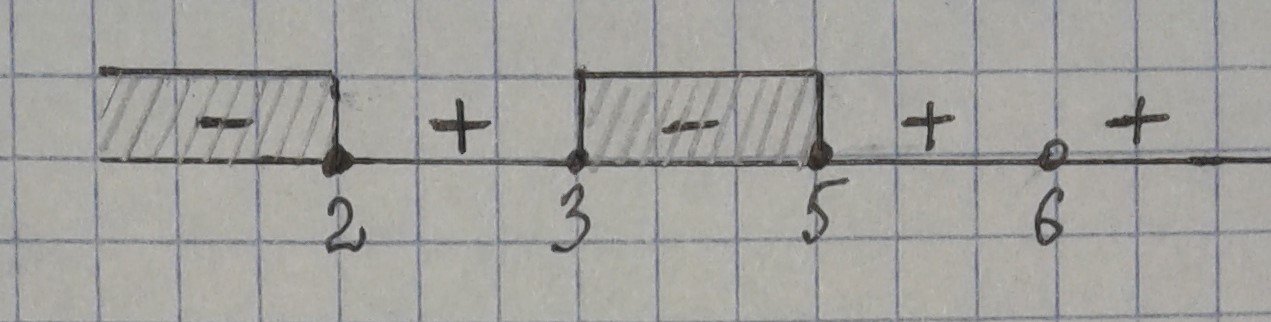Вопрос 2. Правильно ли решено дробно-рациональное неравенство?

Ученик решение неравенства $$\frac{(5-x)(x-3)(x-2)(x^2-x+6)}{(x-6)^2}\geq 0$$ приводит такие суждения: $$x^2-x+6=0$$ $$D=1-24-$$ нет решений , $$\frac{(5-x)(x-3)(x-2)}{(x-6)^2}\geq 0$$. Далее пользуется методом интервалов, определяет знак выражений, находящихся в скобках. И делает вывод. Как Вы относитесь к такому решению?

(Учительница математики).

Мне трудно сказать, правильный ли ученик получает ответ. Я вижу вот что. Ученик стремится использовать так называемый обобщенный (классический) метод интервалов. (Он больше интересуется корнями конкретных сомножителей). Но очень хотелось бы, чтобы он выбрал все же более короткий путь. И пользовался методом интервалов, удобным для решения дробно-рациональных неравенств, а не неравенств, в котором содержатся трансцендентные функции (неалгебраические, такие, как показательные, логарифмические, тригонометрические).

На месте ученика я поступил бы так:

1) Замечаем, что квадратный трехчлен $$x^2-x+6>0$$ для любого действительного х. (Старшеклассникам это уже надо "видеть"). Сослаться на то, что $$D=1-24<0$$, конечно, можно, но не ради того, что установить, что квадратный трехчлен не имеет корней, а скорее всего, для того, чтобы установить: знак выражения $$x^2-x+6$$ положителен для любого $$x\in R.$$ Следовательно, разделив обе части неравенства на это выражение, получим неравенство равносильное предшествующему.

2) Считаем, что совершенно необходимо в числителе двучлен $$5-x$$ заменить двучленом $$x-5$$, изменив знак неравенства на противоположный.

3) Знаменатель положителен при любом значении $$x\in R,$$ за исключением $$x=6$$. Значит, при умножении обеих частей неравенства с учетом того, что $$x?6$$, мы получаем неравенство, равносильное ему предшествующему.

С учетом этих соображений решение исходного неравенства оформил бы так: $$\frac{(5-x)(x-3)(x-2)(x^2-x+6)}{(x-6)^2}?0$$. $$x^2-x+6>0$$ для любого $$x\in R.$$ $$x\neq 6.$$ $$\frac{(x-5)(x-3)(x-2)}{(x-6)^2}?0$$; $$\left\{ \begin{array}{c} x?6 \\ (x-5)(x-3)(x-2)?0 \end{array} \right.$$ . Далее используем метод интервалов.

Ответ: $$(-\infty;2],\left[3;5\right].$$

Замечания.

1) Автор этих строк стремился как-то войти в "образ" школьника. Поэтому логические связки не использованы. Они (связки) несут определенную логическую нагрузку. Школьники, как правило, стремятся их использовать в качестве средств стенографии, не понимая их прямого назначения, что совершенно недопустимо.

2) При использовании геометрической иллюстрации числовой прямой нет надобности соблюдать масштаб, указать направление и т.д. См. статью Г.В.Дорофеева в научно-методическом журнале "Математика в школе”: «Оценка решений стандартных задач в старшей школе", МвШ, 1999 г., №№ 2-4.