Треугольники

По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5,  но AH:AB – это косинус угла A, то есть $$\cos\angle A=\frac{4}{5}.$$ Рассмотрим прямоугольный треугольник AHB, в котором условно катет AH=4, а гипотенуза AB=5. По теореме Пифагора находим

$$BH=\sqrt{25-16}=3$$.

Тогда синус угла A равен $$\sin\angle A=\frac{3}{5}.$$ По следствию теоремы синусов имеем:

$$\frac{BC}{\sin A}=2R,$$

где R – радиус описанной окружности. Следовательно,

$$R=\frac{BC}{2\sin A}=\frac{12}{2\cdot0,6}=10.$$

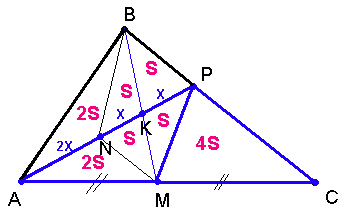
$$S_{∆KPCM}=5S$$

$$S_{∆ABC}=12S$$

$$\frac{S_{∆ABC}}{S_{∆KPCM}}=\frac{12S}{5S}=\frac{12}{5}=2,4$$

Пусть O - центр данной окружности, а Q - центр окружности, вписанной в треугольник ABC.

Точка касания M окружностей делит AC пополам.

Лучи AQ и AO - биссектрисы смежных углов, значит, угол OAQ прямой.

Из прямоугольного треугольника OAQ получаем:

$$AM^2=MQ\cdot MO$$

Тогда $$QM=\frac{AM^2}{OM}=\frac{9}{2}=4,5$$

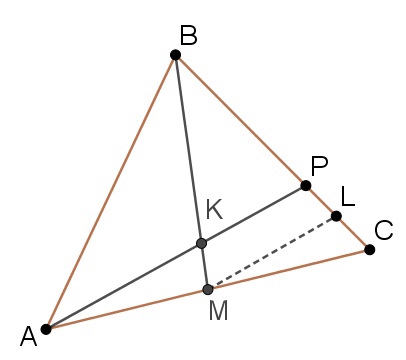
1) Пусть $$S_{ABC}=S$$. Тогда $$S_{ABM}=S_{BMC}=\frac{S}{2}$$.

2) Пусть $$ML||KP$$. По теореме Фалеса: $$\frac{AM}{MC}=\frac{PL}{LC}=\frac{1}{1}$$; $$\frac{BK}{KM}=\frac{BP}{PL}=\frac{4}{1}$$.

Тогда $$\frac{BP}{BC}=\frac{4}{6}=\frac{2}{3}$$.

3) $$\frac{S_{BKP}}{S_{BMC}}=\frac{BK\cdot BP}{BM\cdot BC}=\frac{4\cdot2}{5\cdot3}=\frac{8}{15}\Rightarrow S_{BKP}=\frac{8}{15}\cdot\frac{S}{2}=\frac{4}{15}S\Rightarrow\frac{S_{BKP}}{S_{ABC}}=\frac{4}{15}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!