ОГЭ
Задание 5560
В остроугольном треугольнике ABC угол B равен 60° . Докажите, что точки A, C, центр описанной окружности треугольника ABC и центр вписанной окружности треугольника ABC лежат на одной окружности.
1) $$O$$ - центр описанной окружности $$\Rightarrow$$ $$\angle AOC=2\angle ABC=120^{\circ}$$ (вписанный и центральный углы)
2) $$\angle A+\angle C=180^{\circ}-\angle B=120^{\circ}$$; $$\angle IAC=\frac{\angle A}{2}$$; $$\angle ICA=\frac{\angle C}{2}$$ ($$I$$ - центр вписанной $$\Rightarrow$$ $$AI$$ и $$CI$$ - биссектрисы) $$\Rightarrow$$ $$\angle IAC+\angle ICA=\frac{\angle A+\angle C}{2}=60^{\circ}$$ $$\Rightarrow$$ $$\angle AIC=120^{\circ}$$
3) из п.1 и п.2: $$\angle AOC=\angle AIC$$ (они опираются на одну сторону $$AC$$) $$\Rightarrow$$ $$AOIC$$ - вписанный четырехугольник.
Задание 6072
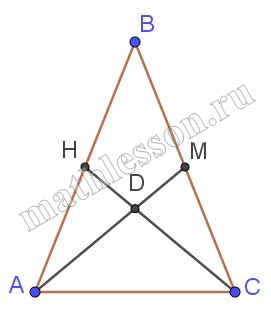
Докажите, что если у треугольника равны две медианы, то этот треугольник равнобедренный.
1) Пусть АМ=СН-медианы . $$\frac{LN}{LM}=\frac{2}{1}$$ и $$\frac{CL}{CH}=\frac{2}{1}$$(свойство медиан), но т.к. AM=CH, то AL=LC ,LH=LM.
2) $$\angle HLA=\angle MLC$$ (вертикальные) $$\Delta HLA=\Delta MLC$$ (по 2-м сторонам и углу между ними) $$\Rightarrow$$ AH=MC, но AH=HB и CM=MB $$\Rightarrow$$ AB=BC.
Задание 6166
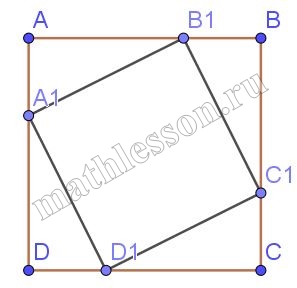
В квадрат, площадью 24 см2 вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон прямоугольника относятся как 1:3. Найдите площадь прямоугольника.
1) Пусть $$\angle B_{1}C_{1}B=\alpha$$ , тогда $$\angle D_{1}C_{1}C=90-\alpha$$ , тогда $$\angle C_{1}D_{1}C=\alpha$$ .
Рассуждая аналогично получим :
$$\angle B_{1}C_{1}B=\angle C_{1}D_{1}C =\angle DA_{1}D_{1}=\angle A_{1}B_{1}A=\alpha$$ , следовательно , $$\angle B_{1}C_{1}B\sim \angle C_{1}D_{1}C \sim \angle DA_{1}D_{1}\sim \angle A_{1}B_{1}A$$
2)т.к. $$B_{1}C_{1}:C_{1}D_{1}=1:3$$,то пусть $$B_{1}B=x\Rightarrow CC_{1}=3x, BC_{1}=y$$, тогда $$CD_{1}=3y.$$
3) т.к. $$A_{1}B_{1}=C_{1}D_{1}$$ и $$B_{1}C_{1}=A_{1}D_{1}$$ и все треугольники подобны , то $$\Delta A_{1}B_{1}A=\Delta C_{1}D_{1}C$$ и $$\Delta B_{1}C_{1}B=\Delta DA_{1}D_{1}$$ следовательно $$DD_{1}=x$$
4) из п. 3 получили, что $$BC=y+3x$$ и $$CD=x+3y$$, тогда
$$y+3x=x+3y\Rightarrow x=y$$
5)$$AC=\sqrt{S_{ABCD}}=\sqrt{24}$$
$$\frac{BC_{1}}{CC_{1}}=\frac{1}{3}\Rightarrow$$$$ BC_{1}=\frac{\sqrt{24}}{4}\Rightarrow$$$$CC_{1}=\frac{3\sqrt{24}}{4}$$
6) $$\Delta B_{1}BC_{1}$$: $$B_{1}C_{1}=\sqrt{(\frac{\sqrt{24}}{4})^{2}+(\frac{\sqrt{24}}{4})^{2}}=\sqrt{3}.$$Тогда $$C_{1}D_{1}=3\sqrt{3}.$$
7)$$S_{A_{1}B_{1}C_{1}D_{1}}=3\sqrt{3}*\sqrt{3}=9$$