ОГЭ
Задание 15291
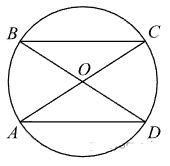
Вписанные углы ADB, CBD, ACB и DAC опираются на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен $$\frac{AO}{OC}$$
Поскольку AO = OC, эти треугольники равны, следовательно, AO = OC.
Задание 15578
Окружности с центрами в точках $$P$$ и $$Q$$ не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении $$m:n$$. Докажите, что диаметры этих окружностей относятся как $$m:n$$.
Задание 15993
Точка I равноудалена от точек A и B, поэтому эта точка лежит на серединном перпендикуляре к отрезку AB. Аналогично, точка J лежит на серединном перпендикуляре к отрезку AB. Значит, прямая, содержащая точки I и J, является серединным перпендикуляром к отрезку AB. Следовательно, прямые IJ и АВ перпендикулярны.
Задание 17153
В трапеции $$MNPK$$ с основаниями $$NP$$ и $$MK$$ диагонали пересекаются в точке $$F$$. Докажите, что площади треугольников $$MNF$$ и $$PKF$$ равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17257
Окружности с центрами в точках $$I$$ и $$J$$ пересекаются в точках $$A$$ и $$B$$, причём точки $$I$$ и $$J$$ лежат по одну сторону от прямой $$AB$$. Докажите, что прямые $$AB$$ и $$IJ$$ перпендикулярны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!