Системы с параметром

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

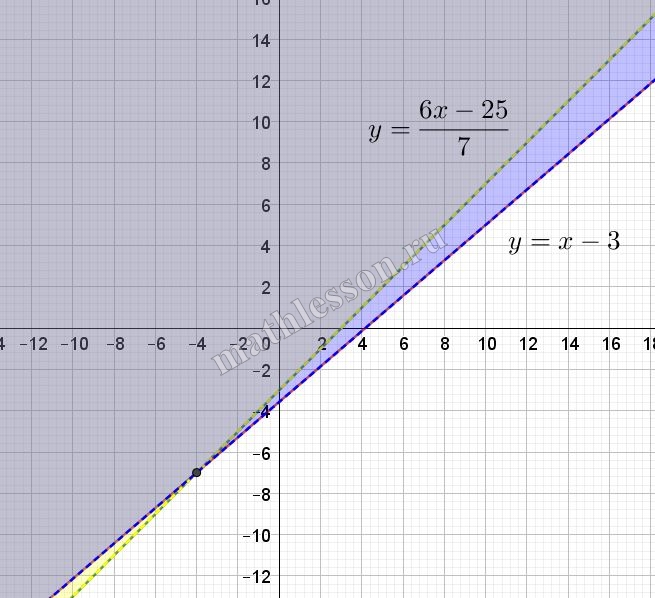
     Рассмотрим область определения данной системы. Так как даны логарифмы, то: $$\left\{\begin{matrix}3-x+y>0\\25-6x+7y>0\end{matrix}\right.\Rightarrow$$ $$\left\{\begin{matrix}y>x-3\\y>\frac{6x-25}{7}\end{matrix}\right.$$ (желтым выделено решение для первого неравенства, синим - для второго, серым - их пересечение)

     Рассмотрим первое уравнение системы:

$$\log_{2}(8(3-x+y))=\log_{2}(25-6x+7y)\Leftrightarrow$$$$24-8x+8y=25-6x+7y\Leftrightarrow$$$$y=2x+1 (1)$$

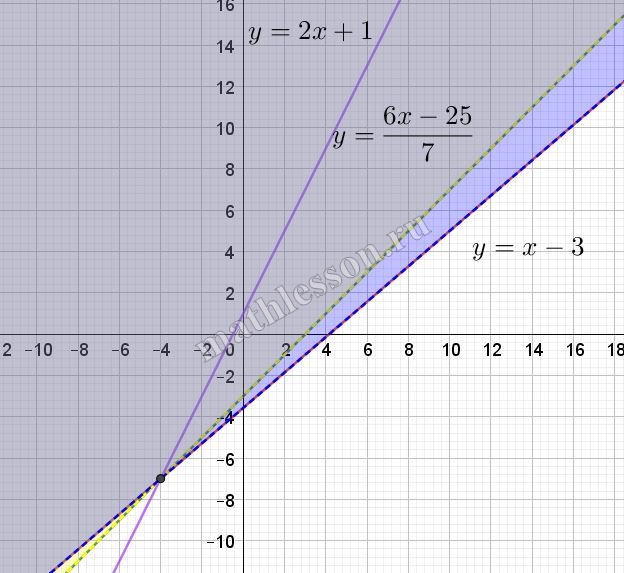
     Построим график данной функции с учетом области определения:

     Как видим, чтобы было два пересечения, x должен быть больше 4 (иначе часть прямой лежит вне области определения)

     Подставим  (1) во второе:$$2+2x+1=(x-2a)^{2}+a+2x\Leftrightarrow$$$$(x-2a)^{2}=3-a$$

     Так как число в квадрате, то правая часть уравнения должна быть больше нуля (если равна нулю, то корень всего один): $$3-a>0\Rightarrow a<3$$

     Рассмотрим график второй функции:

$$y+2=x^{2}-4ax+2a^{2}+a+2x\Leftrightarrow$$$$y=x^{2}+x(2-4a)+4a^{2}+a-2$$

     Найдем вершину параболы:

$$x_{0}=-\frac{2(1-2a)}{2}=2a-1$$

$$y_{0}=4a^{2}-4a+1-2(2a-1)^{2}+4a^{2}+a-2=8a^{2}-3a-1-8a^{2}+8a-2=5a-3$$

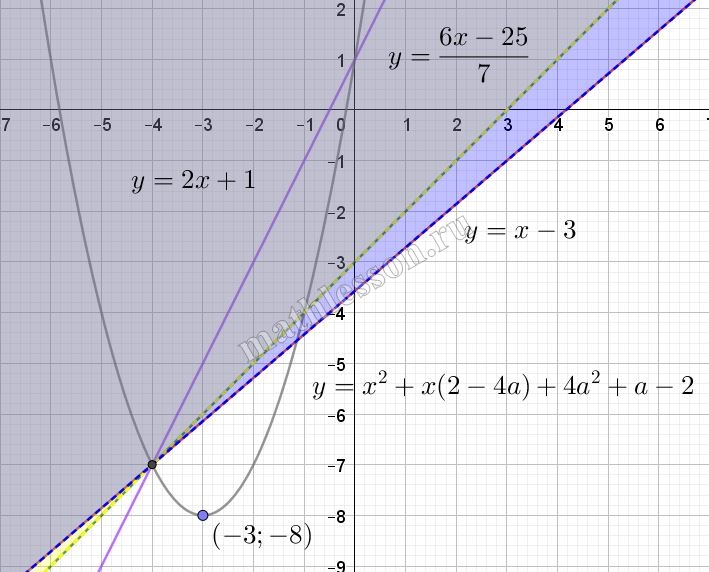
     Рассмотрим возможное расположение графика с учетом области определения:

     Как видим, координата y вершины параболы должна быть больше -8, а х больше -3 (если будет левее, то отно пересечение точно не попадет в область определения) :

$$\left\{\begin{matrix}2a-1>-3\\5a-3>-8\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a>-1\\a>-1\end{matrix}\right.$$

     С учетом того, что $$a<3$$, получаем: $$a \in (-1;3)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}\left | x \right |+2\left | y \right |+\left | 2y-3x \right | =12=f\\x^{2}+y^{2}=a=g\end{matrix}\right.$$

g - окружность с центром в начале координат и радиуса $$\sqrt{a}\Rightarrow a>0$$

     Рассмотрим график f:

При $$2y-3x\geq 0\Leftrightarrow$$ $$y\geq 1,5 x$$ получили $$\left | x \right |+2\left | y \right |+ 2y-3x =12$$

     В данном случае будет 3 части плоскости:

1)$$\left\{\begin{matrix}x\geq 0\\y\geq 0\end{matrix}\right.\Rightarrow$$ $$x+2y+2y-3x=12\Leftrightarrow$$ $$y=3+0,5x$$

2)$$\left\{\begin{matrix}x<0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$-x+2y+2y-3x=12\Leftrightarrow$$ $$y=3+x$$

3)$$\left\{\begin{matrix}x<0\\y<0\end{matrix}\right.\Leftrightarrow -x-2y+2y-3x=12\Rightarrow x=-3$$

     При $$2y-3x<0\Leftrightarrow y<1,5x$$ получим так же 3 части плоскости:

1)$$\left\{\begin{matrix}x\geq 0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$x+y-2y+3x=12\Leftrightarrow x=3$$

2)$$\left\{\begin{matrix}x\geq 0\\y<0\end{matrix}\right.\Leftrightarrow$$ $$x-y-2y+3x=12\Leftrightarrow y=-3+x$$

3)$$\left\{\begin{matrix}x<0\\y<0\end{matrix}\right.\Leftrightarrow$$ $$-x-y-2y+3x=12\Leftrightarrow y=x-3$$

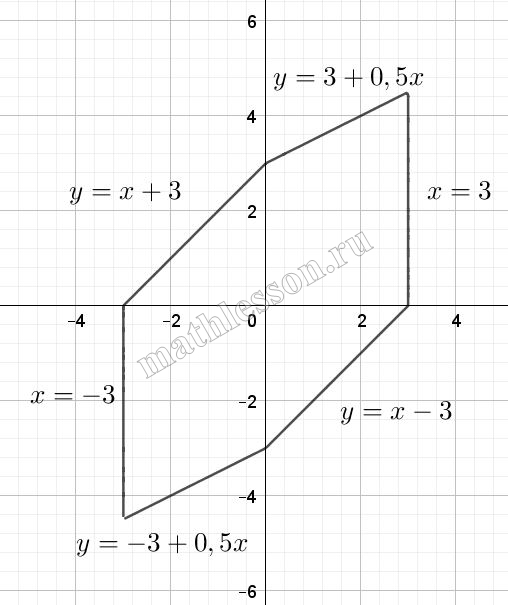
     Построим график данной функции .

     Очевидно , что 2 точки будет если пройдет через (C) и если касается в (B)

     Найдем координаты (C) :$$y=3+0,5=4,5$$.

Тогда $$OC=r_{1}^{2}=a=3^{2}+4,5^{2}=29,25$$. Найдем $$OB=r_{2}^{2}=a=1,5^{2}+1,5^{2}=4,5.$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}y(ax-1)=2\left | x+1 \right |+2xy\\xy+1=x-y\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y(ax-1-2x)=2\left | x+1 \right |\\y(x+1)=x-1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y=\frac{2\left | x+1 \right |}{ax-1-2x}\\y=\frac{x-1}{x+1}\end{matrix}\right.$$

Приравняем правые части функций: $$\frac{2\left | x+1 \right |}{ax-1-2x}=\frac{x-1}{x+1}$$. Раскрываем модуль:

     1) $$x+1\geq 0\Leftrightarrow x\geq -1\Leftrightarrow$$$$2(x+1)^{2}=(ax-1-2x)(x-1)\Leftrightarrow$$$$2x^{2}+4x+2=ax^{2}-ax-x+1-2x^{2}+2x\Leftrightarrow$$$$x^{2}(a-4)+x(-a-3)-1=0$$. Чтобы были корни, дискриминант должен быть неотрицательным: $$D=a^{2}+6a+9+4a-16=a^{2}+10a-7\geq 0$$. Так же корень из дискриминанта должен находится: $$D_{1}=100+28=128$$. Получаем: $$a_{1,2}=\frac{-10\pm \sqrt{128}}{2}=-5\pm 4\sqrt{2}$$

$$a \in (-\infty ; -5-4\sqrt{2}]\cup [-5+4\sqrt{2};+\infty )(*)$$ - условие возможного существованиях корней.

      При этом имеем параболу $$f(x)=x^{2}(a-4)+x(-a-3)-1$$. Рассмотрим случай, когда ни один корень не попадает в $$x\geq -1$$ (противоположный необходимому нам. То есть, найдя решения для данного случая, нам необходимо будет взять оставшийся промежуток. Например: пусть решением получим$$(0;1)$$, тогда для нахождения решений, чтобы хотя бы один корень попадал в промежуток от -1, мы возьмем $$(-\infty;0]\cup[1;+\infty)$$. Тогда абцисса вершины должна быть меньше -1, т.е. $$\frac{a+3}{2(a-4)}<-1$$ и если ветви вверх, то $$f(-1)>0$$ ветви вниз , то $$f(-1)<0$$

     Обоснование:

     Как видим, если ветви направлены вверх и f(-1)<0, то будет точно один корень, который попадет в промежуток от -1 до плюс бесконечности ($$x_{2}$$)

     Как видим, если ветви направлены вниз и f(-1)>0, то будет точно один корень, который попадет в промежуток от -1 до плюс бесконечности ($$x_{2}$$)

     Т.е. $$\left\{\begin{matrix} a-4>0\\ (a-4)+a+3-1>0\end{matrix}\right.$$ и $$\left\{\begin{matrix}a-4<0 & & \\(a-4)+a+3-1<0& &\end{matrix}\right.$$ или $$(a-4)(2a-2)>0$$

     Получаем : $$\left\{\begin{matrix}\frac{a+3}{2(a+4)}<-1\\(a-4)(a-1)>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{a+3+2a-8}{a-4}<0\\(a-4)(a-1)>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{3a-5}{a-4}<0\\(a-4)(a-1)>0\end{matrix}\right.$$

     Пересечений нет, значит случай невозможен и хотя бы один корень $$\geq -1$$. Тогда с учетом (*): $$a\in (-\infty ; -5-4\sqrt{2}]\cup [-5+4\sqrt{2}; +\infty )$$

     2) $$x+1<0\Rightarrow x<-1$$. Аналогично п.1

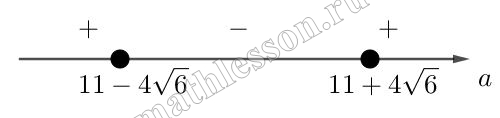
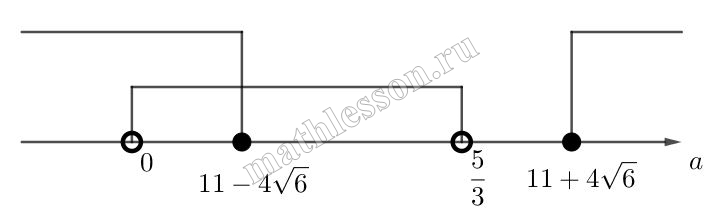
$$-2(x+1)^{2}=(ax-1-2x)(x-1)\Leftrightarrow$$$$-2x^{2}-4x-2=ax^{2}-ax-x+1-2x^{2}+2x\Leftrightarrow$$$$ax^{2}+x(-a+5)+3=0\Leftrightarrow$$$$D=a^{2}-100+25-12a=a^{2}-22a+25\geq 0\Leftrightarrow$$$$D=484-100=384\Leftrightarrow$$$$a_{1,2}=\frac{22\pm \sqrt{384}}{2}=11\pm 4\sqrt{6}\Leftrightarrow$$$$a \in (-\infty ; 11-4\sqrt{6}]\cup [11+4\sqrt{6};+\infty )$$

     Имеем параболу: $$f(x)=ax^{2}+x(5-a)+3$$

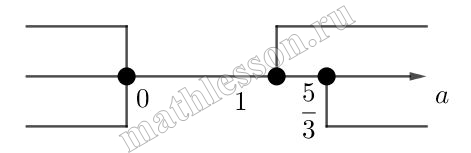
     Пусть оба корня $$>-1$$, тогда $$x_{0}\geq -1$$. И при ветвях вверх $$f(-1)\geq 0$$, при ветвях вних $$f(-1)\leq 0$$, т.е. $$\left\{\begin{matrix}a> 0\\a-5+a+3\geq 0\end{matrix}\right.$$ и $$\left\{\begin{matrix}a <0\\a-5+a+3\leq 0\end{matrix}\right.$$.Или $$a(2a-2)\geq 0$$. Тогда: $$\left\{\begin{matrix}\frac{a-5}{2a}\geq -1\\a(a-1)\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{a-5+2a}{2a}\geq 0\\a(a-1)\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{3a-5}{2a}\geq 0\\a(a-1)\geq 0\end{matrix}\right.$$

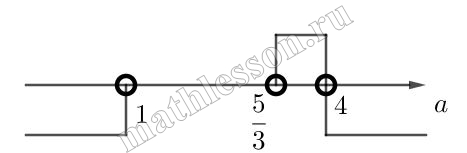
     Т.е. $$a \in (-\infty ; 0]\cup [\frac{5}{3};+\infty )(3)$$ с учетом $$a \in (-\infty ; 11-4\sqrt{6}]\cup [11+4\sqrt{6};+\infty )$$ и то, что промежуток (3) нас не удовлетворяет (мы должны взять наоборот $$(0;\frac{5}{3})$$ имеем:

     т.е. $$a\in (0; 11-4\sqrt{6}]$$

Сравним $$4\sqrt{2}-5$$ и $$11-4\sqrt{6}$$:

$$(4\sqrt{2}-5)^{2}=32-40\sqrt{2}+25=57-40\sqrt{2}\approx 0,43$$

$$(11-4\sqrt{6})^{2}=121-88\sqrt{6}+96=217-88\sqrt{6}\approx 1,44$$

     Объединим с (*) , тогда

     т.е. $$a \in (-\infty ;-5-4\sqrt{2}]\cup (0; +\infty )$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}(3\sqrt{x\left | x \right |}+\left | y \right |-3)(\left | x \right |+3\left | y \right |-9)=0(1)\\(x-a)^{2}+y^{2}=25(2)\end{matrix}\right.$$

     Рассмотрим (1) . Это совокупность графиков : $$3\sqrt{x\left | x \right |}+\left | y \right |-3=0$$ и $$\left | x \right |+3\left | y \right |-9=0$$

Т.к $$x\left | x \right |\geq 0$$, то $$x\geq 0$$, следовательно , получим $$3x+\left | y \right |-3=0$$ и $$x+3\left | y \right |-9=0$$ или $$\left\{\begin{matrix}\left[\begin{matrix}x=\frac{3-\left | y \right |}{3}\\x=9-3\left | y \right |\end{matrix}\right.(1)\\x\geq 0\end{matrix}\right.$$

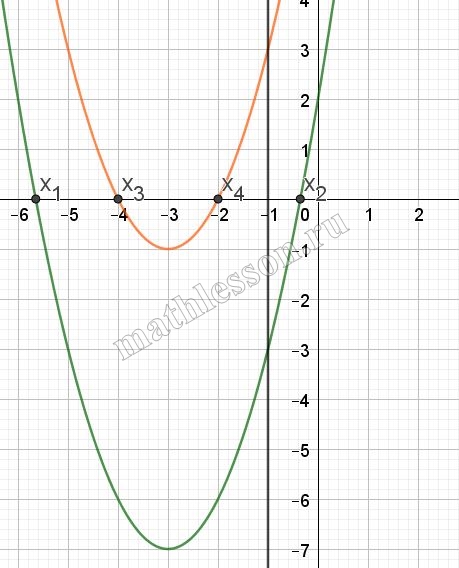
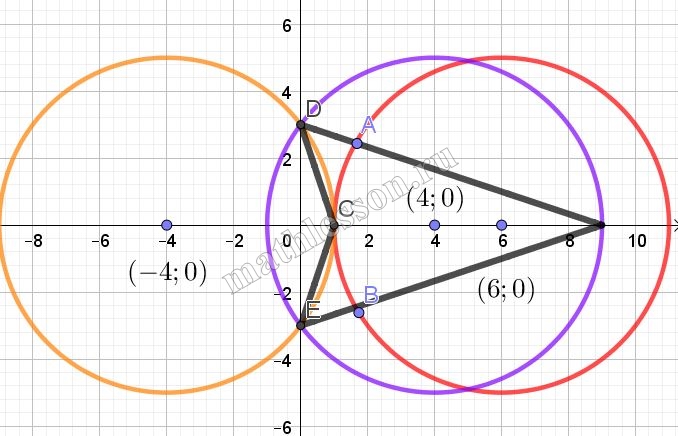
     (2): окружность радиуса 5 и центром (a;0). Построим график (1)

Тогда есть 3 случая, чтобы было 3 решения.

   1) Проходит через С (1;1) и центр правее этой точки (А;B)$$\Rightarrow a=6$$ (красная окружность) 

   2) Проходит через (1;1) и центр левее (D,C,E- точки пересечения)$$\Rightarrow a=-4$$ (оранжевая)

   3) Проходит через(0;3) ;(0;-3);(9;0) $$\Rightarrow a=4$$ (синяя)

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть m=y-a; n=x-a, тогда имеем

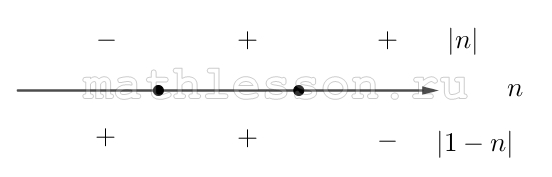
$$\left | m \right |+\left | 1-m \right |=2-\left | n \right |-\left | 1-n \right |(m(n))$$

Рассмотрим раскрытие модулей:

     1) $$n\leq 0$$: $$2-\left | n \right |-\left | 1-n \right |=1+2n$$. Тогда $$m(n)$$: $$\left | m \right |+\left | 1-m \right |=1+2n$$. Раскроем модули:

  a) $$m\leq 0$$: $$-2m+1=1+2n\Leftrightarrow$$ $$m=-n$$, с учетом, что $$n\leq 0$$ , то $$m=-n$$ при $$n=0$$ и $$m=0$$

  b) $$m \in (0;1]$$: $$1=1+2n\Leftrightarrow$$ $$n=0$$

  c) $$m \in (1;+\infty )$$: $$2m-1=1+2n\Leftrightarrow$$ $$m=n+1$$ при $$n\leq 0$$ – решений нет

     2) $$0<n\leq 1$$:$$ 2-\left | n \right |-\left | 1-n \right |=1$$

   a) $$m\leq 0$$: $$-2m+1=1\Leftrightarrow$$ $$m=0$$

   b) $$0<m\leq 1$$: $$1=1\Rightarrow$$ решение все точки в квадрате

$$\left\{\begin{matrix}0<n\leq 1\\0<m\leq 1\end{matrix}\right.$$

   c) $$m>0$$: $$2m-1=1\Rightarrow$$ $$m=1$$ решений нет

     3) $$n>1$$: $$2-\left | m \right |-\left | 1-n \right |=3-2n$$

   a) $$m\leq 0$$: $$-2m+1=3-2n\Leftrightarrow$$ $$m=n-1$$, с учетом , что $$n>1$$ решений нет

   b) $$a<m\leq 1$$: $$1=3-2n\Rightarrow$$ $$n=1\Rightarrow$$ решений нет

   c) $$m>1$$: $$2m-1=3-2n\Leftrightarrow$$ $$m=2-n$$ решений нет

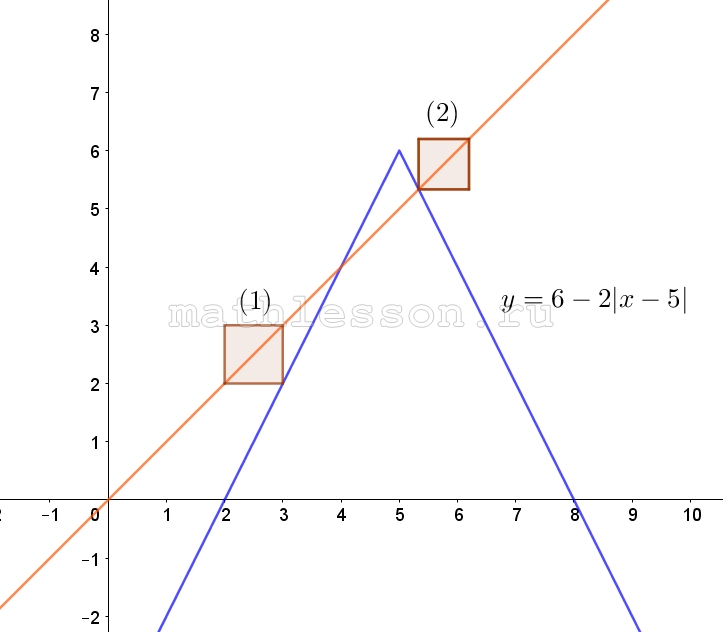
Построим график m(n). С учетом , что m=y-a и n=y-a , то график y(x) будет строиться смещение вершины (0;0) на (a;a) ( по прямой (y=x)), и построим график $$y=6-2\left | x-5 \right |$$ - cуществует 2 случая с одним решением :

1) При a=2

2) При пересечении вершиной и диагональю y=x части графика $$y=6-2\left | x-5 \right |$$(она задается y=16-2x)

$$\left\{\begin{matrix}y=x\\y=16-2x\end{matrix}\right.\Leftrightarrow$$ $$x=16-2x\Leftrightarrow$$ $$3x=16\Rightarrow$$ $$x=\frac{16}{3}\Rightarrow$$ $$a=\frac{16}{3}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

   Рассмотрим 2 уровнение системы . Т.к. $$\cos^{2}3x=1-\sin ^{2}3x$$ , и пусть $$\sin 3x=t$$ , тогда:

$$(\pi ^{2}(1-t^{2})-2 \pi ^{2}-72) y^{2}=2 \pi ^{2}(1+y^{2})t\Leftrightarrow$$$$(\pi ^{2}-\pi ^{2}t^{2}-2 \pi ^{2}-72-2 \pi ^{2}t ) y^{2}=2 \pi ^{2}t\Leftrightarrow$$$$(-\pi ^{2}(t^{2}+2t+1)-72)y^{2}=2 \pi ^{2}t\Leftrightarrow$$$$y^{2}=-\frac{2 \pi^{2} t}{(\pi ^{2}(t+1)^{2}+72)}\Rightarrow$$$$t\leq 0\Rightarrow$$ $$t \in [-1; 0]$$

   Рассмотрим $$f(t) =-\frac{2 \pi^{2} t}{(\pi ^{2}(t+1)^{2}+72)}$$; $$t \in [-1; 0]$$: $${f}' (t)=-2 \pi ^{2}(\frac{\pi^{2}(t+1)^{2}+72-t(2 \pi ^{2}(t+1))}{(\pi ^{2}(t+1)^{2}+72)^{2}}=$$$$\frac{-2 \pi ^{2}}{(\pi ^{2}(t+1)^{2}+72)^{2}}*(\pi ^{2}+72-\pi ^{2}t^{2})$$

   На промежутке $$t \in [-1; 0]$$, $${f}'(t) <0$$ $$\Rightarrow f(t)$$-убывает $$\Rightarrow$$ область значения $$E (f)\in [f(0); f(-1)]$$; $$f(0)=0; f(-1)=\frac{2 \pi ^{2}}{72}=\frac{\pi ^{2}}{36}$$; $$y^{2}\leq \frac{\pi ^{2}}{36}\Rightarrow$$ $$y \in [-\frac{\pi}{6}; \frac{\pi}{6}]$$

   Рассмотрим первое уравнение системы:

$$4 \sin ^{2}y-a=16 \sin ^{2}\frac{2x}{7}+9 ctg ^{2}\frac{2x}{7}\Leftrightarrow$$ $$a=4 \sin ^{2}y-(16 \sin ^{2}\frac{2x}{7}+9 (\frac{1 }{\sin ^{2}\frac{2x}{7}}-1))\Leftrightarrow$$$$a=4 \sin ^{2}y-(16 \sin ^{2}\frac{2x}{7}+9 * \frac{1}{\sin ^{2}\frac{2x}{7}}-9)\Leftrightarrow$$ $$a=4 \sin ^{2}y-((4 \sin \frac{2x}{7})^{2}-24 +(\frac{3}{\sin \frac{2x}{7}})^{2}-9+24)\Leftrightarrow$$ $$a=4 \sin ^{2}y-\frac{(4 \sin ^{2}\frac{2x}{7}-3)}{\sin ^{2}\frac{2x}{7}}-15$$

Так как $$a\rightarrow max$$, $$\sin ^{2}\frac{2x}{7}=\frac{3}{4}$$. Тогда: $$\sin \frac{2x}{7}=\pm \frac{\sqrt{3}}{2}\Leftrightarrow$$ $$\frac{2x}{7}=\pm \frac{\pi}{3}+\pi n , n \in Z\Leftrightarrow$$ $$x=\pm \frac{7 \pi }{6}+\frac{7 \pi n }{2}, n \in Z$$

Т.к. $$\sin 3x=-1\Rightarrow$$ $$3x=-\frac{\pi}{2}+2 \pi k , k \in Z$$, $$x=-\frac{\pi}{6}+\frac{2 \pi k}{3}, k \in Z$$

   Найдем n и k : $$\pm \frac{7 \pi}{6}+\frac{7 \pi n }{2}=-\frac{\pi}{6}+\frac{2 \pi k}{3}|*6\Leftrightarrow$$ $$\pm 7 \pi +21 \pi n =-\pi +4 \pi k\Leftrightarrow$$ $$6 \pi =21 \pi n -4 \pi k \Leftrightarrow$$ $$21 n -4k=6\Rightarrow$$ $$n=2, k=9$$. Следовательно, существует такой x. Тогда: $$a=4*(\frac{1}{2})^{2}-15 =-14$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Рассмотрим $$f(x) =x^{3}-(a+3)x^{2}+3ax$$, тогда в первом неравенстве записано $$f(x) +2x-2a\geq 0\Rightarrow$$ $$f(x)\geq 2a-2x$$. Пусть $$2a-2x=g(x)$$ , тогда имеем $$\left\{\begin{matrix}f(x)\geq g(x)\\g(x)\leq 0\end{matrix}\right.$$ и оно должно иметь единственное решение . При этом g(x) – прямая, функция убывает. Рассмотрим $$f(x)$$:

     $$x^{3}-(a+3)x^{2}+3ax=$$$$x(x^{2}-(a+3)x+3a)=$$$$x(x^{2}-ax-3x+3a)=$$$$x(x(x-a)-3(x-a))=x(x-a)(x-3)$$

     Изобразим схематичное решение системы:

     Очевидно , чтобы выполнялось условие единственного решения при $$f(x) \leq 0$$ необходимо, чтобы $$g(x_{0})=0$$. Если $$g(x_{0})>0$$ - решений нет, если $$g(x_{0})<0$$ решением будет множество точек из $$[g_{0} ;x_{0}]$$. При этом $$f(x)=0$$ при $$x=0 ;3 ;a$$.

     Есть три варианта расположения а:

     1) $$a<0$$: тогда $$g(3)=0\Rightarrow$$ $$2a-2*3=0\Rightarrow$$ $$a=3$$ - не подходит

     2) $$0\leq a\leq 3$$ : $$g(3) =0\Rightarrow$$ $$a=3$$ - решение

     3) $$a>3 \Rightarrow$$ $$g(a)=0\Rightarrow$$ $$2a-2a=0$$ – верное числовое равенство $$\Rightarrow$$ $$a>3$$

     Тогда $$a \in [3; +\infty )$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Вычтем из первого второе: $$2x^{2}+x(13-4a-4a-13)+8a^{2}=0$$

$$2x^{2}-8ax+8a^{2}=0$$

$$x^{2}-4ax+4a^{2}=0$$

$$(x-2a)^{2}=0$$ $$\Rightarrow$$ $$x=2a$$

Подставим в первое: $$8a^{3}+28a^{2}+(13-4a)2a+4a^{2}-2a+8=0$$

$$8a^{3}+28a^{2}+26a-8a^{2}+4a^{2}-2a+8=0$$

$$8a^{3}+24a^{2}+24a+8=0$$

$$a^{3}+3a^{2}+3a+1=0$$

$$(a+1)^{3}=0$$ $$\Rightarrow$$ $$a=-1$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!