Уравнения с параметром

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Вынесем $$\sqrt[3]{x}:$$ $$\sqrt[3]{x}(\sqrt[3]{1+\frac{1}{x}+\frac{x^{2}}{2}}+\sqrt[3]{1-\frac{1}{x}-\frac{x^{2}}{2}})=\sqrt[3]{x}*\sqrt[3]{a}$$

     Следовательно, $$\sqrt[3]{x}=0\Leftrightarrow x=0$$ является корнем, значит надо еще три отличных от 0 корня.

     Введем замену : $$\frac{x^{2}}{2}+\frac{1}{x}=t$$. Тогда: $$\sqrt[3]{1+t}+\sqrt[3]{1-t}=\sqrt[3]{a}$$

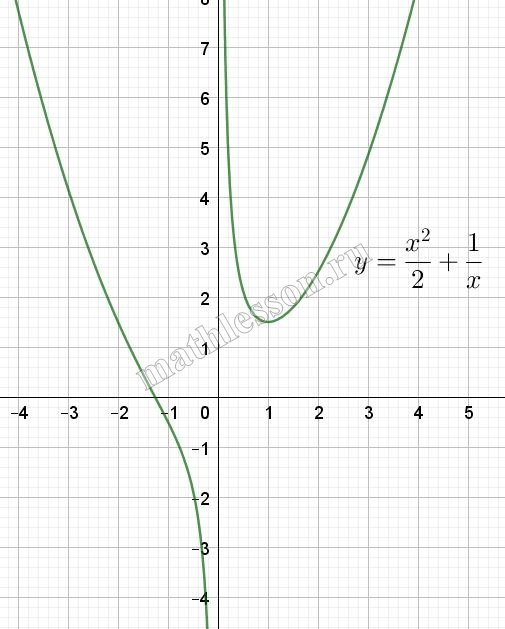
     Рассмотрим замену: пусть $$f(x)=\frac{x^{2}}{2}+\frac{1}{x}$$ и g(x)=t. g(x)=t – прямая, параллельная Ox. При этом f(x)-совмещенный график параболы и обратной пропорциональности. Исследуем график:

$$f(x)=0\Leftrightarrow$$ $$\frac{x^{2}+2}{2x}=0\Leftrightarrow$$ $$x=-\sqrt[3]{2}$$

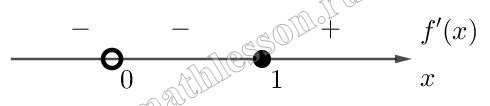
$$f'(x)=0\Leftrightarrow$$ $$x-\frac{1}{x^{2}}=0\Leftrightarrow$$ $$\frac{x^{3}-1}{x^{2}}=0$$

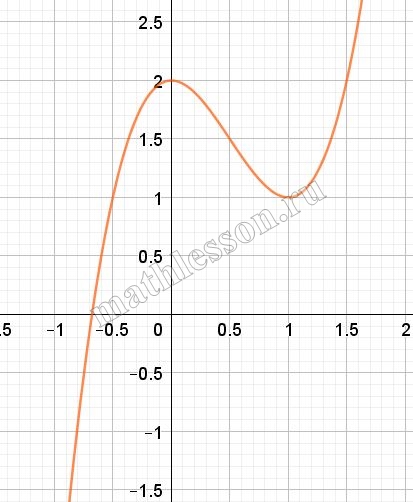
$$x=1$$  –точка минимума. При x=1: $$f(1)=\frac{1}{2}+1=1,5$$.

$$lim_{x\rightarrow -\infty} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$; $$lim_{x\rightarrow +\infty} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$

$$lim_{x\rightarrow -0} (\frac{x^{2}}{2}+\frac{1}{x})=-\infty$$; $$lim_{x\rightarrow +0} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$.

     При x=1: $$f(1)=\frac{1}{2}+1=1,5$$. Построим эскиз :

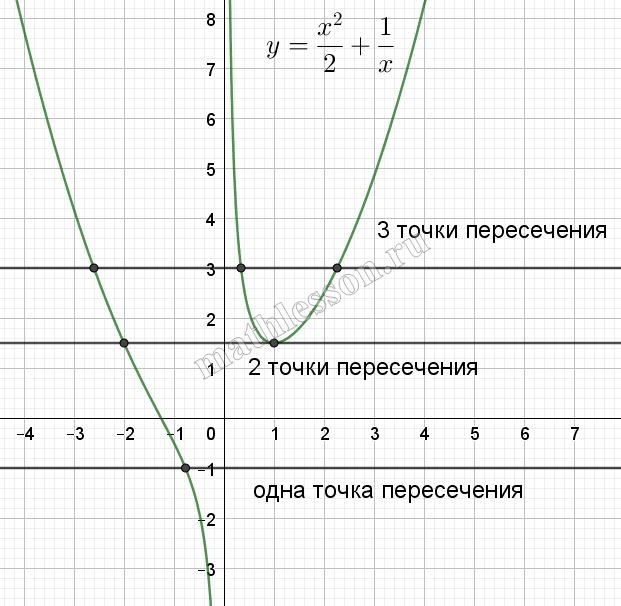
     Видим что при t<1,5-одно решение, при t=1,5-два решения , при t>1,5 – три решения.

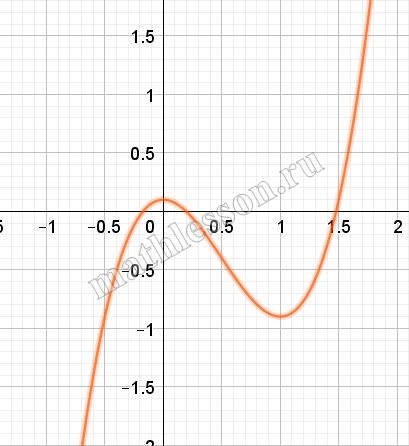
     Рассмотрим уравнение: $$\sqrt[3]{t+1}+\sqrt[3]{1-t}=\sqrt[3]{a}$$. Пусть $$f(t)=\sqrt[3]{1+t}+\sqrt[3]{1-t}; g(t)=\sqrt[3]{a}$$

     Построим график :

     Каждое пересечение при t<1,5 , дает одно решение, при t>1,5 даёт три решения и т.е. есть всегда 1(при t<0) , то нас не устраивает .

     При t=1,5 будет 2 решения, да еще одно ( область t<0)-следовательно, в общем получим 3, что и нужно .

     Найдем a : $$\sqrt[3]{1+\frac{3}{2}}+\sqrt[3]{1-\frac{3}{2}}=\sqrt[3]{a}$$

$$\sqrt[3]{\frac{5}{2}}-\sqrt[3]{\frac{1}{2}}=\sqrt[3]{a}\Leftrightarrow$$ $$\frac{\sqrt[3]{5}-1}{\sqrt[3]{2}} =\sqrt[3]{a}\Leftrightarrow$$ $$a=\frac{(\sqrt[3]{5}-1)^{3}}{2}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     $$3-2 \cos x=p(1+tg^{2}x)\Leftrightarrow$$ $$3-2\cos x=p*\frac{1}{\cos ^{2}x}$$

ОДЗ: $$\cos x\neq 0$$

     $$\frac{p}{\cos ^{2}x}+2 \cos x-3=0\Leftrightarrow$$ $$2 \cos ^{3}x-3 \cos ^{2}x+p=0$$

Замена: $$\cos x=t \in [-1;0)\cup (0;1]$$

$$2 t^{3}-3t^{2}+p=0$$

1 способ:

     Пусть $$f(t)=2t^{3}-3t^{2}+p$$

$${f}'(t)=6t^{2}-6t=0\Leftrightarrow$$ $$6t(t-1)=0\Rightarrow$$ $$t=0-max, t=1-min$$

     С учетом , что $$t \in [-1;0)\cup (0;1](1)$$ имеем следующие возможные расположения графика, при котором будет хотя бы одно решение из (1):

     1) $$\left\{\begin{matrix}f(-1)\geq 0\\f(0)>0\\f(1)\leq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2(-1)^{3}-3(-1)^{2}+p\geq 0\\p>0\\2(1)^{3}-3*1^{2}+p\leq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}p\geq 5\\p>0\\p\leq 1\end{matrix}\right.\Leftrightarrow$$ $$\varnothing$$

     2) $$\left\{\begin{matrix}f(-1)\leq 0\\f(0)>0\\f(1)\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}p\leq 5\\p>0\\p\geq 1\end{matrix}\right.\Leftrightarrow$$ $$p \in [1;5]$$

     3) $$\left\{\begin{matrix}f(-1)\leq 0\\f(0)>0\\f(1)\leq 1\end{matrix}\right. \Leftrightarrow$$ $$\left\{\begin{matrix}p\leq 5\\p>0\\p\leq 1\end{matrix}\right.\Leftrightarrow$$ $$p \in (0; 1]$$

     Итог: $$p \in (0;5]$$

2 способ:

     Рассмотрим график функции $$p=3t^{2}-2t^{3}$$. 

     Найдем экстремумы: $${f}'(t)=6t-6t^{2}=0\Leftrightarrow$$ $$6t(1-t)=0\Rightarrow$$ $$t=0-min, t=1-max$$

     Тогда $$p(0)=0; p(1)=1$$. При этом $$p(-1)=5$$. С учетом, что на промежутке от [-1;0) - убывает, а на (0;1] - возрастает, то $$p \in (0;5]$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     ОДЗ: $$\left\{\begin{matrix}a^{2}x^{3}-5a^{2}x^{2}+\sqrt{6-x} >0\\3-\sqrt{x-1}>0\\2+a^{2}>0\\x-1\geq 0\\6-x\geq 0\end{matrix}\right.$$

     Данная система будет иметь решения при следующих условиях: $$\left\{\begin{matrix}\left\{\begin{matrix}a^{2}x^{3}-5a^{2}x^{2}+\sqrt{6-x}=1\\3-\sqrt{x-1}=1\end{matrix}\right.(1)\\\left\{\begin{matrix}a^{2}x^{3}-5a^{2}x^{2}+\sqrt{6-x}= 3-\sqrt{x-1}\\2=2+a^{2}\end{matrix}\right.(2)\end{matrix}\right.$$

     Рассмотрим (1): $$3-\sqrt{x-1}=1\Leftrightarrow$$ $$2=\sqrt{x-1}\Leftrightarrow x=5$$. Тогда : $$a^{2}5^{3}-5a^{2}*5^{2}+\sqrt{6-5}=1\Leftrightarrow$$ $$1=1$$ - верное при $$\forall a\Rightarrow x=5$$ - решение (в ОДЗ попадает)

     Рассмотрим (2): $$2=2+a^{2}\Leftrightarrow$$ $$a^{2}=0\Leftrightarrow a=0$$, тогда нет смысла рассматривать , т.е. выполнение не при $$\forall a$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

       Если один из корней лежит на промежутке (0;1], то всегда будет ему симметричный относительно О на [-1;0)(например , $$\frac{1}{2}$$ и $$-\frac{1}{2}$$) т.к дано биквадратное уравнение . Чтобы было три корня существует 2 случая :

       1) $$x_{1}=x_{2}=0$$;$$x_{3,4}=\pm b_{m}$$; $$b_{m} \in (0;1)$$

       Если $$x_{1}=x_{2}=0$$, то $$a+\left | a \right |=0$$$$\Rightarrow$$ $$a<0$$. Получим : $$4a^{2}x^{4}+(2a-8)x^{2}+a-a=0\Leftrightarrow$$$$x^{2}(4a^{2} x^{2}+(2a-8))=0\Leftrightarrow$$ $$\left[\begin{matrix}x^{2}=\frac{8-2a}{4a^{2}}\\x^{2}=0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\pm \sqrt{\frac{8-2a}{4a^{2}}}\\x=0\end{matrix}\right.$$

       Учитывая, что $$\sqrt{\frac{8-2a}{4a^{2}}}<1$$ (если будет равен 1 , то ему симметричный =-1, не попадет в (-1; 1]):

       $$\left\{\begin{matrix}\frac{8-2a}{4a^{2}}<1\\\frac{8-2a}{4a^{2}}>0\\a<0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}4a^{2}+2a-8>0\\8-2a>0\\a<0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left[\begin{matrix}x<\frac{-1-\sqrt{33}}{4}\\x>\frac{-1+\sqrt{33}}{4}\end{matrix}\right.\\a<4\\a<0\end{matrix}\right.\Leftrightarrow$$ $$x<\frac{-1-\sqrt{33}}{4}$$

       2) Если один из корней равен 1, а симметричный $$\in (-1,1]$$(тогда $$-1 \in (-1;1]$$ и получим 3 корня):

       $$4a^{2}*1^{4}+(2a-8)*1^{2}+a+\left | a \right |=0\Leftrightarrow$$$$4a^{2}+2a-8+a+\left | a \right |=0$$

       Учитываем, что a>0 (смотреть п.1): $$4a^{2}+4a-8=0\Leftrightarrow$$ $$a^{2}+a-2=0\Leftrightarrow$$ $$\left[\begin{matrix}a=1\\a=-2(a<0)\end{matrix}\right.$$

       Сделаем проверку: при a=1: $$4x^{4}-6x^{2}+2=0$$$$\Leftrightarrow$$ $$2x^{4}-3x^{2}+1=0$$

       $$D=9-8=1$$ 

       $$x_{1,2}^{2}=\frac{3\pm 1}{4}=1, \frac{1}{2}$$$$\Rightarrow$$ $$x=\pm 1$$ и $$x=\pm \frac{\sqrt{2}}{2}$$ - три корня на (-1;1]

       Отдельно рассмотрим a=0

       $$4*0*x^{4}+(2*0-8)x^{2}+0+\left | 0 \right |=0\Leftrightarrow$$$$-8x^{2}=0\Rightarrow$$ $$x=0$$ - один корень

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

      $$(a-1)*4^{x}+(2a-3)*6^{x}=(3a-4)*9^{x}|:3^{2x}\Leftrightarrow$$$$(a-1)(\frac{2}{3})^{2x}+(2a-3)(\frac{2}{3})^{x}-(3a-4)=0$$

Пусть: $$(\frac{2}{3})^{x}=y>0$$

      $$(a-1) *y^{2}+(2a-3)y-(3a-4)=0$$

      $$D=(2a-3)^{2}+4(a-1)(3a-4)=16a^{2}-40a+25=(4a-5)^{2}$$

$$y_{1}=\frac{3-2a+\left | 4a-5 \right |}{2(a-1)}$$

$$y_{2}=\frac{3-2a-\left | 4a-5 \right |}{2(a-1)}$$

      Существуют следующие варианты единственного решения :

1) $$y_{1}=y_{2}\Rightarrow$$ $$4a-5=0\Rightarrow$$ $$a=\frac{5}{4}$$. Выполним проверку: $$(\frac{2}{3})^{x}=\frac{3-2,5}{2(1,25-1)}=1\Rightarrow$$ $$x=0$$ - один корень

2) Один из корней меньше или равен 0 , второй больше 0. Сравним корни: $$\frac{3-2a+\left | 4a-5 \right |}{2(a-1)}>\frac{3-2a-\left | 4a-5 \right |}{2(a-1)}$$$$\Leftrightarrow$$ $$\frac{2\left | 4a-5 \right |}{2(a-1)}>0$$$$\Leftrightarrow$$ $$\frac{\left | 4a-5 \right |}{a-1}>0$$$$\Rightarrow$$

При $$a>1: y_{1}>y_{2}$$;

При $$a<1 : y_{2}>y_{1}$$,

Тогда решение будет при условии: $$\left[\begin{matrix}\left\{\begin{matrix}a>1\\y_{2}\leq 0& &\end{matrix}\right.(1)\\\left\{\begin{matrix}a<1\\y_{1}\leq 0\end{matrix}\right. (2)\end{matrix}\right.$$

Рассмотрим системы отдельно:

(1):    $$\left\{\begin{matrix}a>1\\\frac{3-2a-\left | 4a-5 \right |}{a-1}\leq 0 & &\end{matrix}\right.$$$$\Leftrightarrow$$$$\left\{\begin{matrix}a>1\\\left | 4a-5 \right |\geq 3-2a\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a>1\\\left[\begin{matrix}4a-5\geq 3-2a\\4a-5\leq 2a-3\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a>1\\\left[\begin{matrix}a\geq \frac{4}{3}\\a\leq 1\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$a \in [\frac{4}{3}; +\infty )$$

(2):    $$\left\{\begin{matrix}a<1\\\frac{3-2a+\left | 4a-5 \right |}{2(a-1)} \leq 0\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a<1\\3-2a+\left | 4a-5 \right |\geq 0\end{matrix}\right.$$$$\Leftrightarrow$$$$\left\{\begin{matrix}a<1\\\left | 4a-5 \right |\geq 2a-3\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a<1\\\left[\begin{matrix}4a-5\geq 2a-3\\4a-5\leq 3-2a\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$$$\left\{\begin{matrix}a<1\\\left[\begin{matrix}a\geq 1\\a\leq \frac{4}{3}\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$a<1$$

      Проверим случай $$a=1$$: $$-6^{x}=-9^{x}\Rightarrow$$ $$x=0$$ - один корень

      Тогда конечный ответ: $$a \in (-\infty ;1]\cup {\frac{5}{4}}\cup [\frac{4}{5}; +\infty )$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

        Так как $$x<\frac{1}{3}$$, то $$\frac{1}{x}-2>1$$. Пусть $$\frac{1}{x}-2=y$$. Тогда получим : $$a \log_{y}4=\log_{2}y-b$$$$\Leftrightarrow$$ $$2a \log_{y}2+b=\log_{2}y$$

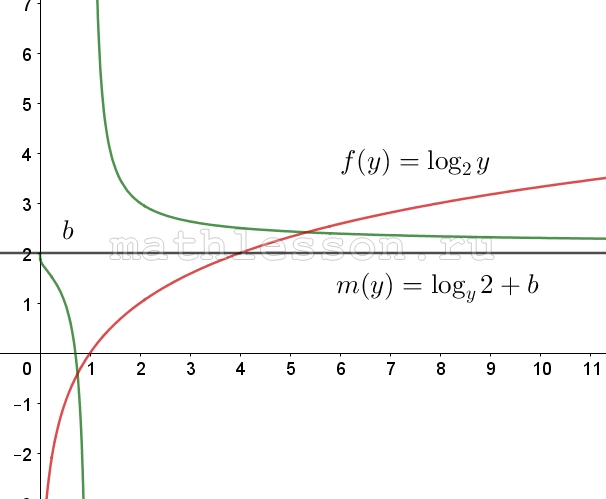
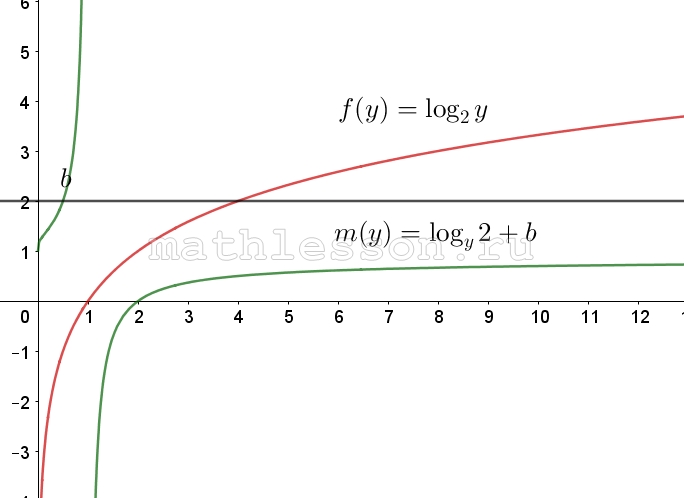
        Пусть $$f(y)=2a \log_{y}2+b$$ и $$g(y)=\log_{2}y$$

        Рассмотрим $$f(y)$$: данный график имеет растяжение по Oy и располагается так же как $$m(y)=\log_{y}2+b$$ при $$a>0$$. При a<0 симметрично отобразится относительно Ox .

        Необходимо решение при y>1. На данном промежутке $$m(y)=\log_{y}2+b$$ убывает, при этом $$\lim _{y\rightarrow \infty }m(y)=b$$ и предел достигается сверху. Следовательно, при a>0 и b>0, $$\lim _{y\rightarrow \infty }f(y)=b\Rightarrow$$ будет пересечение с g(y) , т.к. $$\lim_{y\rightarrow \infty }g(y)=\infty$$

        При $$a<0$$ , $$f(y)$$ на $$y>1$$ возрастает и $$\lim _{y\rightarrow \infty } f(y)=b$$. При этом предел достигается снизу, и так как в задании необходимо решение для любого положительного b, а, например, при b=0,1, пересечений графика f(y) и g(y) не будет. Следовательно, данный промежуток мы не учитываем.

        При a=0 имеем $$\log_{2}y=b\Rightarrow y=2^{b}$$. Т.к. $$b>0$$, то $$y>1$$ $$\Rightarrow$$ $$a \in [0;+\infty)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть $$(x)=\frac{x(3^{x}-1)}{3^{x}+1}$$ и $$g(x)=a^{2}+1$$

     1) $$f(x) \geq 0$$ при любом x. Найдем промежутки возрастания и убывания: $${f}'(x)=\frac{(x{(3^{x}-1)}'(3^{x}+1)-{(3^{x}+1)}'(x(3^{x}-1)))}{(3^{x}+1)^{2}}=0|* (3^{x}+1)^{2}\Leftrightarrow$$$$((3^{x}-1)+x*3^{x}\ln 3)(3^{x}+1)-3 ^{x}\ln 3* x(3^{x}-1)=0\Leftrightarrow$$ $$3 ^{2x}-1+3^{2x}*x\ln 3+x*3^{x}\ln 3-x*3^{2x}\ln 3 +3 ^{x}*x\ln 3=0\Leftrightarrow$$ $$3 ^{2x}-1+2x*3^{2x}\ln 3=0\Leftrightarrow$$ $$3^{2x}+2x*3 ^{x}\ln 3=1\Leftrightarrow$$ $$1-2x\ln3=3^{x}$$

     Пусть $$m(x)=1-2x\ln 3$$ и $$n(x) =3^{x}$$: m(x) - линейная убывающая и n (x)-степенная возрастающая $$\Rightarrow$$ одна точка пересечения x=0

     Для f(x): x=0 - точка минимума $$\Rightarrow$$ $$(-\infty ; 0)$$ – убывает монотонно, $$(0; +\infty )$$ - возрастает . При этом

$$\left | \frac{x(3^{x}-1)}{3^{x}+1}-2a \right |=f_{1}(x)$$ - это график f(x), у которого вся часть графика под Ox отражается симметрично относительно Ox. g(x) –прямая, параллельная Ox ($$a^{2}+1>0$$, при любом a ). Тогда возможен только один вариант нечетного числа корней, когда $$\left | 2a \right |=a^{1}+1\Leftrightarrow$$ $$a^{2}-\left | 2a \right |+1=0\Leftrightarrow$$ $$(\left | a \right |-1)^{2}=0\Leftrightarrow$$ $$a=\pm 1$$

     2) Возможно решение с использованием инвариантности: доказать четность левой функции (f(-x)=f(x)), тогда нечетное количество решений будет лишь в том случае, когда один из корней равен 1. Подставить вместо х в начальное уравнение 1 и получим сразу уравнение отностильно а

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

   ОДЗ: $$\left\{\begin{matrix}2-x>0\\2ax+3a^{2}\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x<2(1)\\2ax+3a^{2}\geq 0 (2)\end{matrix}\right.$$

   Решение: $$\lg(2-x)(\sqrt{2ax+3a^{2}}-x)=0\Leftrightarrow$$ $$\left\{\begin{matrix}\lg(2-x)=0\\\sqrt{2ax+3a^{2}}=x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2-x=1\\\left\{\begin{matrix}2ax+3a^{2}=x^{2}\\x\geq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=1\\\left\{\begin{matrix}\left\{\begin{matrix}x_{2}=3a\\x_{3}=-a\end{matrix}\right.\\x\geq 0\end{matrix}\right.\end{matrix}\right.$$

   Т.к. $$x\geq 0$$, то $$x_{2}$$ и $$x_{3}$$ будут одновременно существовать , если $$x_{2}=x_{3}=0\Rightarrow a=0$$, условие двух корней соблюдается. В противном случае решениями будут $$x_{1}$$ и $$x_{2 }$$ или $$x_{1}$$ и $$x_{3}$$. При этом , чтобы было два корня , должно выполняться ОДЗ:

$$\left\{\begin{matrix}\left\{\begin{matrix}x_{1}\in (2)\\x_{2} \in (1)\\x_{2}\geq 0\end{matrix}\right.\\\left\{\begin{matrix}x_{1}\in (2)\\x_{3}\in (1)\\x_{3}\geq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left\{\begin{matrix}2a*1+3a^{2}\geq 0\\0\leq 3a<2\end{matrix}\right.\\\left\{\begin{matrix}2a*1+3a^{2}\geq 0\\0\leq -a<2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left\{\begin{matrix}x \in (-\infty -\frac{2}{3}]\cup [0 +\infty )\\a \in [0 \frac{2}{3})\\\end{matrix}\right.\\\left\{\begin{matrix}a \in (-\infty -\frac{2}{3}]\cup [0 +\infty )\\-2<a\leq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$a \in (-2; -\frac{2}{3}]\cup [0; \frac{2}{3})$$

   $$x_{1}$$ и так входит в [0 ;2) , потому проверяется только условие (2) для него , $$x_{2}$$ и $$x_{3}$$ и так получились из (2) , потому проверим (1) для них. При этом учитываем, что $$x_{1}\neq x_{2}$$ и $$x_{1}\neq x_{3}$$, иначе получим 1 корень $$\Rightarrow$$ $$3a\neq 1\Rightarrow$$ $$a\neq \frac{1}{3}$$ и $$-a\neq 1\Rightarrow$$ $$a\neq -1$$. Тогда: $$a \in (-2; -1)\cup (-1 ;-\frac{2}{3}]\cup(0 ;\frac{1}{3})\cup [\frac{1}{3}; \frac{2}{3}]$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$(\cos x-1)^{2}=a(3 \cos x+4 \sin ^{2}x-8)\Leftrightarrow$$ $$(\cos x-1)^{2}=a(3 \cos x+4-4\cos^{2}x-8)\Leftrightarrow$$ $$(\cos x-1)^{2}=a(3\cos x-4 \cos ^{2}x-4)$$

     Рассмотрим правую часть : -$$4 \cos^{2}x-4 \in [-8 ;-4]$$ $$(\cos ^{2}x \in [0 ;1] )\Rightarrow$$ $$3 \cos x-4 \cos ^{2}x-4\leq -1$$ при любом x) , при этом $$(\cos x-1)^{2}\geq 0\Rightarrow$$ чтобы выполнялось решение должно быть $$a<0$$ (при a=0 получим, что $$\cos x-1=0 \Rightarrow$$ $$\cos x=1\Rightarrow$$ $$x=2 \pi n \notin (0 \frac{\pi}{2}]$$)

     При этом, чтобы было решение на $$(0 ;\frac{\pi}{2}]$$, то $$\cos x \in [0; 1)$$

     Сделаем замену $$\cos x=t \in [-1; 1]$$: $$(t-1)^{2}=a(3t-4t^{2}-4)\Leftrightarrow$$ $$\frac{(t-1)^{2}}{a}=-4t^{2}+3t-4$$

     Рассмотрим функции : $$f_{1}(t)=\frac{(t-1)^{2}}{a}$$ и $$f_{2}(t)=4t^{2}+3t-4p$$

• $$f_{2}(t): t_{0}=-\frac{3}{-8}=\frac{3}{8}\Rightarrow$$ $$f_{2}(t_{0})=-\frac{55}{16}$$ - парабола, ветви вниз, вершина $$(\frac{3}{8};-\frac{55}{16})$$, сужение к оси симметрии
• $$f_{1}(t)$$: парабола, вершина (1; 0) , ветви в зависимости от a ($$a<0 \Rightarrow$$ вниз )

     При этом необходимо единственное решение на $$x \in (0 ;\frac{\pi}{2}]\Rightarrow$$ $$\cos x \in [0; 1) \Rightarrow$$ $$t \in [0; 1)$$ -единственное решение на данном промежутке.

     Решение такое будет при $$f_{1}(0)\leq -4$$ $$\Rightarrow$$ $$\frac{(01)^{2}}{a}\leq -4\Rightarrow$$ $$\frac{1}{a}\leq -4\Leftrightarrow$$ $$\frac{1+4a}{a}\leq 0\Rightarrow$$ $$a\in [-\frac{1}{4};0)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Пусть $$f(x)=7\sqrt{2x^{2}+49}$$ и $$g(x)=2x+x|x-7a|-5|x|-a^{2}$$. Рассмотрим g(x): если $$7a>0$$, то получим следующее раскрытие модулей:

$$\left[\begin{matrix}\left\{\begin{matrix}x<0\\g(x)=5x+14a-a^{2}\end{matrix}\right.\\\left\{\begin{matrix}0\leq x\leq 7a\\g(x)=5x+14a-a^{2}\end{matrix}\right.\\\left\{\begin{matrix}x>7a\\g(x)=-x-14a-a^{2}\end{matrix}\right.\end{matrix}\right.$$

     Если же $$7a<0$$, то:

$$\left[\begin{matrix}\left\{\begin{matrix}x<7a\\g(x)=5x+14a-a^{2}\end{matrix}\right.\\\left\{\begin{matrix}7a\leq x\leq 0\\g(x)=9x-14a-a^{2}\end{matrix}\right.\\\left\{\begin{matrix}x>0\\g(x)=-x-14a-a^{2}\end{matrix}\right.\end{matrix}\right.$$

     В обоих случаях необходимо, чтобы $$g(0)\geq f(0)$$:

$$\left[\begin{matrix}\left\{\begin{matrix}a>0\\14a-a^{2}\geq 49\end{matrix}\right.\\\left\{\begin{matrix}a<0\\-14a-a^{2}\geq 49\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}\left\{\begin{matrix}a>0\\a^{2}-14a+49\leq 0\end{matrix}\right.\\\left\{\begin{matrix}a<0\\a^{2}+14a+49\leq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}\left\{\begin{matrix}a>0\\(a-7)^{2}\leq 0\end{matrix}\right.\\\left\{\begin{matrix}a<0\\(a+7)^{2}\leq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$a=\pm 7$$

     При $$a=0$$ получим: $$7\sqrt{2x^{2}+49}=2x+2|x|-5|x|\Leftrightarrow$$$$7\sqrt{2x^{2}+49}=2x-3|x|$$ - решений не имеет, так как левая часть всегда больше нуля, а правая - меньше.

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$a^{2}\ctg^{2}x-9a+a^{2}=4a\sin x$$

$$a(a\cdot\ctg^{2}x-9+a-4\sin x)=0$$

1) При $$a=0$$ корни есть

2) При $$a\neq0$$: $$a(ctg^{2}x+1)-9-4\sin x=0$$

$$a(\frac{\cos^{2}x}{\sin^{2}x}+1)-9-4\sin x=0$$

$$a\cdot(\frac{1}{\sin^{2}x})-9-4\sin x=0$$

Пусть $$\sin x=y$$

$$\left\{\begin{matrix}\frac{a}{y^{2}}-9-4y=0&\\y\neq0&\\y\in[-1;1]&\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{a}{y^{2}}=4y+9&\\y\neq0&\\-1\leq y\leq1&\end{matrix}\right.$$

Пусть $$f(y)=\frac{a}{y^{2}}$$; $$g(y)=4y+9$$

При $$f(1)\leq g(1)$$ получим наличие корней. При этом $$a$$ должно быть меньше $$0$$, иначе ветви $$f(y)$$ вниз и $$f(y)<0$$ при всех $$y$$. Т.к. $$f(y)$$ симметричен от оси ординат, то $$f(1)\leq g(1)$$ достаточно $$\frac{a}{1}\leq4\cdot1+9$$ $$\Rightarrow$$ $$a\leq13$$ $$\Rightarrow$$ $$a\in(0;13]$$. С учетом (1) получим $$a\in[0;13]$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!