ЕГЭ Профиль
Задание 6618
Точка N делит диагональ трапеции ABCD в отношении CN:NA=2:1. Длины оснований ВС и AD относятся как 1:3. Через точку N и вершину D проведена прямая, пересекающая боковую сторону АВ в точке М.
A) 1) Пусть $$BC=x\Rightarrow$$ $$AD=3x$$; $$CN=2y\Rightarrow$$ $$AN=y$$
2) $$\angle CAD=\angle BCA$$(накрест лежащие ). Пусть $$\angle CAD=\alpha$$
3) $$S_{BCA}=\frac{1}{2}BC*AC*\sin BCA=$$$$\frac{1}{2}*x*3y*\sin \alpha =\frac{3xy \sin \alpha }{2}$$
$$S_{CAD}=\frac{1}{2}*AC*AD \sin CAD=$$$$\frac{1}{2}*3y*3x\sin \alpha =\frac{9xy\sin \alpha }{2}$$
$$S_{ABCD}=S_{BCA}+S_{CAD}=$$$$6xy\sin \alpha =S$$, тогда: $$S_{CAD}=\frac{3}{4}S$$, $$S_{BCA}=\frac{1}{4}S$$
4) $$S_{BCN}=\frac{1}{2}BC*CN*\sin BCN=$$$$\frac{1}{2}*x*2y*\sin \alpha =$$$$xy\sin \alpha =\frac{1}{6}S\Rightarrow$$ $$S_{BNA}=\frac{1}{4}S-\frac{1}{6}S=\frac{1}{12}S$$
5) $$\Delta BNC\sim \Delta ANH$$ ($$BN\cap AD=H$$) $$\Rightarrow$$ $$\frac{CN}{AN}=\frac{BN}{NH}=\frac{2}{1}=$$$$\frac{BC}{AH}\Rightarrow$$ $$AH=\frac{BC}{2}=\frac{x}{2}\Rightarrow$$ $$HD=3x-\frac{x}{2}=\frac{5x}{2}$$
6) По т. Менелая для $$\Delta MDA$$:
$$\frac{BN}{NH}*\frac{HD}{AD}*\frac{AM}{MB}=1\Leftrightarrow$$ $$\frac{2}{1}*\frac{5x}{2*3x}*\frac{AM}{MB}=1\Rightarrow$$ $$\frac{AM}{MB}=\frac{3}{5}\Rightarrow \frac{MB}{AB}=\frac{5}{8}$$
7) $$S_{MBN}=\frac{MB}{AB}*S_{BNA}=$$$$\frac{5}{8}*\frac{1}{12}S=\frac{5S}{96}$$
8) $$S_{MBCN}=\frac{5S}{96}+\frac{S}{6}=$$$$\frac{5S+16S}{96}=\frac{21S}{96}=\frac{7S}{32}$$
Б) 1)По т. Менеая для $$\Delta ABH$$:
$$\frac{DN}{NM}*\frac{MB}{AB}*\frac{AH}{HD}=1\Leftrightarrow$$ $$\frac{DH}{NM}*\frac{5}{8}*\frac{1}{5}=1\Leftrightarrow$$ $$\frac{DN}{NM}=\frac{8}{1}\Rightarrow$$ $$MN=\frac{1}{9}*9=1$$
Задание 6827
В прямоугольном треугольнике АВС из точки Е, расположенной в середине катета ВС, опущен перпендикуляр EL на гипотенузу АВ. $$AE=\sqrt{10}EL$$, $$BC>AC$$

A) 1) пусть $$EL=x$$$$\Rightarrow$$ $$AE=x\sqrt{10}$$. Тогда из $$\Delta ELA:$$ $$AL=\sqrt{AE^{2}-EL^{2}}=3x$$
2) Пусть $$BL=y$$ $$\Rightarrow$$. Тогда из $$\Delta EBL:$$$$BE=\sqrt{BL^{2}+EL^{2}}=\sqrt{x^{2}+y^{2}}=EC$$
3) $$\Delta EBL\sim \Delta ABC$$ $$\Rightarrow$$ $$\frac{EB}{AB}=\frac{BL}{BC}$$$$\Leftrightarrow$$ $$\frac{\sqrt{x^{2}+y^{2}}}{y+3x}=\frac{y}{2\sqrt{x^{2}+y^{2}}}$$$$\Leftrightarrow$$ $$2(x^{2}+y^{2})=y^{2}+3xy$$$$\Leftrightarrow$$ $$2x^{2}+2y^{2}-y^{2}-3xy=0\Leftrightarrow$$ $$2x^{2}-3xy+y^{2}=0$$
$$D=9y^{2}-8y^{2}=y^{2}\Rightarrow$$ $$x=\frac{3y\pm y}{4}$$$$\Rightarrow$$ $$x=y$$ или $$x=\frac{y}{2}$$
- Если $$x=y$$ , то $$AB=4x$$ ; $$BC=2x\sqrt{2}$$$$\Rightarrow$$ $$AC=\sqrt{16x^{2}-8x^{2}}=2x\sqrt{2}$$ (но BC>AC)
- Если $$x=\frac{y}{2}$$$$\Rightarrow$$ $$AB=5x; BC=2x\sqrt{5}$$$$\Rightarrow$$ $$AC=\sqrt{25x^{2}-20x^{2}}=x\sqrt{5}$$
4) $$\angle C=90$$; $$\angle A=arcsin \frac{BC}{AB}=arcsin \frac{2\sqrt{5}}{5}$$; $$\angle B=arcsin \frac{AC}{AB}=arcsin \frac{\sqrt{5}}{5}$$
Б) 1) $$\cos \angle A=\sin B=\frac{\sqrt{5}}{5}\Rightarrow$$ из $$\Delta ALC:$$ $$CL=\sqrt{AC^{2}+AL^{2}-2 AC*AL*\cos A}=2\sqrt{2}x$$$$\Rightarrow$$ $$\frac{AE}{CL}=\frac{\sqrt{10}x}{2\sqrt{2}x}=\frac{\sqrt{5}}{2}$$
Задание 6878
Внутри параллелограмма ABCD взята точка К так, что треугольник CKD равносторонний. Известно, что расстояния от точки К до прямых AD, AB и ВС равны соответственно 3, 6 и 5.
A) Пусть $$CD=KD=KC=a$$, тогда из $$\Delta NKD$$ : $$ND=\sqrt{a^{2}-3^{2}}$$; Из $$\Delta KRC$$: $$RC=\sqrt{a^{2}-5^{2}}$$
2) Пусть $$DH\perp BC$$ , тогда $$DH=NR=8$$; $$CH=ND=RC=\sqrt{a^{2}-3^{2}}-\sqrt{a^{2}-5^{2}}$$. $$\Delta DHC$$: $$a^{2}=8^{2}+(\sqrt{a^{2}-3^{2}}-\sqrt{a^{2}-5^{2}})^{2}\Leftrightarrow$$$$a^{2}-8^{2}=2a^{2}-34-2\sqrt{a^{4}-34a^{2}+225}\Leftrightarrow$$$$2\sqrt{A^{4}-34a^{2}+225}=a^{2}+30\Leftrightarrow$$$$4a^{4}+136a^{2}+900=a^{4}+60a^{2}+900\Leftrightarrow$$$$3a^{4}-196 a^{2}=0$$. Тогда a=0(не может быть) член $$a=\pm \frac{14\sqrt{3}}{3}$$ ( отрицательным не может быть )
3) $$KQ=CD \sin 60$$; $$CD=\sqrt{DH^{2}+CH^{2}}=\sqrt{64+((\sqrt{\frac{14^{2}}{3}-9}-\sqrt{(\frac{14^{2}}{3}-25)})^{2}}=$$$$\sqrt{64+(\frac{13}{\sqrt{3}}-\frac{11}{\sqrt{3}})^{2}}=\sqrt{\frac{196}{3}}=$$$$\frac{14}{\sqrt{3}}\Rightarrow$$ $$KQ=\frac{14}{\sqrt{3}}*\frac{\sqrt{3}}{2}=7$$$$\Rightarrow$$ $$MQ=13$$
4) $$S_{ABCD}=MQ*CD=13*\frac{14}{\sqrt{3}}=\frac{182}{\sqrt{3}}$$
Б) 1) из $$\Delta CHD$$: $$\sin \angle DCH=\frac{DH}{CD}=\frac{8}{\frac{14}{\sqrt{3}}}=\frac{4\sqrt{3}}{7}$$$$\Rightarrow$$ $$\sin \angle ADC=\frac{4\sqrt{3}}{7}=\sin \alpha$$
2) $$\angle ODQ=\frac{1}{2} \angle KDC=30$$$$\Rightarrow$$ $$\angle PDO=\angle (\alpha -30)$$, где $$\angle \alpha =\angle ADC$$; $$\cos \alpha =\sqrt{1-\sin ^{2}\alpha }=\frac{1}{7}$$; $$\sin (\alpha -30)=\sin \alpha \cos 30-\cos \alpha \sin 30=$$$$\frac{4\sqrt{3}}{7}*\frac{\sqrt{3}}{2}-\frac{1}{7}*\frac{1}{2}=$$$$\frac{11}{14}\Rightarrow$$ $$\cos(\alpha -30)=\frac{5\sqrt{3}}{14}$$
3) OD - радиус описанной окружности $$\Rightarrow$$ $$OD=\frac{2}{3}$$; $$KQ=\frac{2*7}{3}=\frac{14}{3}$$$$\Rightarrow$$ из $$\Delta EDO$$: $$ED=DO \cos PDO=\frac{14}{3}*\frac{5\sqrt{3}}{14}=$$$$\frac{5\sqrt{3}}{3}\Rightarrow$$ $$PD=\frac{10\sqrt{3}}{3}$$
4) $$S_{ABCD}=\frac{182}{\sqrt{3}}=AD*DH\Rightarrow$$ $$AD=\frac{182}{\sqrt{3}*8}=\frac{91}{4\sqrt{3}}\Rightarrow$$ $$AP=\frac{91}{4\sqrt{3}}-\frac{10}{\sqrt{3}}=\frac{51}{4\sqrt{3}}$$, $$\frac{AP}{AD}=\frac{51}{4\sqrt{3}}:\frac{91}{4\sqrt{3}}=\frac{51}{91}$$
Задание 6926
Даны треугольник АВС и ромб BDEF, все вершины которого лежат на сторонах треугольника АВС, а угол при вершине Е – тупой, АЕ=3, СЕ=7, а радиус окружности, вписанной в ромб, равен 1.
A) 1)Пусть r - радиус вписанной окружности в ромб (r=1); $$EG\perp AB$$; $$EH\perp CB$$. Тогда $$EG=EH=2r=2$$(высота в 2 раза больше радиуса в ромбе) .
2)из $$\Delta AEG$$: $$\sin A=\frac{EG}{AE}=\frac{2}{3}$$$$\Rightarrow$$ $$\cos A=\frac{\sqrt{5}}{3}$$
Из $$\Delta ECH$$: $$\sin C=\frac{EH}{EC}=\frac{2}{7}$$$$\Rightarrow$$ $$\cos C=\frac{\sqrt{45}}{7}=\frac{3\sqrt{5}}{7}$$
Из $$\Delta ACB$$: $$\sin B=\sin (180-(A+C))=\sin (A+C)$$
$$\sin (A+C)=\sin A* \cos C+\sin C*\cos A=$$$$\frac{2}{3}*\frac{3\sqrt{5}}{7}+\frac{2}{7}*\frac{\sqrt{5}}{3}=$$$$\frac{8\sqrt{5}}{21}\Rightarrow$$ $$\cos (A+C)=-\frac{11}{21}$$ ($$\angle A+\angle C>90$$)
3)По т. cинусов : $$\frac{AB}{\sin C}=\frac{AC}{\sin B}\Rightarrow$$ $$AB=10*\frac{2}{7}:\frac{8\sqrt{5}}{21}=\frac{3\sqrt{5}}{2}$$
4) $$S_{ABC}=\frac{1}{2}*AB*AC* \sin A=5\sqrt{5}$$
Б) 1) По т. синусов : $$\frac{AB}{\sin C}=\frac{BC}{\sin A}=\frac{AC}{\sin B}$$$$\Rightarrow$$ $$AB=\frac{AC*\sin C}{\sin B}=\frac{3\sqrt{5}}{2}$$; $$BC=\frac{AC* \sin A}{\sin B}=\frac{7\sqrt{5}}{2}$$. Тогда $$p=\frac{AB+AC+BC}{2}=\frac{10+5\sqrt{5}}{2}$$
2) Пусть $$R=KO_{1}$$ - радиус вписанной в $$\Delta ABC$$ $$\Rightarrow$$ $$R=\frac{S}{p}=10-4\sqrt{5}$$
3) $$\angle KBO=\frac{\angle B}{2}\Rightarrow$$ $$\cos \angle B=1-2 \sin ^{2}\angle KBO\Rightarrow$$ $$\sin \angle KBO=\frac{4}{\sqrt{21}}$$
4) из $$\Delta KO_{1}B$$: $$BO_{1}=\frac{O_{1}K}{\sin \angle KBO}=\frac{(10-4\sqrt{5})\sqrt{21}}{4}$$
Из $$\Delta NOB$$: $$OB=\frac{ON}{\sin \angle KBO}=\frac{\sqrt{21}}{4}$$
$$OO_{1}=BO_{1}-BO=\frac{\sqrt{21}}{4}(10-4\sqrt{5}-1)=\frac{\sqrt{21}}{4}(9-4\sqrt{5})$$
Задание 7109
В треугольнике АВС длина АВ равна 3, $$\angle ACB=\arcsin \frac{3}{5}$$ , хорда KN окружности, описанной около треугольника АВС, пересекает отрезки АС и ВC в точках M и L соответственно. Известно, что $$\angle ABC=\angle CML$$ , площадь четырехугольника ABLM равна 2, а длина LM равна 1.
A) $$\angle C$$ – общий ; $$\angle ABC =\angle CML\Rightarrow$$ $$\Delta ABC\sim \Delta CML$$: $$\frac{MC}{BC}=\frac{CN}{AC}=\frac{MN}{AB}=\frac{1}{3}\Rightarrow$$ $$S_{MCN}=(\frac{1}{3})^{2} S_{ABC}\Rightarrow$$ $$S_{AMNB}=\frac{8}{9}S_{ABC}\Rightarrow$$ $$S_{ABC}=\frac{9 S_{AMNB}}{8}=\frac{9}{4}$$$$\Rightarrow$$ $$S_{MCN}=\frac{1}{4}=\frac{1}{2} MN*h$$ ,где h-высота из $$C\Rightarrow h=\frac{1}{2}$$
Б) 1) Пусть O - центр описанной около $$\Delta ABC$$ окружности , тогда $$OC=OB=OA$$ - радиусы и $$OC=\frac{AB}{2 \sin ACB}=\frac{5}{2}$$
2) Пусть $$\angle ABC=\alpha \Rightarrow$$ $$\smile AC=2\alpha$$ (вписанный угол) и $$\angle LMC=\alpha$$ .
3) $$\angle LMC$$ - угол между хордами AC и KN $$\Rightarrow$$ $$\frac{\smile AK+\smile CN}{2}=\alpha \Rightarrow$$ $$\smile AK+\smile CN=2\alpha$$. При этом $$\smile AC=\smile AK+\smile KC=2\alpha \Rightarrow$$ $$\smile CN=\smile KC\Rightarrow$$ $$KC=CN$$
4) Пусть $$OC\cap KN=D\Rightarrow$$ $$CD=h=\frac{1}{2}$$( расстояние от C до ML ) $$\Rightarrow$$ $$OD=OC-DC=\frac{5}{2}-\frac{1}{2}=2\Rightarrow$$ $$KD=\sqrt{OK^{2}-OD^{2}}=1,5\Rightarrow$$ $$KN=3\Rightarrow$$ $$S_{KCN}=\frac{1}{2}*CD*KN=\frac{3}{4}$$
Задание 7182
A) 1) $$\angle KBL=\angle ADL=45$$ (угол между диагональю и стороной квадрата);
$$\angle HBT=\angle TDA$$ (накрест лежащие )$$\Rightarrow$$ $$\angle KBT=\angle TDL$$;
$$\angle BTK=\angle LTD$$ (вертикальные )$$\Rightarrow$$ $$\Delta KBT\sim \Delta TDL$$$$\Rightarrow$$ $$\angle BKT=\angle TLD$$
2) из $$\angle KBT=\angle NDL\Rightarrow$$ $$BK\left | \right |LD$$ $$\Rightarrow$$ $$\angle BKT=\angle TLD$$, то они накрест лежащие $$\Rightarrow$$ $$KT\left | \right |TL$$ или $$K,T,L \in KL$$, но параллельны быть не могут (так как имеют общую точку) $$\Rightarrow$$ KL-секущая
Б) 1) Аналогично п. A $$\Delta RCT \sim TAN$$ ($$\angle C=90$$; $$\angle BCD=\angle TAD$$ - накрест лежащие )$$\Rightarrow$$ $$AN\left | \right |RC$$; $$\angle TNA=\angle TRC$$$$\Rightarrow$$ $$R,T,N \in RN$$
2) из подобия : $$\frac{AN}{RC}=\frac{NT}{TR}\Leftrightarrow$$ $$\frac{8}{3}=\frac{20}{x}\Rightarrow$$ $$x=\frac{3*20}{8}=7,5\Rightarrow$$ $$RN=27,5$$
Задание 7325
Отрезок KB является биссектрисой треугольника KLM. Окружность радиуса 5 проходит через вершину KB, касается стороны LM в точке B и пересекает сторону KL в точке A . Известно, что $$ML=9\sqrt{3}$$, $$KA:LB=5:6$$
A) 1) Пусть KC пересекает окружность в C.
2) По свойству хорды и секущей $$\angle ABL=\angle AKB$$; $$\angle BKC=\angle CAB$$; т.к. KB – биссектриса, то $$\angle AKB=\angle BKC \Rightarrow$$ $$\angle ABL=\angle BAC\Rightarrow$$ $$LM\left \| \right \|AC$$
3) Пусть $$AK=5x$$ $$\Rightarrow$$ $$LB=6x$$, $$AL=y$$, тогда свойству секущей и хорды : $$AL*LK=LB^{2}\Rightarrow$$ $$y(y+5x)=(6x^{2})\Rightarrow$$ $$y^{2}+5xy-36y^{2}\Rightarrow$$ $$D=(5x)^{2}+4*36x^{2}=(13x)^{2}\Rightarrow$$ $$y_{1}=4x , y_{2}<0$$
4) $$\frac{AK}{AL}=\frac{5}{4}\Rightarrow$$ $$\frac{AK}{KL}=\frac{5}{9}=\frac{AC}{LM}\Rightarrow$$ $$AC=\frac{5}{9} *9\sqrt{3}=5\sqrt{3}$$
5) из $$\Delta AKC$$: $$\frac{AC}{\sin \angle AKC}=2 R$$ , $$R =5\Rightarrow$$ $$\sin \angle AKC=\frac{5\sqrt{3}}{2*5}=$$$$\frac{\sqrt{3}}{2}\Rightarrow$$ $$\angle AKC=60$$ или 120 (120 не может, т.к. $$\frac{AK}{AL}$$ должно быть тогда < 1)
Б) 1) Пусть $$KC=5t\Rightarrow$$ $$CM=4t\Rightarrow$$ по свойству биссектрисы $$BM=6t\Rightarrow$$ $$ML=6(x+t)=9\sqrt{3}\Rightarrow$$ $$x+t=\frac{3\sqrt{3}}{2}$$
2) из $$\Delta KLM$$: $$LM^{2}=LK^{2}+KM^{2}-2 LM*KM*\cos LKM\Leftrightarrow$$ $$(6(x+t))^{2}=81x^{2}+81t^{2}-81xt\Leftrightarrow$$ $$36x^{2}+36t^{2}+72xt=81x^\Leftrightarrow$$ $$2+81t^{2}-81xt\Leftrightarrow$$ $$5x^{2}+5t^{2}-17 xt=0\Leftrightarrow$$ $$5(x+t)^{2}=27xt\Leftrightarrow$$ $$5(\frac{3\sqrt{3}}{2})^{2}=27xt\Leftrightarrow$$ $$xt=\frac{5}{4}$$
3) $$S_{LKM}=\frac{1}{2} LK*KM*\sin LKM\Rightarrow$$ $$S_{LKM}=\frac{1}{2}*9x*9t*\frac{\sqrt{3}}{2}=$$$$\frac{81xt\sqrt{3}}{4}=\frac{405\sqrt{3}}{16}$$
Задание 7516
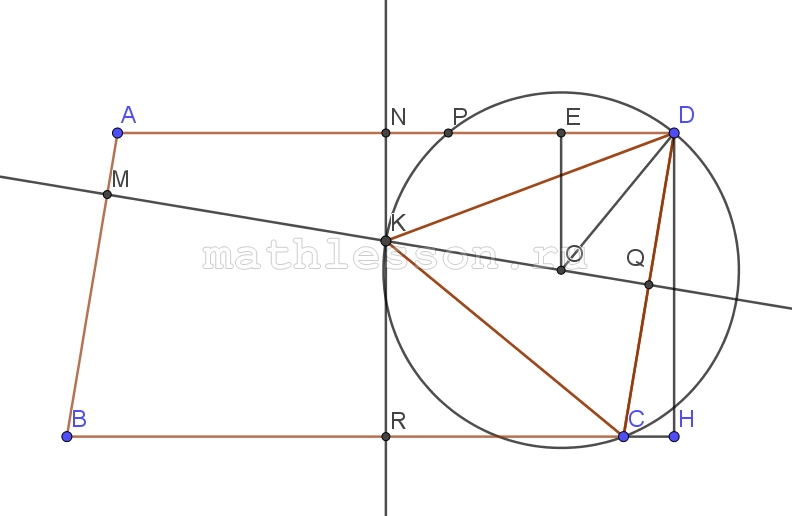
В трапеции ABCD с меньшим основанием ВС и площадью, равной 2, прямые ВС и AD касаются окружности диаметром $$\sqrt{2}$$ в точках В и D соответственно. Боковые стороны трапеции АВ и CD пересекают окружность в точках М и N соответственно. Длина MN равна 1.
Задание 10098
Два одинаковых правильных треугольника АВС и CDE расположены на плоскости так, что имеют только одну общую точку С, и угол BCD меньше, чем $$\frac{\pi}{3}$$. Точка К – середина отрезка АС, точка L – середина отрезка СЕ, точка М – середина отрезка BD.
Задание 10170
Биссектриса острого угла А трапеции ABCD пересекает боковую сторону CD в точке Т, а продолжение основания ВС трапеции в точке К так, что ABKD – параллелограмм и TD:TC=4:1
Задание 10289
В трапеции ABCD (AD – нижнее основание) площади треугольников ABD и BDC равны соответственно 12 и 4, а точка G является серединой BD. Ниже прямой AD выбрана точка Е, АЕ=BD, а на отрезке ЕС выбрана точка F такая, что CF в 4 раза короче СЕ.
Задание 10443
На гипотенузе KL равнобедренного прямоугольного треугольника KLM вне треугольника построен квадрат KLPQ. Прямая MQ пересекает гипотенузу KL в точке N.