ЕГЭ Профиль
Задание 6230
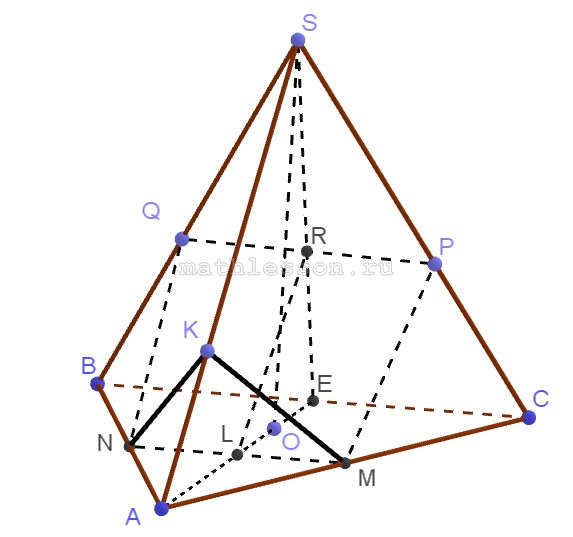
В правильной четырехугольной пирамиде SABCD с вершиной S AD=1/5 SD=1. Через точку В проведена плоскость $$\alpha$$ , пересекающая ребро SC в точке Е и удаленная от точек А и С на одинаковое расстояние, равное 1/10. Известно, что плоскость $$\alpha$$ не параллельна прямой АС.
A) 1) из $$\Delta ABC: AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{(\frac{1}{5})^{2}+(\frac{1}{5})^{2}}=\frac{\sqrt{2}}{5}$$, $$CH=\frac{1}{2}AC=\frac{\sqrt{2}}{10}$$
2)из $$\Delta HMC : \sin MHC=\frac{MC}{OH}=\frac{1}{2}:\frac{\sqrt{2}}{10}=\frac{\sqrt{2}}{2}\Rightarrow \angle MHC=45\Rightarrow$$ HE-биссектриса
3) из $$\Delta SHC: SH=\sqrt{SC^{2}-HC^{2}}=\sqrt{1-\frac{2}{100}}=\frac{\sqrt{98}}{10}$$
По свойству биссектрисы : $$\frac{SH}{HC}=\frac{SE}{EC}\Rightarrow \frac{\sqrt{98}}{10}:\frac{\sqrt{2}}{10}=\sqrt{\frac{98}{2}}=\frac{7}{1}$$
Б) 1)Пусть $$EH\perp HC$$,тогда из подобия $$\Delta SHC$$ и $$\Delta ENC :\frac{SE}{SC}=\frac{HN}{HC}\Rightarrow HN=\frac{SE*HC}{SC}=\frac{7*\frac{\sqrt{2}}{10}}{8}=\frac{7\sqrt{2}}{80}$$
2) $$S_{DNB}=\frac{1}{2}NH*DB=\frac{1}{2}*\frac{7\sqrt{2}}{80}*\frac{\sqrt{2}}{5}=\frac{7}{400}$$
3) $$S_{DEB}=\frac{S_{DNB}}{\cos EHC}=\frac{\frac{7}{400}}{\frac{\sqrt{2}}{2}}=\frac{7\sqrt{2}}{400}$$
Задание 6326
Основанием прямой призмы АВСА1В1С1 является равнобедренный треугольник АВС, в котором $$AC=CB=2$$ ,$$\angle ACB=2\arcsin \frac{4}{5}$$. Плоскость, перпендикулярная прямой А1В, пересекает ребра АВ и А1В1 в точках К и L соответственно, причем $$AK=\frac{7}{16}AB$$, $$LB_{1}=\frac{7}{16}A_{1}B_{1}$$ .
(Чтобы построить сечение, нужно будет проводить $$N_{1}O$$ до пересечения с $$BC$$ в точке F, и соединять KF)
A) 1)$$\angle ACB=2 \arcsin \frac{4}{5}\Rightarrow$$ $$\sin \angle ACB =\sin (2 \arcsin \frac{4}{5})=$$$$2\sin (\arcsin \frac{4}{5})\cos(\arcsin \frac{4}{5})=$$$$2\frac{4}{5}-\sqrt{1-(\frac{4}{5})^{2}}=$$$$\frac{8}{5}*\frac{3}{5}=\frac{24}{25}$$. Учитываем, что угол $$\arcsin$$ которого составляет $$\frac{4}{5}$$ больше $$\in (45;90)$$. Следовательно, двойной угол будет $$\in (90;180)$$, то есть его косинус отрицательный: $$\cos \angle ACB=-\sqrt{1-(\frac{24}{25})^{2}}=-\frac{7}{25}$$
2) $$A_{1}B_{1}=\sqrt{C_{1}A_{1}^{2}+C_{1}B_{1}^{2}-2C_{1}A_{1}*C_{1}B_{1}*\cos A_{1}C_{1}B_{1}}=$$$$\sqrt{2^{2}+2^{2}+2*2^{2}*\frac{7}{25}}=\frac{16}{5}$$
3) $$AK=\frac{7}{16}AB=\frac{7}{16}*\frac{16}{5}=\frac{7}{5}$$; $$KB=\frac{9}{16}*\frac{16}{5}=\frac{9}{5}$$; $$B_{1}L=\frac{7}{5}$$; $$LA_{1}=\frac{9}{5}$$; $$K_{1}M_{1}=B_{1}M_{1}-LB_{1}=\frac{8}{5}-\frac{7}{5}=\frac{1}{5}=MK$$
$$LM_{1}\left | \right |KM$$ и $$MM_{1}\perp AB A_{1}B_{1}\Rightarrow$$ $$\Delta LM_{1}O_{1}=\Delta O_{1}MK\Rightarrow M_{1}O_{1}=O_{1}K$$, но $$LN_{1}\left | \right |KN\left | \right |OO_{1}\Rightarrow C_{1}O=OC$$
Б) 1) $$O_{1}L\perp N_{1}L$$ т.к. $$M_{1}L\perp N_{1}L$$ (теорема о трех перпендикулярах)
$$B_{1}L=\frac{7}{5}\Rightarrow$$ $$\frac{B_{1}L}{B_{1}M_{1}}=\frac{7}{5}*\frac{5}{8}=\frac{7}{8}\Rightarrow$$ $$N_{1}L=\frac{7}{8}C_{1}M_{1}=\frac{7}{8}OO_{1}\Rightarrow$$ $$S_{OO_{1}LN_{1}}=\frac{OO_{1}+\frac{7}{8}OO_{1}}{2}*O_{1}L=\frac{15}{16}OO_{1}*O_{1}L$$ (так как имеем прямоугольную трапецию)
$$O_{1}L\perp N_{1}L$$ т.к. $$M_{1}L\perp N_{1}L$$ (теорема о трех перпендикулярах)
2) из $$\Delta LO_{1}A_{1}:$$ $$O_{1}M_{1}=\sqrt{LM_{1}*M_{1}A_{1}}=\sqrt{\frac{1}{5}*\frac{8}{5}}=\frac{2\sqrt{2}}{5}$$
$$K_{1}O_{1}=\sqrt{(\frac{1}{5})^{2}+(\frac{2\sqrt{2}}{5})^{2}}=\sqrt{\frac{1}{25}+\frac{8}{25}}=\frac{3}{5}$$
$$OO_{1}=C_{1}M_{1}=\sqrt{2^{2}-(\frac{8}{5})^{2}}=\sqrt{4-\frac{64}{25}}=\frac{6}{5}$$
3) Тогда площадь всего сечения есть удвоенная $$S_{OO_{1}LN_{1}}$$: $$S=\frac{15}{16}*\frac{6}{5}*\frac{3}{5}*2=1,35$$
Задание 6373
Через середину ребра АС правильной треугольной пирамиды SABC (S – вершина) проведены плоскости $$\alpha$$ и $$\beta$$ , каждая из которых образует угол 300 с плоскостью АВС. Сечения пирамиды этими плоскостями имеют общую сторону длины 1, лежащую в грани АВС, а плоскость $$\alpha$$ перпендикулярна ребру SA.
A) 1) AE- медиана $$\Rightarrow AE\perp NM\Rightarrow$$ $$NM\perp AS$$(теорема о трёх перпендикулярах )$$\Rightarrow (MNK)=\alpha$$
2) $$S_{MNC}=S_{NMA}*\cos30$$
$$MN=1\Rightarrow$$ $$CB=2\Rightarrow$$ $$S_{AMN}=\frac{1}{4}*S_{ABC}=$$$$\frac{1}{4}*\frac{1}{2}*2*2*\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$$
$$S_{MNK}=\frac{\sqrt{3}}{4}*\frac{\sqrt{3}}{2}=\frac{3}{8}$$
Б) 1) $$\beta \cap ABC=MN\Rightarrow$$ т.к. $$(BSK)\cap ABC=BC$$, то $$MN\left | \right |QP\Rightarrow QPMN$$ - равнобокая трапеция
2) $$\angle SAE=90-30=60(\Delta KLA)$$
$$\Delta ABC:AE=AC*\sin 60=$$$$\frac{\sqrt{3}}{2}*2=\sqrt{3}$$
$$AD=\frac{2}{3}AE=\frac{2\sqrt{3}}{3}$$, $$\Delta ASO:AS=\frac{AO}{\cos 60}=$$ $$\frac{2\sqrt{3}}{3}*2=\frac{4\sqrt{3}}{3}$$
3) $$\angle LRE=30$$, пусть AF –биссектриса $$SAE\Rightarrow AF\left | \right |LR$$, $$LR=\frac{1}{2}AF(\Delta AFE)$$
$$AF=\frac{2*AE*AS}{AE+AS}*\cos \frac{SAE}{2}=$$$$\frac{2\sqrt{3}*\frac{4\sqrt{3}}{3}}{\sqrt{3}+\frac{4\sqrt{3}}{3}}*\frac{\sqrt{3}}{2}=$$$$\frac{12}{7}\Rightarrow LR=\frac{6}{7}$$
4) По свойству биссектрисы: $$\frac{SF}{FE}=\frac{SA}{AE}=\frac{4}{3}$$
$$RE=FR=\frac{1}{2}FE=$$$$\frac{1}{2}*\frac{3}{7}AE=$$$$\frac{3}{14}SE$$
$$PQ=\frac{11}{12}BC=\frac{11}{7}\Rightarrow$$ $$S_{\beta}=\frac{1+\frac{11}{7}}{2}*\frac{6}{7}=\frac{54}{49}$$
Задание 6468
В основании четырехугольной пирамиды SABCD лежит квадрат со стороной 1. Ребро SA перпендикулярно плоскости основания и равно 2. Через вершину А параллельно диагонали BD проведено сечение, которое делит ребро SC в отношении 1:2, считая от вершины.
A) 1) по т. Менелая из $$\Delta CLA:$$ $$\frac{SK}{KO}*\frac{OA}{AC}*\frac{CL}{LS}=1\Leftrightarrow$$ $$\frac{SK}{KO}*\frac{1}{2}*\frac{2}{1}=1\Leftrightarrow$$ $$\frac{SK}{KO}=1\Leftrightarrow$$ $$SK=KO$$
Б) 1) $$AC\perp BD$$( ABCD - квадрат), но AC-проекция AL на (ABCD)$$\Rightarrow$$ $$AL\perp BD$$
2) $$MN\left | \right |BD\Rightarrow$$ $$AL\perp MN$$, $$S_{AMLN}=\frac{1}{2}AL*MN$$
3) из $$\Delta ACD$$: $$AC=\sqrt{1^{2}+1^{2}}=\sqrt{2}$$
Из $$\Delta ACS$$: $$CS=\sqrt{(\sqrt{2})^{2}+2^{2}}=\sqrt{6}$$
Тогда $$\cos \angle SCA=\frac{AC}{CS}=$$$$\frac{\sqrt{2}}{\sqrt{6}}=\frac{1}{\sqrt{3}}$$
$$LC=\frac{2}{3}CS=\frac{2\sqrt{6}}{3}$$
Из $$\Delta ACL$$: $$AL=\sqrt{(\sqrt{2})^{2}+(\frac{2\sqrt{6}}{3})^{2}-2\sqrt{2}*\frac{2\sqrt{6}}{3}*\frac{1}{\sqrt{3}}}=$$$$\sqrt{2+\frac{8}{3}-\frac{8}{3}}=\sqrt{2}$$
Из $$\Delta SBD\sim \Delta SNM$$: $$\frac{MN}{BD}=\frac{SK}{SO}=$$$$\frac{1}{2}\Rightarrow$$ $$MN=\frac{1}{2}BD=\frac{\sqrt{2}}{2}$$
4) $$S_{AMLN}=\frac{1}{2}*\frac{\sqrt{2}}{1}*\frac{\sqrt{2}}{2}=\frac{1}{2}$$
Задание 6522
Правильная треугольная призма АВСА1В1С1 пересечена плоскостью, проходящей через середины ребер АВ, А1С1, ВВ1. Сторона основания призмы равна 2, а высота призмы равна $$\frac{\sqrt{7}}{7}$$ .
A) 1) Введем ортогональную систему координат, как на рисунке .
2) Зададим уравнение плоскости сечения. Для этого найдем координаты трех точек, лежащих в данной плоскости:
$$N_{x}=-\frac{1}{2}KA=-\frac{1}{2};$$ $$N_{y}=\frac{1}{2}KB=\frac{\sqrt{3}}{2}$$; $$N_{z}=0$$
$$K_{x}=0$$; $$K_{y}=0$$; $$K_{z}=CC_{1}=\frac{\sqrt{7}}{7}$$
$$M_{x}=0$$; $$M_{y}=KB=\sqrt{3}$$; $$M_{z}=\frac{1}{2}CC_{1}=\frac{\sqrt{7}}{14}$$
Тогда : $$\left\{\begin{matrix}-\frac{1}{2}a+\frac{\sqrt{3}}{2}b+d=0\\\frac{\sqrt{7}}7{c+d=0}\\\sqrt{3}b+\frac{\sqrt{7}}{14}=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{1}{2}a+\frac{\sqrt{3}}2{b+d=0}\\c=-\sqrt{7}d\\\sqrt{3}b-\frac{7d}{14}+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}-\frac{1}{2}a-\frac{1}{4}d+d=0\\c=-\sqrt{7}d\\b=-\frac{1}{2\sqrt{3}}d\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a=\frac{3}{2}d\\b=-\frac{1}{2\sqrt{3}}d\\c=-\sqrt{7}d\end{matrix}\right.$$
Тогда нормаль-вектор для $$(NMK_{1})$$: $$\bar{n}(\frac{3}{2};-\frac{1}{2\sqrt{3}}; -\sqrt{7})$$
Нормаль-вектор для (ABC)-ось OZ: $$\bar{m}(0;0;1)$$
3) $$\cos(\bar{n},\bar{m})=\frac{\left | \frac{3}{2}*0-\frac{1}{2\sqrt{3}}*0-\sqrt{7}*1 \right |}{\sqrt{(\frac{3}{2})^{2}+(-\frac{1}{2\sqrt{3}})^{2}+(-\sqrt{7})^{2}}\sqrt{1^{2}}}=$$$$\frac{\sqrt{3}}{2}\Rightarrow$$ $$\angle (\bar{n},\bar{m})=30$$, что так же является углом между плоскостями
Б) 1) AN=NB; $$\angle ANE=\angle MNB\Rightarrow$$ $$\Delta ANE=\Delta NMB$$ и $$AE=MB=\frac{1}{2} BB_{1}=\frac{\sqrt{7}}{14}$$
2) $$\Delta ALE\sim \Delta A_{1}EK_{1}\Rightarrow$$ $$\frac{AL}{A_{1}K_{1}}=\frac{AE}{A_{1}E}=\frac{1}{3}\Rightarrow$$ $$AL=\frac{1}{3}\Rightarrow$$$$S_{\Delta ALN}=\frac{1}{2}*\frac{1}{3}*1*\frac{\sqrt{3}}{2}=$$$$\frac{\sqrt{3}}{12}(\frac{1}{2}AL*AN\sin A)$$
3)Проведем из B прямую $$\left | \right |NL\Rightarrow BQ$$: $$\frac{AN}{NB}=\frac{AL}{LQ}\Rightarrow$$ $$LQ=AL=\frac{1}{3}\Rightarrow$$ $$QK=1-2*\frac{1}{3}=\frac{1}{3}$$
4) $$\Delta KCR\sim \Delta QCB($$R-проекция $$R_{1}$$, $$K_{1}R_{1}\left | \right |KR$$, но $$K_{1}R_{1}\left | \right |LN\Rightarrow$$ $$K_{1}R_{1}\left | \right |QB\Leftrightarrow$$ $$KR\left | \right |QB$$)$$\Rightarrow S_{KCR}=S_{QCB}$$($$\frac{CK}{CQ})^{2}$$. $$S_{QCB}=\frac{1}{2}*\frac{4}{3}*2*\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}$$. $$(\frac{CK}{CQ})^{2}=(\frac{1}{\frac{4}{3}})^{2}=\frac{9}{16}$$. $$S_{KCR}=\frac{2\sqrt{3}}{3}*\frac{9}{16}=\frac{3\sqrt{3}}{8}$$
5) $$S_{\angle NBRK}=S_{ABC}-S_{ALN}-S_{CKR}$$
$$S_{ABC}=\frac{1}{2}*2*2*\frac{\sqrt{3}}{2}=\sqrt{3}$$
$$S_{\angle NBRK}=\sqrt{3}-\frac{\sqrt{3}}{12}-\frac{3\sqrt{3}}{8}=\frac{13\sqrt{3}}{24}$$
Но LNBRK-проекция $$K_{1}LNMR_{1}$$ на $$(ABC)\Rightarrow S_{K_{1}LNMR_{1}}=$$$$\frac{S_{\angle NBRK}}{\cos\alpha }$$,где $$\alpha =30$$
$$S_{K_{1}LNMR_{1}}=\frac{13\sqrt{3}}{24}:\frac{\sqrt{3}}{2}=\frac{13}{12}$$
Задание 6616
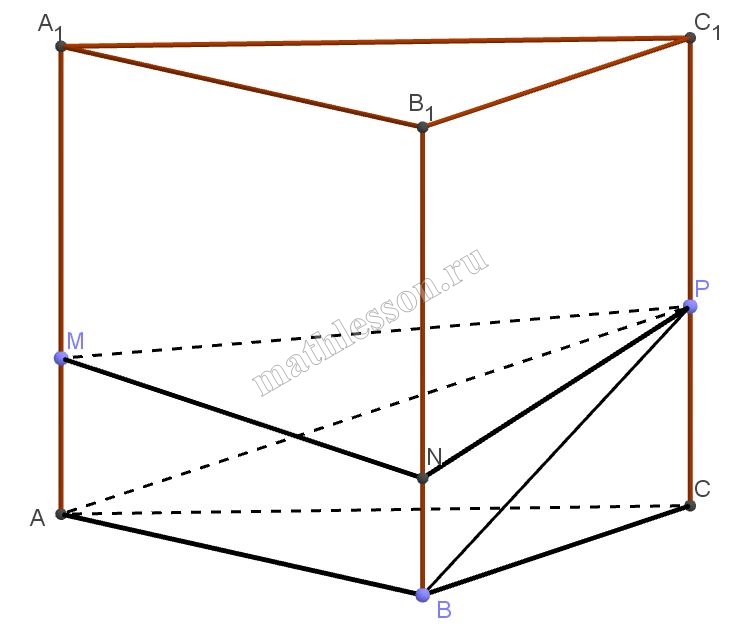
Точки M,N и P лежат на боковых ребрах правильной треугольной призмы ABCA1B1C1 и делят их в отношении $$AM:MA_{1}=1:2$$, $$BN:NB_{1}=1:3$$, $$CP:PC_{1}=2:3$$
A) 1) Пусть a - ребро основания, b - боковое ребро. Тогда: $$AM=\frac{1}{3}b$$, $$NB=\frac{1}{4}b$$, $$CP=\frac{2}{5}b$$
2) Разобъем многогранник ABCMNP на пирамиды : PABNM и PABC
3) Пусть $$CH\perp AB$$ и h - перпендикуляр из P. Тогда $$CH=h\Rightarrow$$ $$V_{PABNM}=\frac{1}{3}S_{ABNM}*CH$$. Из $$\Delta ABC$$: $$CH=AB *\sin 60=\frac{\sqrt{3}a}{2}$$
$$S_{ABNM}=\frac{AM+NB}{2}*AB=$$$$\frac{\frac{1}{3}b+\frac{1}{4}b}{2}*a=\frac{7ab}{24}$$
$$V_{PABNM}=\frac{1}{3}*\frac{7ab}{24}*\frac{\sqrt{3}a}{2}=$$$$\frac{7a^{2}b\sqrt{3}}{144}$$
4) $$V_{PABC}=\frac{1}{3}S_{ABC}*CP$$
$$S_{ABC}=\frac{1}{2}*AB*BC*\sin 60=$$$$\frac{\sqrt{3}a^{2}}{4}$$
$$V_{PABC}=\frac{1}{3}*\frac{\sqrt{3}a^{2}}{4}*\frac{2}{5}b=$$$$\frac{2\sqrt{3}a^{2}b}{60}$$
Тогда $$V_{ABCMNP}=\frac{7a^{2}b\sqrt{3}}{144}=$$$$\frac{2\sqrt{3}a^{2}b}{60}=$$$$\frac{(35+24)\sqrt{3}a^{2}b}{720}=\frac{59\sqrt{3}a^{2}b}{720}$$
5) $$V_{ABCA_{1}B_{1}C_{1}}=S_{ABC}*CC_{1}=$$$$\frac{\sqrt{3}a^{2}}{4}*b=\frac{\sqrt{3}a^{2}b}{4}$$
6) $$V_{A_{1}B_{1}C_{1}MNP}=$$$$\frac{\sqrt{3}a^{2}b}{4}-\frac{59\sqrt{3}a^{2}b}{720}=$$$$\frac{121\sqrt{3}a^{2}b}{720}$$
Тогда: $$\frac{V_{ABCMNP}}{V_{A_{1}B_{1}C_{1}MNP}}=\frac{59}{121}$$
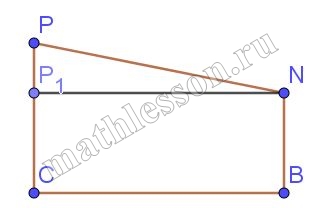
Б) 1) $$MN=AM-NB=5$$. $$NM_{1}\perp AM\Rightarrow$$ $$NM_{1}=AB=2\sqrt{10}$$
2) $$\Delta MNM_{1} MN=\sqrt{5^{2}+(2\sqrt{10}^{2})}=\sqrt{25+40}=\sqrt{65}$$
3) Аналогично $$PP_{1}=PC-NB=9$$. $$PN=\sqrt{81+40}=\sqrt{121}$$
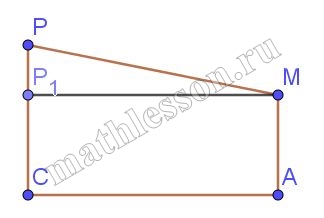
4) Аналогично : $$PM_{1}=24-20=4$$. $$MP=\sqrt{16+40}=\sqrt{56}$$
5) $$MN^{2}+MP^{2}=65+56=121=PN$$ - выполнилась теорема Пифагора
Задание 7019
В правильной треугольной пирамиде ABCD сторона основания АВС равна 12, $$\angle ADB=2 arctg \frac{3}{4}$$ . В треугольнике ABD проведена биссектриса ВА1, а в треугольнике BCD проведены медиана ВС1 и высота СВ1.
A) 1) Пусть DH-высота в $$\Delta ADB$$ $$\Rightarrow$$ $$\angle HDB =arctg\frac{3}{4}\Rightarrow$$ $$tg\angle HDB =\frac{3}{4}=\frac{HB}{DH}$$; $$HB=\frac{AB}{2}=6\Rightarrow$$ $$DH=8\Rightarrow$$ из $$\Delta DHB$$: $$DB=\sqrt{DH^{2}+HB^{2}}=10$$
2) $$\frac{V_{A_{1}B_{1}C_{1}D_{1}}}{V_{ABCD}}=$$$$\frac{A_{1}D*B_{1}D*C_{1}D}{AD*BD*CD}(1)$$
3) из $$\Delta ABD$$: $$\frac{AB}{BD}=\frac{AA_{1}}{A_{1}D}=\frac{12}{10}=\frac{6}{5}\Rightarrow$$ $$A_{1}D=\frac{5}{11}AD$$(по свойству биссектрисы)
4) $$DC_{1}=\frac{1}{2}DC$$ (медиана)
Из $$\Delta BCD$$: $$\cos D=\frac{BD^{2}+CD^{2}-BC^{2}}{2 *BD*CD}=0,28$$$$\Rightarrow$$
Из $$\Delta DB_{1}C$$: $$DB_{1}=0,28 DC\Rightarrow$$ $$DB_{1}=0,28DB$$
5) Пусть DO – высота ABCD.
Из $$\Delta ABC$$: $$CH=CB \sin B=12\frac{\sqrt{3}}2{}=6\sqrt{3}\Rightarrow$$ $$CO=\frac{2}{3} CH=4\sqrt{3}$$
Из $$\Delta DOC$$: $$DO=\sqrt{CD^{2}-OC^{2}}=\sqrt{10^{2}-(4\sqrt{3})^{2}}=\sqrt{52}$$
$$S_{ABC}=\frac{1}{2} *12^{2}*\frac{\sqrt{3}}{2}=36 \sqrt{3}$$
$$V_{ABCD}=\frac{1}{3}*36\sqrt{3}*\sqrt{52}=12\sqrt{156}$$
$$V_{A_{1}B_{1}C_{1}D_{1}}=\frac{5}{11}*\frac{1}{2}*\frac{28}{100}*12\sqrt{156}=$$$$\frac{42}{55}\sqrt{156}=\frac{84\sqrt{39}}{55}$$
Б) Пусть $$A_{1}^{'}$$, $$B_{1}^{'}$$, $$C_{1}^{'}$$ проекция $$A_{1}$$, $$B_{1}$$ и $$C_{1}$$ на (ABC). Тогда :
1) из $$\Delta DAO$$: $$\frac{DA_{1}}{DA}=\frac{OA_{1}^{'}}{OA}=\frac{5}{11}$$
2)из $$\Delta DOC$$: $$\frac{DC_{1}}{DC}=\frac{OC_{1}^{'}}{OC_{1}}=\frac{1}{2}$$
3) из $$\Delta DOB$$: $$\frac{DB_{1}}{DB}=\frac{DB_{1}^{'}}{OB}=\frac{28}{100}=\frac{7}{25}$$
4) $$\frac{S_{A_{1}^{'}OC_{1}^{'}}}{S_{AOC}}=$$$$\frac{OA_{1}^{'}*OC_{1}^{'}}{OA*OC}=$$$$\frac{5}{11}*\frac{1}{2}=\frac{5}{22}$$
$$\frac{S_{OC_{1}^{'}B_{1}^{'}}}{S_{OCB}}=\frac{OC_{1}^{'}*OB_{1}^{'}}{OC* OB}=$$$$\frac{1}{2}*\frac{7}{25}=\frac{7}{50}$$
$$\frac{S_{OA_{1}^{'}B_{1}^{'}}}{S_{OAB}}=\frac{OB_{1}^{'}*OA_{1}^{'}}{OB*OA}=$$$$\frac{7}{25}*\frac{5}{11}=\frac{7}{55}$$
$$S_{AOC}=S_{BOC}=S_{AOB}=\frac{1}{3}S_{ABC}\Rightarrow$$ $$S_{A_{1}^{'}B_{1}^{'}C_{1}^{'}}=\frac{1}{3}(\frac{5}{22}+\frac{7}{50}+\frac{7}{55})*36\sqrt{3}=$$$$12\sqrt{3}*\frac{125+77+70}{550}=$$$$12\sqrt{3}*\frac{272}{550}=\frac{1632\sqrt{3}}{275}$$
Задание 7107
В правильной шестиугольной пирамиде SABCDEF сторона основания ABCDEF равна 2, а боковое ребро 3.
A) 1) Соединим AM , через M проведем прямую $$a\left | \right |AF$$; $$a\cap SD=N\Rightarrow$$ $$MN\left | \right |AF$$
2) AC-проекция AM ; Пусть SR-высота в $$\Delta ASC$$; $$SR\cap AM =K \Rightarrow$$ через K пойдет прямая , параллельная AF ( по ней пересекаются сечение и (SEB) ); пусть она пересекает SE и SB в H и G соответственно , тогда (AGMNF)-искомое сечение
3) из $$\Delta AMC$$ и точки $$S \in GM$$ по т. Менелая : $$\frac{SK}{KR}=\frac{RA}{AC}*\frac{CM}{MS}=1$$; $$\Delta SAC$$ равнобедренный $$\Rightarrow$$ $$AR=RC\Rightarrow$$ $$\frac{SK}{KR}*\frac{1}{2}*\frac{1}{1}=1\Rightarrow$$ $$\frac{SC}{KR}=\frac{2}{1}(*)$$ ( можно сразу сказать , что K-точка пересечения медиан $$\Rightarrow$$ 2: 1)
4) $$\Delta SHG\sim \Delta SEB\Rightarrow$$ $$\Delta SGK\sim \Delta SBK\Rightarrow$$ $$\frac{SK}{KR}=\frac{SC}{SB}=\frac{2}{1}$$
Б) 1) Пусть SO-высота пирамиды $$\Rightarrow$$ из $$\Delta SOB$$: $$SO=\sqrt{SB^{2}-OB^{2}}=\sqrt{5}\Rightarrow$$ $$YO=\frac{1}{3} SO=\frac{\sqrt{5}}{3}$$;
2) из $$\Delta FOA$$: $$OZ=OA*\sin A=2*\frac{\sqrt{3}}{2}=\sqrt{3}\Rightarrow$$ из $$\Delta ZOY$$: $$ZY=\sqrt{ZO^{2}+OY^{2}}=\frac{\sqrt{32}}{3}\Rightarrow$$ $$\cos YZO=\frac{ZO}{ZY}=\frac{3\sqrt{3}}{\sqrt{32}}$$
3) Пусть $$AG^{'}M^{'}N^{'}H^{'}F$$- проекция сечения на (ABC) и $$S _{AC_{1}^{'}M^{'}N^{'}H^{'}F}=S_{1}$$. Пусть S-площадь сечения $$\Rightarrow$$ $$S=\frac{S_{1}}{\cos YZO}$$
4) $$S_{ZOA}=x=\frac{1}{2} *2*2*\frac{\sqrt{3}}{2}=\sqrt{3}$$;
$$S_{AOC_{1}^{'}}=S_{ZOH^{'}}=$$$$\frac{OC_{1}^{'}}{OB}*x=$$$$\frac{SC_{1}}{SB}*x=\frac{2}{3}x=\frac{2\sqrt{3}}{3}$$
Аналогично: $$S_{G^{'}OM^{'}}=S_{H^{'}ON^{'}}=$$$$\frac{2}{3}*\frac{1}{2}x=\frac{1}{3}x$$ и $$S_{N^{'}OM^{'}}=\frac{1}{4}x$$
Тогда $$S_{1}=\sqrt{3} (1+2*\frac{2}{3}+2*\frac{1}{3}+\frac{1}{4})=\frac{13\sqrt{3}}{4}$$
$$S=\frac{13\sqrt{3}}{4} :\frac{3\sqrt{3}}{\sqrt{32}}=$$$$\frac{13\sqrt{3}*4\sqrt{2}}{4*3\sqrt{3}}=$$$$\frac{13\sqrt{2}}{3}$$
Задание 7180
В основании пирамиды с вершиной S лежит прямоугольник, центр которого находится на высоте пирамиды. Плоскость пересекает боковые ребра пирамиды в точках P, Q, M и N так, что Р и М – противоположные вершины четырехугольника PQMN. Известно, что $$SP=7$$, $$SM=\frac{7}{6}$$, $$SQ+SN=\frac{25}{6}$$, $$SQ>SN$$
A) 1)Через P проведем плоскость параллельную (ABC): $$PQ_{1}M_{1}N{1})$$$$\Rightarrow$$ $$SP=SQ=SM_{1}=SN_{1}=7$$. Пусть H –центр ABCD $$\Rightarrow$$ SH –высота пирамиды; $$SH\cap (PQMN)=O$$, $$SH\cap (PQ_{1}M_{1}N_{1})=O_{1}$$ ; $$MM_{1}=SM_{1}-SM=\frac{35}{6}$$
2) Из $$\Delta SM_{1}P$$: $$M_{1}Q_{1}=O_{1}P\Rightarrow$$ по т. Менелая для $$\Delta MPM_{1}$$ : $$\frac{SO}{OO_{1}}*\frac{O_{1}P}{PM_{1}}*\frac{M_{1}M}{MS}=1\Leftrightarrow$$ $$\frac{SO}{OO_{1}}*\frac{1}{2}*\frac{35}{6}:\frac{7}{6}=1\Leftrightarrow$$ $$\frac{SO}{OO_{1}}=\frac{2}{5}$$
3) Рассмотрим $$\Delta SQ_{1}N_{1}$$: пусть $$SQ=x\Rightarrow$$ $$SN=\frac{25-x}{6}$$; Построим $$N_{2}Q_{2}\left | \right |N_{1}Q_{1}\Rightarrow$$ $$\Delta SON_{2}\sim \Delta SO_{1}N_{1}\Rightarrow$$ $$\frac{SN_{2}}{N_{2}N_{1}}=\frac{SO}{OO_{1}}=\frac{2}{5}$$. Т.е. $$SN_{1}=7$$, то $$SN_{2}=2=SQ_{2}$$, тогда $$N_{2}N=SN_{2}-SN=2-(\frac{25}{6}-x)=x-\frac{13}{6}$$; $$Q_{2}Q=SQ-SQ_{2}=x-2$$
По т. Менелая для $$\Delta NSQ$$: $$\frac{N_{2}O}{OQ_{2}}*\frac{Q_{2}Q}{QS}*\frac{SN}{NN_{2}}=1$$$$\Leftrightarrow$$ $$\frac{1}{1}*\frac{x-2}{x}*\frac{\frac{25}{6}-x}{x-\frac{13}{6}}=1$$$$\Leftrightarrow$$ $$(x-2)(\frac{25}{6}-x)=x(x-\frac{13}{6})|*6$$$$\Leftrightarrow$$ $$12x^{2}-50x+50=0\Leftrightarrow$$ $$6x^{2}-25x+25=0\Leftrightarrow$$ $$\left[\begin{matrix}x_{1}=\frac{5}{2}\\x_{2}=\frac{5}{3}\end{matrix}\right.$$
$$\frac{5}{3}$$ не подходит, т.к. $$\frac{25}{6}-\frac{5}{3}=\frac{5}{2}$$ и $$\frac{5}{3}<\frac{5}{2}$$, а по условию $$SQ>SN\Rightarrow$$ $$SQ=\frac{5}{2}$$; $$SN=\frac{5}{3}$$
Б) 1) Рассмотрим $$\Delta SHD$$: $$SQ_{2}=2$$; $$Q_{2}Q_{1}=5$$; $$Q_{1}D=SD-SQ_{1}=10-7=3\Rightarrow$$ $$Q_{2}D=5+3=8$$
2) $$\Delta SOQ_{2}\sim \Delta SHD\Rightarrow$$ $$\frac{SO}{OH}=\frac{SQ_{2}}{Q_{2}D}=\frac{2}{8}=\frac{1}{4}$$
Задание 7221
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=4, AD=6, AA1=8 . Точка К, лежащая на ребре АА1, удалена от вершины А на 4, расстояние от точки L, лежащей на ребре DD1 до вершины D равно 2. Точка М лежит на отрезке В1С, длина МС вдвое больше длины В1М.
A) 1) K и L лежат в одной плоскости $$\Rightarrow$$ соединяем .
2) $$(ADD_{1}) \left | \right |(BCC_{1})\Rightarrow$$ через M пройдет прямая , параллельная KL . Пусть она пересекает $$BB_{1}$$ , в N и $$CC_{1}$$ в R $$\Rightarrow$$ (KNRL)-искомое сечение.
3) Зададим уравнение (KNRL) : введем ортогональную систему координат, тогда: $$K(0;0;4)$$; $$L(6; 0; 2)$$; $$M(\frac{1}{3} AD; AB ; \frac{2}{3} BB_{1})$$$$\Rightarrow$$ $$M(2 ;4; \frac{16}{3})$$
Пусть $$ax+by+cz+d=0$$ - уравнение (KNRL), тогда: $$\left\{\begin{matrix}a*0+b*0+c*4+d=0\\a*6+b*0+c*2+d=0\\a*2+b*4+c*\frac{16}{3}+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}4c+d=0\\6a+2c+d=0\\2a+4b+\frac{16c}{3}+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}c=-\frac{d}{4}\\a=-\frac{d}{12}\\b=\frac{d}{8}\end{matrix}\right.$$
Получим : $$-\frac{d}{12}x+\frac{d}{8}y-\frac{d}{4}z+d=0$$$$\Leftrightarrow$$ $$2x-3y+6z-24=0$$. Следовательно, нормаль-вектор для (KNRL) : $$\bar{n}(2; -3; 6)$$ . Для ($$DCC_{1}$$) : $$\bar{AD}$$ или $$\bar{Ox}(1 ;0;0)$$
$$\cos (\bar{n};\bar{Ox})=\cos ((KNRL);(DCC_{1}))=$$$$\frac{\left | 2*1+(-3)*0+6*0 \right |}{\sqrt{2^{2}+(-3)^{2}+6^{2}}\sqrt{1^{2}+0^{2}+0^{2}}}=$$$$\frac{2}{7}\Rightarrow$$ угол между этими плоскостями $$\alpha =arccos \frac{2}{7}$$
Б) 1) Пусть S - площадь (KLM), $$S_{1}$$ - площадь ее проекции на (ABC)-это и будет ABCD. Найдем $$\cos ((KLM ); (ABC))$$: нормаль вектора для (ABC) - $$\vec{Oz}(0;0;1)$$, тогда $$\cos ((KLM) ;(ABC))=\cos (\vec{n}; \vec{Oz})=$$$$\frac{\left | 2*0+(-3)*0+6*1 \right |}{\sqrt{2^{2}+(-3)^{2}+6^{2}}\sqrt{1^{2}}}=$$$$\frac{6}{7}=\cos \beta$$
2) $$S=\frac{S_{1}}{\cos \beta }=$$$$\frac{AB*AD}{\cos \beta }=$$$$\frac{6*4}{\frac{6}{7}}=28$$
Задание 7561
Дан куб АВСDA1B1C1D1 с ребром длины 1. Точка Р – середина ребра А1D1, точка Q делит отрезок АВ1 в отношении 2:1, считая от вершины А, R – точка пересечения отрезков ВС1 и В1С.
Задание 7864
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4. Точки M и N – середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
a) 1) Пусть $$SO$$ - высота пирамиды, $$\bigtriangleup SOB$$ - прямоугольный. Пусть $$NH\parallel SO$$ $$\Rightarrow$$ $$NH\cap OB=H$$ и $$OH=HB$$ (т.к. $$NH$$ - средняя линия)
2) Проведем через $$H$$ прямую,параллельную $$MN$$ (т.к. плоскость пересекает двугранный угол). Пусть прямая пересекает $$CB$$ и $$CA$$ в $$L$$ и $$K$$ соответственно $$\Rightarrow$$ $$(MNLK)$$ - искомое сечение.
3) $$MN\parallel AB$$; $$MN\parallel LK$$ $$\Rightarrow$$ $$LK\parallel AB$$. Пусть $$LK\cap OE=R$$, тогда $$\frac{OR}{RE}=\frac{OH}{HB}=\frac{1}{1}$$. Но $$\frac{CO}{OE}=\frac{2}{1}$$ ($$CE$$ - середина) $$\Rightarrow$$ $$\frac{CR}{RE}=\frac{2OE+\frac{1}{2}OE}{\frac{1}{2}OE}=\frac{5}{1}$$
б) 1) $$MN=\frac{1}{2}AB=3$$; $$KL=\frac{5}{6}AB=5$$;
2) из $$\bigtriangleup SBC$$: $$\cos B=\frac{SB^{2}+CB^{2}-SC^{2}}{2SB\cdot CB}=\frac{4^{2}+6^{2}-4^{2}}{2\cdot6\cdot4}=\frac{3}{4}$$
3) $$HB=\frac{1}{6}CB=1$$ $$\Rightarrow$$ из $$\bigtriangleup NBL$$: $$NH=\sqrt{NB^{2}+BL^{2}-2NB\cdot BL\cdot\cos B}=\sqrt{2^{2}+1^{2}-2\cdot2\cdot1\cdot\frac{3}{4}}=\sqrt{4+1-3}=\sqrt{2}$$ $$\bigtriangleup AMK=\bigtriangleup NLB$$ по двум сторонам и углу между ними $$\Rightarrow$$ $$MK=NL$$
4) $$P=MN+KL+MK+NL=5+3+2\sqrt{2}=8+2\sqrt{2}$$
Задание 8237
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ребро основания АВ=2, высота АА1=6, точка М – середина F1E1, проведено сечение через точки А, С и М.
A) 1) Построим сечение: через $$M$$ проведем прямую $$a\parallel AC$$; $$a\cap E_{1}D_{1}=N$$ $$\Rightarrow$$ $$MN\parallel AC$$.
$$MN\cap C_{1}D_{1}=O_{2}$$; $$MN\cap A_{1}F_{1}=O_{1}$$; $$CO_{2}=\cap DD_{1}=K$$; $$AO_{1}\cap FF_{1}=L$$ $$\Rightarrow$$ $$(ACKNML)$$ - сечение
2) $$A_{1}C_{1}\parallel AC$$; $$AC\parallel MN$$ $$\Rightarrow$$ $$A_{1}C_{1}\parallel MN$$; $$F_{1}D_{1}\parallel MN$$ $$\Rightarrow$$ $$\bigtriangleup F_{1}E_{1}D_{1}\sim\bigtriangleup ME_{1}N$$ $$\Rightarrow$$ $$\frac{F_{1}N}{ME_{1}}=\frac{D_{1}N}{NE_{1}}=\frac{1}{1}$$
Б) 1) Опустим из $$R$$ перпендикуляр $$PR'$$ на $$(ABC)$$. Из $$\bigtriangleup HBC$$: $$\angle C=30^{\circ}$$ $$\Rightarrow$$ $$HB=\frac{BC}{2}=1$$; $$HC=\sqrt{3}$$; $$ER'=\frac{HB}{2}=0,5$$. $$EB=2AB=4$$ $$\Rightarrow$$ $$R'H=4-1-0,5=2,5$$
2) Из $$\bigtriangleup RR'H$$: $$RR'=DD_{1}=6$$ $$\Rightarrow$$ по т. Пифагора: $$RH=\sqrt{6^{2}+2,5^{2}}=6,5=CO_{2}$$
3) $$S_{ACKNML}=S=S_{CO_{2}O_{1}A}-2S_{NO_{2}K}$$ (т.к. $$\bigtriangleup NO_{2}K=\bigtriangleup MO_{1}L$$ по катету $$NO_{2}=MO_{1}$$ и острому углу $$\angle N=\angle M$$)
4) $$NO_{2}=RN=\frac{1}{2}HC=\frac{\sqrt{3}}{2}$$; $$O_{2}D_{1}=E_{1}R=\frac{1}{2}$$ $$\bigtriangleup O_{2}D_{1}K\sim\bigtriangleup DKC$$ $$\Rightarrow$$ $$\frac{D_{1}K}{KD}=\frac{O_{2}D_{1}}{DC}=\frac{\frac{1}{2}}{2}=\frac{1}{4}$$ $$\Rightarrow$$ $$D_{1}K=\frac{DD_{1}}{5}=\frac{6}{5}$$
Из $$\bigtriangleup O_{2}DK$$: $$O_{2}K=\sqrt{(\frac{1}{2})^{2}+(\frac{6}{5})^{2}}=\frac{13}{10}$$
Из $$\bigtriangleup NO_{2}K$$: $$S_{NO_{2}K}=\frac{1}{2}\cdot\frac{13}{10}\cdot\frac{\sqrt{3}}{2}=\frac{13\sqrt{3}}{40}$$
5) $$AC=2HC=2\sqrt{3}$$ $$\Rightarrow$$ $$S=2\sqrt{3}\cdot6,5-\frac{13\sqrt{3}}{40}\cdot2=\frac{247\sqrt{3}}{20}$$
Задание 8287
В правильной пирамиде SABC точки M и N –середины ребер АВ и ВС соответственно. На боковом ребре SA отмечена точка К, SK:KA=1:3. Сечение пирамиды плоскостью MNK является четырехугольником, диагонали которого пересекаются в точке Q.
а) Отрезок $$MN$$ является средней линией треугольника $$ABC$$, следовательно, $$MN||AC$$. Таким образом, сечение пересекает грань $$SAC$$ по прямой, также параллельной $$AC$$. Пусть $$L$$ — точка пересечения сечения с ребром $$SC$$, тогда $$KL||AC$$, а сечение $$KLMN$$ — равнобедренная трапеция.
Рассмотрим сечение пирамиды плоскостью $$BSH$$, где $$H$$ — середина стороны $$AC$$. Пусть $$R$$ и $$T$$ — середины оснований $$MN$$ и $$KL$$ трапеции соответственно. Тогда высота трапеции $$RT$$ проходит через точку $$Q$$ пересечения диагоналей трапеции, причём так как $$MN=\frac{1}{2}AC$$, а $$KL=\frac{1}{4}AC$$, из подобия треугольников $$KLQ$$ и $$MNQ$$, получаем $$\frac{TQ}{QR}=\frac{KL}{MN}=\frac{1}{2}$$. Отрезок $$TR$$ и высота пирамиды $$SO$$ лежат в плоскости $$BSH$$. Пусть они пересекаются в точке $$Q'$$. Докажем, что она совпадает с точкой $$Q$$.
В сечении $$BSH$$ проведём отрезок $$TW$$ параллельно $$BH$$, где $$W$$ — точка на высоте пирамиды. Треугольники $$TQ'W$$ и $$RQ'O$$ подобны.
При этом $$k'=\frac{TQ'}{Q'R}=\frac{TW}{RO}=\frac{\frac{1}{4}OH}{\frac{2}{3}BH-\frac{1}{2}BH}=\frac{\frac{1}{4}\cdot\frac{1}{3}BH}{\frac{1}{6}BH}=\frac{1}{2}$$.
Таким образом, дробь: $$\frac{TQ'}{Q'R}=\frac{TQ}{QR}$$ , а, значит, точки $$Q'$$ и $$Q$$ совпадают, и $$Q$$ лежит на высоте пирамиды $$SO$$.
б) Так как $$AC=2$$, то $$MN=1$$, а $$KL=\frac{1}{2}$$ .
Осталось найти высоту трапеции $$RT$$. Из пункта а) получаем, что $$\frac{WQ}{QO}=\frac{1}{2}$$ , при этом $$\frac{SW}{WO}=\frac{1}{3}$$ .
Следовательно, $$WQ=1$$, $$WT=\frac{1}{12}BH=\frac{\sqrt{3}}{12}$$.
Тогда $$RT=3QT=3\sqrt{1+\frac{3}{144}}=\frac{7\sqrt{3}}{4}$$.
Откуда $$S_{KLMN}=\frac{1}{2}(1+\frac{1}{2})\frac{7\sqrt{3}}{4}=\frac{21\sqrt{3}}{16}$$.
Задание 8343
Основанием четырехугольной пирамиды SABCD с равными боковыми ребрами является прямоугольник ABCD площадь которого равна 25. Плоскость, параллельная плоскости основания пересекает ребро AS в точке А1, а высоту пирамиды ‐ в середине О. Угол между гранями ADS и BCS равен 60 градусов.
А) 1) Пусть $$AC\cap BD=Q$$ $$\Rightarrow$$ по свойствам прямоугольника $$AQ=QC=QD=QB$$/ $$SA=SB=SC=SD$$; $$SQ$$ - общая $$\Rightarrow$$ $$\bigtriangleup SAQ=\bigtriangleup SBQ=\bigtriangleup SCQ=\bigtriangleup SDQ$$ по трем сторонам $$\Rightarrow$$ $$\angle SQD=\angle SQB=\angle SQA=\angle SQC=90^{\circ}$$ $$\Rightarrow$$ $$SQ$$ - высота $$SABCD$$
2) $$AD=BC$$ $$\Rightarrow$$ $$\bigtriangleup SDA=\bigtriangleup SBC$$ $$\Rightarrow$$ $$SL=SK$$ (где $$L$$ и $$K$$ - середины $$AD$$ и $$BC$$), но $$SL\perp AD$$ и $$LK\perp AD$$ $$\Rightarrow$$ $$AD\perp(SLK)$$ и $$(ADS)\perp(SLK)$$, аналогично $$(SBC)\perp(SLK)$$ $$\Rightarrow$$ $$\angle LSK=60^{\circ}$$ $$\Rightarrow$$ $$\bigtriangleup SLK$$ - равносторонний
3) $$SO=OQ$$ $$\Rightarrow$$ $$SL_{1}=L_{1}L$$ ($$\bigtriangleup SL_{1}K_{1}\sim\bigtriangleup SLK$$); $$L_{1}K_{1}$$ - средняя линия $$SLK$$ $$\Rightarrow$$ $$SQ$$ - медиана; $$KL_{1}$$ - медиана $$\Rightarrow$$ $$KL_{1}\cap SQ=H$$; $$\frac{SH}{HQ}=\frac{2}{1}$$, но $$\frac{SO}{OQ}=\frac{1}{1}$$ $$\Rightarrow$$ $$OH=\frac{2}{3}SQ-\frac{1}{2}SQ=\frac{1}{6}SQ$$, а $$HQ=\frac{1}{3}SQ$$ $$\Rightarrow$$ $$\frac{OH}{HQ}=\frac{1}{2}$$
Б) 1) Пусть $$N$$ - середина $$AB$$: в $$\bigtriangleup OQN$$ проведем $$HY\parallel QN$$. Через $$Y$$ построим $$BY\cap AO=R$$; из $$R$$ проведем $$RZ\parallel BC$$ $$\Rightarrow$$ $$(BRZC)$$ - сечение.
2) Пусть $$BR\cap CZ=L_{1}$$; $$LO\cap KL_{1}=I$$
3) $$\bigtriangleup L_{1}OI\sim\bigtriangleup LIK$$ $$\Rightarrow$$ $$\frac{L_{1}O}{LK}=\frac{L_{1}I}{IK}=\frac{1}{4}$$ $$\Rightarrow$$ $$L_{1}I=\frac{1}{5}L_{1}K$$ $$\Rightarrow$$ $$S_{L_{1}RZ}=\frac{1}{25}S_{L_{1}BC}$$ $$\Rightarrow$$ $$S_{RZCB}=\frac{24}{25}S_{L_{1}BC}$$
4) Пусть $$L_{2}$$ - проекция $$L_{1}$$ на $$(ABCD)$$ $$\Rightarrow$$ $$S_{L_{1}BC}=\frac{S_{L_{2}BC}}{\cos\angle L_{1}KL}(*)$$
5) $$S_{L_{2}BC}=\frac{1}{2}\cdot\frac{L_{2}K}{LK}S_{ABCD}=\frac{1}{2}\cdot\frac{3}{4}\cdot25=\frac{75}{8}$$
$$\angle SKL=60^{\circ}$$,т.к. $$SL=SK$$, а $$\angle SLK=60^{\circ}$$ $$\Rightarrow$$ $$\angle L_{1}KL=30^{\circ}$$. С учетом $$(*)$$: $$S_{L_{1}BC}=\frac{75}{8}\cdot\frac{2}{\sqrt{3}}=\frac{25\sqrt{3}}{4}$$ $$\Rightarrow$$ $$S_{RZCB}=\frac{25\sqrt{3}}{4}\cdot\frac{24}{25}=6\sqrt{3}$$