ЕГЭ Профиль
Задание 6135
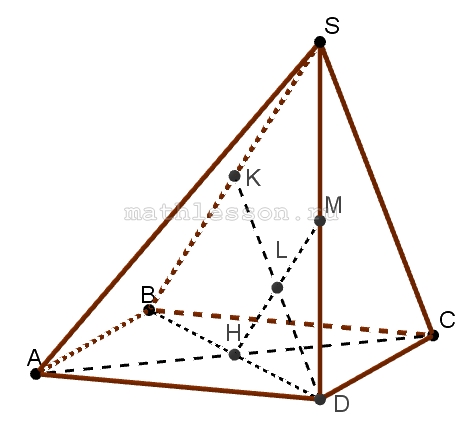
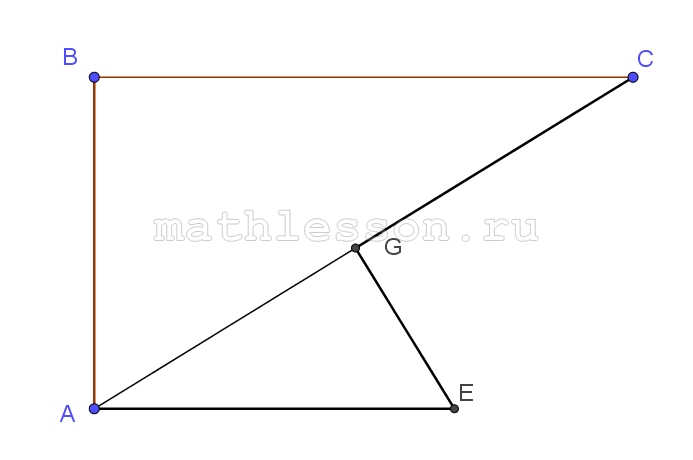
В основании пирамиды SABCD лежит квадрат ABCD со стороной 8. Боковое ребро SD перпендикулярно плоскости основания. Точка М‐середина высоты пирамиды. Плоскость ACM составляет угол 45 с плоскостью основания.
$$\angle MHD=45;SD\perp (ABC)$$
a)$$1)SD\perp (ABC)\Rightarrow SD$$-высота, тогда SM=MD.
2)ABCD-квадрат $$\Rightarrow AC\perp BD$$.
Пусть $$AC\cap BD=H$$,тогда $$DH\perp AC\Rightarrow MH\perp AC$$( по теореме о 3х перпендикулярах), тогда $$\angle MHD=45$$.
3)DH=HB(свойство диагоналей квдрата), тогда $$\Delta MHD\sim \Delta BSD\Rightarrow MH || SB\Rightarrow SB\left | \right |(AMC)$$.
б) 1)т.к. $$SB\left | \right | (AMC)$$,то d-расстояние от B до (AMC) равно расстоянию от SB до MH.
2) Опустим $$DK\perp SB, DK\cap MH=L\Rightarrow d=KL=\frac{1}{2}DK$$
3)из $$\Delta ABD: BD=\sqrt{8^{2}+8^{2}}=8\sqrt{2}$$.
4) $$\angle MHD=45\Rightarrow \Delta MHD$$ и $$\Delta BSD$$-равнобедренный $$\Rightarrow KD=BD*\sin B=8\sqrt{2}*\frac{\sqrt{2}}{2}=8$$.
5) $$KL=\frac{1}{2}KD=4.$$
Задание 6278
Сторона основания ABCD правильной пирамиды SABCD равна 2, угол между боковым ребром и основанием равен $$arccos \frac{1}{\sqrt{5}}$$ . На ребрах Sa и SD расположены точки Е и F так, что АЕ=2ES, DF=8SF. Через точки Е и F проведена плоскость $$\alpha$$ , параллельная АВ.
A) 1) $$\Delta DCA: CA=\sqrt{2^{2}+2^{2}}=2\sqrt{2}\Rightarrow$$ (теорема Пифагора). Тогда $$OA =\frac{CA}{2}=\sqrt{2}$$
2) $$\Delta SOA: \cos SAO=\frac{1}{\sqrt{5}}\Rightarrow$$. Тогда по основному тригонометрическому тождеству $$\sin SAO =\sqrt{1-\frac{1}{5}}=\frac{2}{\sqrt{5}}\Rightarrow$$ $$tg SAO=\frac{2}{\sqrt{5}}:\frac{1}{\sqrt{5}}=2$$. $$\frac{SO}{OA}=tg SAO\Rightarrow SO=OA*tg SAO=2\sqrt{2}$$
3) $$\Delta SON: SN=\sqrt{SO^{2}+ON^{2}}=\sqrt{1+8}=3$$ (по теореме Пифаогора). По условию: $$SH=\frac{1}{3}SN=1$$; $$SL=\frac{1}{9}SN=\frac{1}{3}$$. Из подобия треугольников: $$HH_{1}=\frac{1}{3}AD=\frac{2}{3}$$, $$H_{1}L=1-\frac{1}{3}=\frac{2}{3}$$
4) $$\Delta SNN_{1}: \cos S=\frac{1^{2}+1^{2}-(\frac{2}{3})^{2}}{2*1*1}=$$$$\frac{2-\frac{4}{9}}{2}=\frac{14}{2*9}=\frac{7}{9}$$ (из теоремы косинусов). $$LN=\sqrt{\frac{1}{3}^{2}+1^{2}-2*\frac{1}{3}*1*\frac{7}{9}}=$$$$\sqrt{\frac{10}{9}-\frac{14}{27}}=\sqrt{\frac{16}{27}}=\frac{4}{3\sqrt{3}}$$ (из теоремы косинусов). $$\cos LHH_{1}=\frac{\frac{16}{27}+(\frac{2}{3})^{2}-(\frac{2}{3})^{2}}{2*\frac{2}{3}*\frac{4}{3\sqrt{3}}}=$$$$\frac{16}{27}:\frac{16}{9\sqrt{3}}=\frac{9\sqrt{3}}{27}=\frac{\sqrt{3}}{3}\Rightarrow$$ $$LHH_{1}=\frac{\sqrt{6}}{3}$$ (из теоремы косинусов)
Б) 1)$$ZH=\frac{1}{3}ON=\frac{1}{3}$$. Из $$\Delta RZH: RZ=ZH *tg LHH_{1}=$$$$\frac{1}{3}\sqrt{2}=\frac{\sqrt{2}}{3}$$. $$ZO =\frac{2}{3}SO=\frac{2*2\sqrt{3}}{3}=\frac{4\sqrt{2}}{3}$$. $$RO=ZO+RZ=\frac{5\sqrt{2}}{3}$$
2) Из $$\Delta ROW: OW =\frac{RO}{tg LHH_{1}}=$$$$\frac{\frac{5 \sqrt{2}}{3}}{\sqrt{2}}=\frac{5}{3}$$
3) $$NW=OW-ON=\frac{5}{3}-1=\frac{2}{3}$$
4) $$NO=NW*\sin LHH_{1}=$$$$\frac{2}{3}*\frac{\sqrt{6}}{3}=\frac{2\sqrt{6}}{9}$$
Задание 6475
На ребрах NN1 и KN куба KLMNK1L1M1N1 отмечены такие точки P и Q, что $$\frac{KQ}{QN}=\frac{1}{4}$$, $$\frac{NP}{PN_{1}}=4$$&. Через точки M1,P,Q проведена плоскость. 1
А) Пусть KQ=t и QN=4t . Поскольку $$NN_{1}=KN$$, то $$PN=QN=4t$$ и $$N_{1}P=KQ=t$$.
Построим сечение плоскостью $$M_{1}PQ$$. Соединим отрезки $$QP, PM_{1}$$. Через точку $$M_{1}$$ проводим прямую $$M_{1}R\left |\right |PQ$$. Поскольку $$\Delta QPN\sim \Delta M_{1}RM$$, $$\frac{QN}{MR}=\frac{PN}{M_{1}M}=\frac{4}{5}\Rightarrow$$ $$MR=ML=5t$$, тогда точки R и L совпадают . Соединим точки L,Q и получаем сечение плоскостью - четырехугольник $$M_{1}LQP$$. Проведём $$M_{1}P LQ\cap M_{1}P=T$$. $$\Delta MTL\sim \Delta NQT$$, откуда $$\frac{ML}{QN}=\frac{MT}{NT}\Rightarrow$$ $$\frac{MN}{NT}=\frac{1}{4}$$ и $$NT=20t$$.
$$V_{LQNPM_{1}M}=V_{M_{1}LMT}-V_{PNQT}=$$$$\frac{1}{3}S_{MLT}*MM_{1}*PN=$$$$\frac{1}{3}*\frac{1}{2}*5t*25t*5t-\frac{1}{3}*\frac{1}{2}*4t*20t*4t=$$$$\frac{1}{6}(625t^{3}-320t^{3})=$$$$\frac{305}{6}t^{3}$$
$$V_{ost}=V_{KLMNK_{1}L_{1}M_{1}N_{1}}-V_{LQNPM_{1}M}=$$$$125t^{3}-\frac{305}{6}t^{3}=$$$$\frac{750t^{3}-305t^{3}}{6}=$$$$\frac{445}{6}t^{3}$$ и $$\frac{V_{LQNPM_{1}M}}{V_{ost}}=$$$$\frac{305}{405}=\frac{61}{89}$$
Б) Введем систему координат XYZ с центром в точке K(0;0;0), тогда соответственно Q(t;0;0),L(0;5t;0),P(5t;0;4t).
Составляем уравнение плоскости: $$ax+by+cz+d=0$$
$$\left\{\begin{matrix}at+d=0\\5bt+d=0\\5at+4ct+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a=-\frac{d}{t}\\b=-\frac{d}{5t}\\4ct=-5at-d\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a=-\frac{d}{t}\\b=-\frac{d}{5t}\\c=\frac{d}{t}\end{matrix}\right.$$ , тогда уравнение плоскости примет вид :
$$-\frac{d}{t}x-\frac{d}{5t}y+\frac{d}{t}z+d=0\Leftrightarrow$$ $$5x+y-5z=0$$ , вектор нормали $$\bar{n}(5,1,-5)$$. Применяем формулу расстояния от точки $$(x_{0}, y_{0},z_{0})$$ до плоскости $$ax+by+cz+d=0$$
$$p=\frac{\left | ax_{0}+by_{0}+cz_{0}+d \right |}{\sqrt{a^{2}+b^{2}+C^{2}}}$$, откуда $$p=\frac{\left | 5*0-1*0-5*0-5r \right |}{\sqrt{5^{2}+1^{2}+5^{2}}}=\frac{5t}{\sqrt{51}}$$. Поскольку ребро куба равно 3,т.е. 5t=3, тогда искомое расстояние $$p=\frac{3}{\sqrt{51}}$$
Ответ: $$p=\frac{3}{\sqrt{51}}$$
Задание 6664
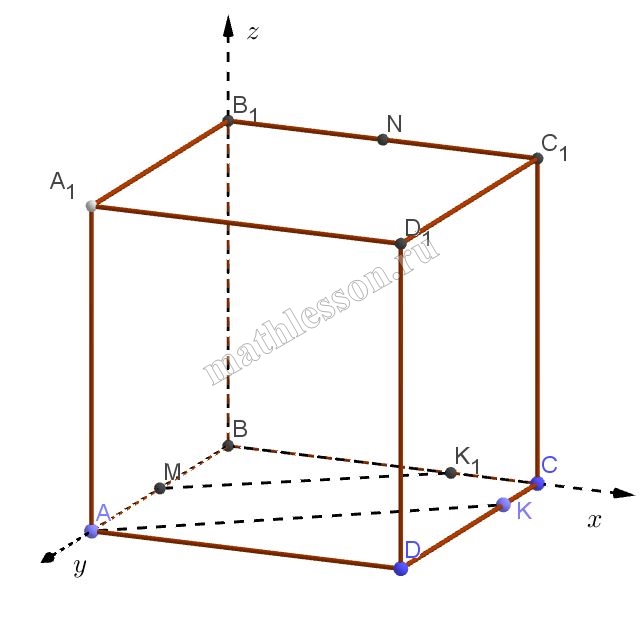
В кубе ABCDA1B1C1D1, ребро которого равно 6, точки М и N – середины ребер АВ и В1С1 соответственно, а точка К расположена на ребре DC так, что DK=2KC.
A) 1) Введем ортогольную систему координат , как показано на рисунке. Найдем координаты : M,N,A,K.
$$M(0;\frac{1}{2}A;0)\Rightarrow$$ $$M(0;3;0)$$
$$N(\frac{1}{2}B_{1}C_{1}; 0;BB_{1})\Rightarrow$$ $$N(3;0;6)$$
$$K(BC;\frac{1}{3}CD; 0)\Rightarrow$$ $$K(6;2;0)$$
$$A(0;AB;0)\Rightarrow$$ $$A(0;6;0)$$
2) Построим $$MK_{1}\left | \right |AK$$ : $$\Delta M_{1}BK_{1}\sim \Delta AKD$$ и $$\frac{M_{1}B}{KD}=\frac{BK_{1}}{AD}\Rightarrow$$ $$BK_{1}=\frac{3*6}{4}=4,5$$
Тогда : $$K_{1}(4,5 , 0,0)$$
3) Расстояние между MN и AK равно расстоянию от A до ($$MNK_{1}$$). Зададим уравнение ($$MNK_{1}$$):
$$\left\{\begin{matrix}a*0+b*3+c*0+d=0\\a*3+b*0+c*6+d=0\\a*4,5+b*0+c*0+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a=-\frac{2d}{9}\\b=-\frac{d}{3}\\c=-\frac{d}{8}\end{matrix}\right.$$
($$MNK_{1}$$) : $$-\frac{2}{9}x-\frac{1}{3}y-\frac{1}{18}z+1=0$$
Тогда расстояние: $$r=\frac{\left | -\frac{2}{9}*0-\frac{1}{43*6}-\frac{1}{18*0}+1 \right |}{\sqrt{(-\frac{2}{9})^{2}+(-\frac{1}{3})^{2}+(-\frac{1}{18})^{2}}}=$$$$\frac{1}{\frac{\sqrt{55}}{18}}=\frac{18}{\sqrt{53}}$$
Б) 1)Зададим уравнение (MNK):
$$\left\{\begin{matrix}a*0+b*3+c*0+d=0\\a*3+b*0+c*6+d=0\\a*6+B*2+c*0+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a=-\frac{d}{8}\\b=-\frac{d}{3}\\c=-\frac{5d}{36}\end{matrix}\right.$$
(MNK) : $$-\frac{1}{18}x-\frac{1}{3}y-\frac{5}{36}z+1=0$$
2) Найдем координаты $$A_{1}(0;6;6)$$. Тогда расстояние от $$A_{1}$$ до (MNK): $$\frac{\left | -\frac{1}{18}*0-\frac{1}{3}*6-\frac{5}{36}*6+1 \right |}{\sqrt{(-\frac{1}{18}^{2})+(-\frac{1}{3})^{2}+(-\frac{5}{36})^{2}}}=$$$$\frac{11}{6}*\frac{36}{\sqrt{173}}=\frac{66}{\sqrt{173}}$$
Задание 6758
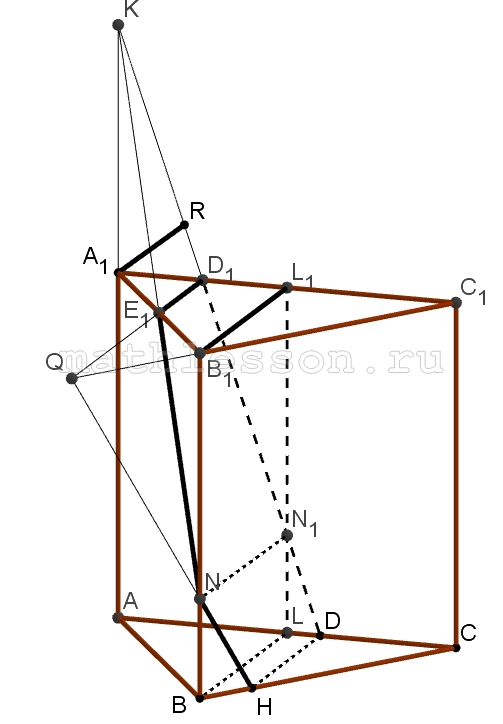
Основание прямой призмы ABCA1B1C1 равнобедренный треугольник ABC, в котором AB=BC=5, AC=6 . Высота призмы равна $$\sqrt{6}$$ . На сторонах A1C1, A1B1 и AC выбраны соответственно точки D1, E1 и D так, что , $$A_{1}D_{1}=\frac{A_{1}C_{1}}{4}$$, $$A_{1}E_{1}=B_{1}E_{1}$$, $$CD=\frac{AC}{3}$$, и через эти точки проведена плоскость.
А) 1) Соединим $$D_{1}E_{1}$$, т.к. $$(ABC) \left | \right |(A_{1}B_{1}C_{1})$$, то из D пойдет прямая DH ($$DH\cap BC=H$$) и $$D_{1}C_{1}\left | \right |DH$$
2) Пусть $$D_{1}E_{1}\cap C_{1}B_{1}=Q$$. Соединим $$QH\cap BB_{1}=N$$, соединим $$DD_{1}\Rightarrow$$ $$D_{1}D+NE_{1}$$ - искомое сечение
3) $$A_{1}D_{1}=D_{1}L_{1}$$($$B_{1}L_{1}$$ - высота ), $$A_{1}E_{1}=E_{1}B_{1}$$$$\Rightarrow$$ $$D_{1}E_{1}=\frac{1}{2}B_{1}L_{1}$$ и $$D_{1}E_{1}\left | \right |B_{1}L_{1}$$; $$B_{1}L_{1}=\sqrt{B_{1}C_{1}^{2}-L_{1}C_{1}^{2}}=4$$$$\Rightarrow$$ $$E_{1}D_{1}=2$$
4) $$DH\left | \right |D_{1}E_{1}\Rightarrow$$ $$DH\left | \right |BL$$ (BL - высота) $$\Rightarrow$$ $$\frac{DH}{LB}=\frac{CD}{CL}$$; $$CD=\frac{AC}{3}=2$$, $$CL=3\Rightarrow$$ $$DH=\frac{2*4}{3}=\frac{8}{3}$$
5) $$S_{D_{1}N_{1}NE_{1}}=\frac{D_{1}E_{1}*N_{1}N}{2}*DN_{1}$$; $$S_{NN_{1}DH}=\frac{DH*NN_{1}}{2}*DN_{1}$$ ($$AA_{1}\perp DH$$, $$AD\perp DH$$$$\Rightarrow$$ $$D_{1}D\perp DH$$); $$NK_{1}=BL=4;D_{1}B_{1}=\sqrt{D_{1}L_{1}^{2}+L_{1}N_{1}^{2}}$$$ $$D_{1}L=1,5 ; LD=1$$$$\Rightarrow$$ $$\frac{L_{1}N_{1}}{M_{1}L}=\frac{3}{2}$$ ($$\Delta D_{1}L_{1}N_{1}\sim \Delta N_{1}LD)$$$$\Rightarrow$$ $$L_{1}L=AA_{1}=\sqrt{6}=5x$$$$\Rightarrow$$ $$x=\frac{\sqrt{6}}{5}\Rightarrow$$ $$L_{1}N_{1}=\frac{3\sqrt{6}}{5}$$, $$N_{1}L=\frac{2\sqrt{6}}{5}$$)
$$D_{1}B_{1}=\sqrt{(\frac{3}{2})^{2}+(\frac{3\sqrt{6}}{5})^{2}}=\frac{21}{10}$$
$$D{1}D=\frac{7}{2}$$
$$DN_{1}=\sqrt{1^{2}+(\frac{2\sqrt{6}}{5})^{2}}=\frac{7}{5}$$
$$S_{D_{1}N_{1}NE_{1}}=\frac{2+4}{2}*\frac{21}{10}=\frac{63}{10}$$
$$S=\frac{63}{10}+\frac{14}{3}=\frac{329}{30}$$
$$S_{DHN_{1}N}=\frac{\frac{8}{3}+4}{2}*\frac{7}{5}=\frac{14}{3}$$
Б) 1) Пусть $$DD_{1}\cap AA_{1}=K$$ $$\Delta KD_{1}A_{1}\sim \Delta KAD$$; $$\frac{A_{1}D}{AD}=\frac{KD_{1}}{KD}=\frac{KA_{1}}{KA}=\frac{1,5}{4}=\frac{3}{8}$$. Пусть $$KA_{1}=x\Rightarrow$$ $$KA=x+\sqrt{6}\Rightarrow$$ $$\frac{x}{x+\sqrt{6}}=\frac{3}{8}\Leftrightarrow$$ $$8x=3x+3\sqrt{6}\Leftrightarrow$$ $$x=\frac{3\sqrt{6}}{5}$$. Пусть $$KD_{1}=y\Rightarrow$$ $$KD=y+\frac{7}{2}\Rightarrow$$ $$\frac{y}{y+\frac{7}{2}}=\frac{3}{8}\Rightarrow$$ $$y=\frac{21}{10}$$
2) Пусть $$A_{1}R\perp KD_{1}$$, но $$A_{1}D_{1}D_{1}E_{1}$$$$\Rightarrow$$ $$A_{1}R\perp D_{1}E_{1}$$ и $$A_{1}R\perp KD_{1}E_{1}$$.
$$A_{1}R=\frac{A_{1}K*A_{1}D_{1}}{KD_{1}}=$$$$\frac{\frac{3\sqrt{6}}{5}*\frac{3}{2}}{\frac{21}{10}}=$$$$\frac{9\sqrt{6}*10}{5*2*21}=\frac{3\sqrt{6}}{7}$$
Задание 6924
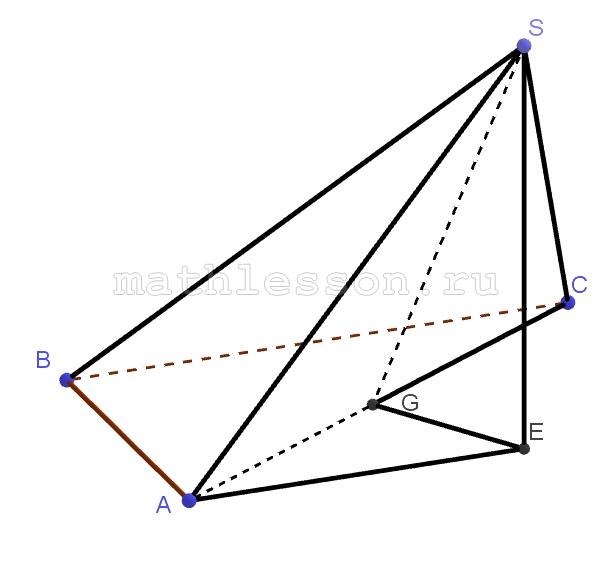
В треугольной пирамиде SABC плоские углы АВС и SAB прямые, двугранный угол между плоскостями ABS и АВС равен $$arcctg(\frac{2\sqrt{10}}{3})$$ . BC=7, AB=4
A) 1) Пусть $$SE \perp (ABC)$$, т.к. $$SA\perp AB$$, то по теореме о трех перпендикулярах : $$AE\perp AB\Rightarrow$$ $$ctg \angle SAE=\frac{2\sqrt{10}}{3}$$. Пусть $$EG\perp AC\Rightarrow$$ $$SG\perp AC$$ (по теореме о 3-x перпендикулярах )$$\Rightarrow$$ $$\angle SGE$$ - искомый
2) $$ctg ^{2}\angle SAE+1=\frac{1}{\sin ^{2}\angle SAE}$$$$\Rightarrow$$ $$\sin \angle SAE=\frac{3}{7}$$. Пусть SE=3x, тогда AS=7x; из $$\Delta ASE$$: $$AE=\sqrt{AS^{2}-SE^{2}}=\sqrt{40}x$$
3) $$\Delta ABC \sim \Delta AGE$$$$\Rightarrow$$ $$\frac{GE}{AB}=\frac{AE}{AC}=\frac{AG}{BC}(1)$$
Из $$\Delta ABC$$: $$AC=\sqrt{AB^{2}+AC^{2}}=\sqrt{65}$$
Из (1): $$AG=\frac{AE*BC}{AC}=\frac{7\sqrt{40}x}{\sqrt{65}}$$; $$GE=\frac{AE*AB}{AC}=\frac{4\sqrt{40}x}{\sqrt{65}}=\frac{8\sqrt{10}x}{\sqrt{65}}$$
4) из $$\Delta ASG$$: $$SG=\sqrt{AS^{2}-AG^{2}}=\frac{35 x}{\sqrt{65}}$$
5) $$\cos \angle SGE=\frac{GE}{SG}=\frac{8\sqrt{10}}{35}$$
Б) Пусть h-высота из B к (ASC) , тогда : $$V_{ABCS}=\frac{1}{3} S_{ASC}*h=\frac{1}{3}*S_{ABC}*SE$$$$\Leftrightarrow$$ $$h=\frac{S_{ABC}*SE}{S_{ASC}}=\frac{\frac{1}{2} *AB*BC*SE}{\frac{1}{2}*SG*AC}=$$$$\frac{AB*BC*SE}{SG*AC}=\frac{4*7*3x}{\frac{35x}{\sqrt{65}}*\sqrt{65}}=\frac{12}{5}$$
Задание 7039
Основанием пирамиды SABC является правильный треугольник, длина стороны которого равна $$\sqrt{3}$$. Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника АВС. Расстояние от точки О до стороны АС равно 1. Синус угла ОВА относится к синусу угла ОВС как 2:1. Площадь грани SAB равна $$\sqrt{\frac{5}{6}}$$.
A) 1) Пусть $$OL \perp CB$$; $$OM\perp AB$$; $$OK\perp AC$$ .
Из $$\Delta MOB$$: $$\sin \angle OBA=\frac{OM}{OB}$$
Из $$\Delta OLB$$: $$\sin \angle OBL =\frac{OL}{OB}$$
По условию $$\frac{\sin \angle OBA}{\sin \angle OBL}=2\Rightarrow$$ $$OM=2OL$$. Пусть $$OM=2x\Rightarrow$$ $$OL=x$$
2) $$S_{ABC}=S_{AOB}+S_{AOC}+S_{COB}\Leftrightarrow$$ $$\frac{1}{2} AC^{2} \sin 60=\frac{1}{2} AB(OM+OL+OK)\Leftrightarrow$$ $$\sqrt{3} \frac{\sqrt{3}}{2}=1+x+2x\Leftrightarrow$$ $$3x=\frac{1}{2}\Leftrightarrow$$ $$x=\frac{1}{6}\Rightarrow$$ $$OM=\frac{1}{3}; OL=\frac{1}{6}$$
3) $$S_{ABS}=\frac{\sqrt{5}}{\sqrt{6}}=\frac{1}{2}AB*SM$$ ($$OM\perp AB$$; $$SO\perp (ABC)$$$$\Rightarrow$$ $$AM\perp AB$$), тогда : $$SM=\frac{\sqrt{5}}{\sqrt{6}}*\frac{2}{1}*\frac{1}{\sqrt{3}}=\frac{\sqrt{10}}{3}$$
4) из $$\Delta MOS$$: $$SO=\sqrt{SM^{2}-OM^{2}}=1$$
5) $$V_{ABC}=\frac{1}{3} S_{ABC}*SO=$$$$\frac{1}{3}*\frac{3\sqrt{3}}{4}*1=\frac{\sqrt{3}}{4}$$
Б) 1) Аналогично (3): $$SL\perp CB$$. Пусть $$ON\perp SL\Rightarrow$$ $$ON$$ – расстояние от O до (SBC). Пусть $$AL_{1}\left | \right |AL$$ и $$AN_{1}$$ - расстояние от A до (SBC) , тогда $$\Delta AL_{1}N_{1}\sim \Delta OLN$$ и $$\frac{AN_{1}}{ON}=\frac{AL_{1}}{OL}$$
2) из $$\Delta OSL$$: $$SL=\sqrt{OS^{2}+OL^{2}}=\frac{\sqrt{37}}{6}$$; $$ON=\frac{OS*OL}{SL}=\frac{1}{\sqrt{37}}$$
3) из $$\Delta ABC$$ : $$AL_{1} =AB \sin 60=\frac{3}{2}\Rightarrow$$ $$AN_{1} :\frac{1}{\sqrt{37}}=\frac{3}{2}:\frac{1}{6}\Rightarrow$$ $$AN_{1}=\frac{9}{\sqrt{37}}$$
Задание 7200
Длина ребра куба ABCDA1B1C1D1 равна 1. На ребре АА1 взята точка Е так, что длина отрезка АЕ равна 1/3. На ребре ВС взята точка F так, что длина отрезка BF равна 1/4. Через центр куба и точки Е и F проведена плоскость $$\alpha$$.
A) 1) Пусть $$A_{1}C\cap B_{1}D=M\Rightarrow$$ M –центр куба; через E и M проведем прямую (они лежат в плоскости ($$AA_{1}C$$) )$$\cap CC_{1}=I$$
2) $$I$$ и $$F \in (BB_{1}C_{1})\Rightarrow$$ проведем прямую; $$IF\cap BB_{1}=K$$; $$E$$ и $$K \in (BB_{1}A_{1})\Rightarrow$$ соединяем , $$EK\cap AB=J$$; $$F$$ и $$J \in (ABC)\Rightarrow$$ соединяем .
3) $$(BB_{1}C_{1}) \left | \right |(AA_{1}D_{1})\Rightarrow$$ из E прямую, параллельную IF; она $$\cap A_{1}D_{1} =G$$. Аналогично из G прямую параллельную $$JF\Rightarrow \cap C_{1}D_{1}=H$$; соединим H и I $$\Rightarrow$$ (EGHIFJ)-искомое сечение ($$\alpha$$)
4) Введем отртогональную систему координат как показано на рисунке и зададим уравнение $$(\alpha )$$: $$E(0;0;\frac{1}{3})$$;
$$F(1; \frac{1}{4} ;0)$$; $$M(\frac{1}{2}; \frac{1}{2}; \frac{1}{2})$$. Пусть $$ax+by+cz+d=0$$ уравнение ($$\alpha$$), тогда:
$$\left\{\begin{matrix}a*0+b*0+c*\frac{1}{3}+d=0 & & & \\a*1+b*\frac{1}{4}+c*0+d=0\\a*\frac{1}{2}+\frac{1}{2}b+\frac{1}{2}c+d=0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}c=-3d\\4a+b+4d=0\\a+b+c+2d=0\end{matrix}\right.$$
Подставим из первого в третье: $$a+b-3d+2d=0\Rightarrow$$ $$a+b-d=0\Rightarrow$$ $$a=d-b$$
Подставим во второе: $$4d-4b+b+4d=0\Rightarrow$$ $$-3b=-8d\Rightarrow$$ $$b=\frac{8d}{3}\Rightarrow$$ $$a=-\frac{5d}{3}$$
Тогда уравнение плоскости $$(\alpha)$$: $$\frac{-5d}{3}x+\frac{8d}{3}y-3dz+d=0$$ $$\Rightarrow$$ $$-5x+8y-9z+3=0\Rightarrow$$ нормаль вектора для (EGH): $$\bar{n}(-5 ;8; -9)$$. Для (ABC): $$\bar{AA_{1}}(0; 0; 1)$$ (ось Oz)
Тогда $$\cos (\alpha ; (ABC))=\cos (\bar{n}$$; $$\bar{AA_{1}})=\frac{\left | -5*0+8*0-9*1 \right |}{\sqrt{(-5)^{2}+8^{2}+(-9)^{2}}*\sqrt{0^{2}+0^{2}+1^{1}}}=$$$$\frac{9}{\sqrt{170}}\Rightarrow$$ угол между $$\alpha$$ и (ABC) : $$\arccos \frac{9}{\sqrt{170}}$$
Б) Найдем расстояние от $$B_{1}(1; 0; 1)$$ до $$\alpha$$: $$r=\frac{\left | -5*1+8*0+(-9)*1+3 \right |}{\sqrt{(-5)^{2}+8^{2}+(-9)^{2}}}=\frac{11}{\sqrt{170}}$$
Задание 7683
В прямоугольном параллелепипеде ABCDA1B1C1D1 проведена секущая плоскость, содержащая диагональ АС1 и пересекающая ребра ВВ1 и DD1 в точках F и E соответственно. Известно, что AFC1E – ромб и АВ=3, ВС=2, АА1=5
Задание 7782
В правильной треугольной пирамиде ABCD угол ADC равен $$2arcsin\frac{1}{6}$$ , а сторона основания АВС равна 2. Точки K, M, N – середины ребер АВ, CD и АС соответственно. Точка Е лежит на отрезке КМ и 3ME=KE . Через точку Е проходит плоскость $$\alpha$$ перпендикулярно отрезку КМ.
Задание 8268
В правильной шестиугольной пирамиде SABCDEF сторона основания АВ=1, высота SO=2, точка М‐середина ребра BS.
А) 1) По свойству правильного шестиугольника: $$AF\parallel BE$$; $$AF=\frac{BE}{2}$$
2) Из $$\bigtriangleup BSE$$: $$MN$$ - средняя линия $$\Rightarrow$$ $$MN\parallel BE$$; $$MN=\frac{BE}{2}$$ $$\Rightarrow$$ $$AF=MN$$; $$AF\parallel MN$$ $$\Rightarrow$$ $$AFNM$$ - параллелограм $$\Rightarrow$$ $$AM\parallel FN$$
Б) 1) Пусть $$MM'\perp BE$$ $$\Rightarrow$$ из $$\bigtriangleup BMM'$$: $$BM=\frac{BO}{2}$$ $$\Rightarrow$$ $$M'E=\frac{3}{2}$$; $$MM'=\frac{SO}{2}=1$$ $$\Rightarrow$$ По т. Пифагора: $$ME=\sqrt{M'E^{2}-M'M^{2}}=\frac{\sqrt{13}}{2}$$
2) из $$\bigtriangleup AFE$$: $$AE=\sqrt{AF^{2}+FE^{2}-2AF\cdot FE\cos F}=\sqrt{1+1-2\cdot1\cdot1\cdot(-\frac{1}{2})}=\sqrt{3}$$
3) из $$\bigtriangleup AMM'$$: $$AM=\sqrt{M'A^{2}+M'M^{2}}$$; $$M'A=\frac{1}{2}AC=\frac{\sqrt{3}}{2}$$ $$\Rightarrow$$ $$AM=\sqrt{\frac{3}{4}+1}=\frac{\sqrt{7}}{2}$$
4) из $$\bigtriangleup AME$$: $$\cos M=\frac{AM^{2}+ME^{2}-AE^{2}}{2\cdot AM\cdot ME}=\frac{\frac{7}{4}+\frac{13}{4}-3}{2\cdot\frac{\sqrt{7}}{2}\cdot\frac{\sqrt{13}}{2}}=\frac{4}{\sqrt{13\cdot7}}$$ $$\Rightarrow$$ $$\sin M=\sqrt{1-\cos^{2}M}=\frac{5\sqrt{3}}{\sqrt{7\cdot13}}$$
5) Пусть $$EH\perp AM$$ $$\Rightarrow$$ $$EH=ME\cdot\sin M=\frac{\sqrt{13}}{2}\cdot\frac{5\sqrt{3}}{\sqrt{7\cdot13}}=2,5\sqrt{\frac{3}{7}}$$
Задание 8779
Задание 8798
Задание 9781
В основании четырехугольной пирамиды SKLMN лежит равнобедренная трапеция KLMN, описанная около окружности и такая, что KN=LM=4, MN>KL и угол между прямыми KN и LM равен 600. Две противоположные грани этой пирамиды перпендикулярны основанию и SM=12.