Тригонометрические уравнения

   А) $$4 \sin ^{3}x=3 \cos(x-\frac{\pi}{2})\Leftrightarrow$$$$4 \sin ^{3}x=3 \cos(\frac{\pi}{2}-x)\Leftrightarrow$$$$4 \sin^{3}x=3 \sin x\Leftrightarrow$$$$4 \sin^{3}x-3 \sin x=0\Leftrightarrow$$$$\sin x(4 \sin^{2}x-3)=0$$

$$\left[\begin{matrix}\sin x=0\\4 \sin^{2}x-3=0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\pi n,n \in Z\\\sin^{2}x=\frac{3}{4}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\pi n , n \in Z\\\sin x=\frac{\sqrt{3}}{2}\\\sin x=-\frac{\sqrt{3}}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x_{1}=\pi n, n\in Z\\x_{2}=(-1)^{n}\frac{\pi}{3}+\pi k, k \in Z\\x_{3}=(-1)^{m+1}+\pi m,m \in Z\end{matrix}\right.$$

   Б) $$x_{1}: 4\pi$$

$$x_{2}:4\pi+\frac{\pi}{3}=\frac{13\pi}{3}$$

$$x_{3}:4 \pi -\frac{\pi}{3}=\frac{11\pi}{3}$$

     А) $$tg^{2}x+(1+\sqrt{3})tgx+\sqrt{3}=0$$

$$D=(1+\sqrt{3})^{2}-4\sqrt{3}=1+2\sqrt{3}+3-4\sqrt{3}=1-2\sqrt{3}+3=(1-\sqrt{3})^{2}$$

$$\left[\begin{matrix}tg x=\frac{-1-\sqrt{3}+\sqrt{3}-1}{2}=-1\\tgx=\frac{-1-\sqrt{3}-\sqrt{3}+1}{2}=-\sqrt{3}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x_{1}=-\frac{\pi}{4}+\pi n , n \in Z\\x_{2}=-\frac{\pi}{3}+\pi k, k \in Z \end{matrix}\right.$$

   Б) $$x_{1}$$: $$3\pi -\frac{\pi}{4}=\frac{11\pi}{4};$$$$4\pi -\frac{\pi}{4}=\frac{15\pi}{4}$$

$$x_{2}$$:$$3\pi-\frac{\pi }{3}=\frac{\pi}{3};$$ $$4\pi-\frac{\pi}{3}=\frac{11\pi}{3}$$

   А) Так как слева модуль, то ОДЗ (D): $$\sin 2x\geq 0$$

Возведем обе части в квадрат:

$$(\left | \cos x+\sin x \right |)^{2}=(\sqrt{2}\sin 2x)^{2}$$

$$\cos^{2}x+2\sin x \cos x+\sin^{2}x=2 \sin ^{2}2x$$

$$1+\sin 2x -2 \sin^{2}x=0$$

$$D=1+8-9$$

$$\left\{\begin{matrix}\sin 2x =\frac{-1+3}{-4} =-\frac{1}{2}\sin 2x=\frac{-1-3}{-4}=1\end{matrix}\right.$$

$$\sin 2x=-\frac{1}{2} \notin D$$

$$\sin 2x=1\Leftrightarrow 2x=\frac{\pi}{2}+2 \pi k,k\in Z\Leftrightarrow$$$$x=\frac{\pi}{4}+\pi k,k \in Z$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

a) $$\cos x\cos\frac{\pi}{3}-\sin x\sin\frac{\pi}{3}+\sin x\cos\frac{\pi}{6}+\cos x\sin\frac{\pi}{6}-\cos2x=1$$; $$\frac{1}{2}\cos x-\frac{\sqrt{3}}{2}\sin x+\frac{\sqrt{3}}{2}\sin x+\frac{1}{2}\cos x -2\cos^{2}x+1-1=0$$; $$\cos x-2\cos^{2}x=0$$; $$\cos x(1-2\cos x)=0$$; $$\left\{\begin{matrix}\cos x=0\\\cos x=\frac{1}{2}\end{matrix}\right.$$ $$\Leftrightarrow$$; $$\left\{\begin{matrix}x=\frac{\pi}{2}+\pi n,n\in Z\\x=\pm\frac{\pi}{3}+2\pi k,k\in Z\end{matrix}\right.$$ 

б) Все 4 корня попадают $$-\frac{3\pi}{2};-\frac{\pi}{2};-\frac{\pi}{3}$$;$$\frac{\pi}{3};\frac{\pi}{2}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

a) $$4\cdot(\sin4x-\sin2x)=\sin x\cdot(4\cos^{2}3x+3)$$; $$8\sin\frac{4x-2x}{2}\cdot\cos\frac{4x+2x}{2}-\sin x(4\cos^{2}3x+3)=0$$; $$8\sin x\cdot\cos3x-\sin x(4\cos^{2}3x+3)=0$$; $$\sin x(8\cos3x-4\cos^{2}3x-3)=0$$; $$\left\{\begin{matrix}\sin x=0(1)\\4\cos^{2}3x-8\cos3x+3=0(2)\end{matrix}\right.$$

1) $$\sin x=0$$; $$x=\pi n,n\in Z$$

2) $$\cos3x=t$$; $$4t^{2}-8t+3=0$$; $$D=64-48=16$$; $$t_{1}=\frac{8+4}{4}=\frac{3}{2}$$; $$t_{2}=\frac{8-4}{4}=\frac{1}{2}$$;

$$\cos x=\frac{3}{2}$$ - решений нет ($$|\cos3x\leq1|)$$; $$\cos3x=\frac{1}{2}$$; $$3x=\pm\frac{\pi}{3}+2\pi k,k\in Z$$; $$x=\pm\frac{\pi}{9}+\frac{2\pi k}{3},k\in Z$$;

б) $$0\leq\pi n\leq\frac{3\pi}{2}$$; $$0\leq n\leq\frac{3}{2}$$ $$\Rightarrow$$ $$n=0;1$$

2) $$x=\pm\frac{\pi}{9}+\frac{2\pi k}{3},k\in Z$$; $$0\leq\frac{\pi}{9}+\frac{2\pi k}{3}\leq\frac{3\pi}{2}$$; $$-\frac{\pi}{9}\leq\frac{2\pi k}{3}\leq\frac{25\pi}{18}$$; $$-\frac{1}{6}\leq k\leq\frac{75}{36}$$; $$\Rightarrow$$ $$k=0;1;2$$

$$x=\frac{\pi}{9}+\frac{2\pi}{3}\cdot0=\frac{\pi}{9}$$; $$x=\frac{\pi}{9}+\frac{2\pi}{3}\cdot2=\frac{13\pi}{9}$$; $$x=\frac{\pi}{9}+\frac{2\pi}{3}\cdot1=\frac{7\pi}{9}$$; $$0\leq-\frac{\pi}{9}+\frac{2\pi k}{3}\leq\frac{3\pi}{2}$$; $$\frac{\pi}{9}\leq\frac{2\pi k}{3}\leq\frac{29\pi}{18}$$; $$\frac{1}{9}\leq k\leq\frac{87}{36}$$; $$\Rightarrow$$ $$k=1;2$$ $$\Rightarrow$$ $$x=-\frac{\pi}{9}+\frac{2\pi}{3}\cdot1=\frac{5\pi}{9}$$; $$x=-\frac{\pi}{9}+\frac{2\pi}{3}\cdot2=\frac{11\pi}{9}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     А)  Применим формулу косинуса двойного угла $$\cos 2x=1-2\sin^{2}x$$: $$\cos 2x+3\sqrt{2}\sin x-3=0\Leftrightarrow$$ $$1-2\sin^{2}x+3\sqrt{2}\sin x-3=0\Leftrightarrow$$ $$2\sin^{2}x-3\sqrt{2}+2=0$$

   $$D=(3\sqrt{2})^{2}-4*4=18-16=2$$

   Поскольку $$-1\leq \sin x\leq 1$$, то  $$\sin x=\frac{\sqrt{2}}{2}\Leftrightarrow$$ $$x=(-1)^{k}\frac{\pi}{4}+\pi k , k \in Z$$

   $$\left[\begin{matrix}\sin x=\frac{3\sqrt{2}+\sqrt{2}}4{=\sqrt{2}}\\\sin x=\frac{3\sqrt{2}-\sqrt{2}}{2}=\frac{\sqrt{2}}{2}\end{matrix}\right.$$

     Б) Найдем корни уравнения на промежутке  $$(\frac{\pi}{4};\pi]$$ с помощью тригонометрического круга : $$x=\frac{3\pi}{4}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

а)Воспользуемся формулами приведения: $$3\sin^{2} x -\cos (\frac{9\pi}{2}-x)\sin (\frac{3\pi}{2}+x) -2 =0\Leftrightarrow $$$$3\sin^{2} x +\sin x \cos x - 2(\sin^{2} x +\cos ^{2} x =0\Leftrightarrow $$$$\sin^{2} x +\sin x \cos x -2\cos^{2} x=0$$

Поделим обе части на $$\cos^{2} x \neq 0$$ и решим уравнение относительно $$tg x$$:

$$tg^{2} x +tg-2=0 \Leftrightarrow $$$$tgx=1 ; tgx=-2 \Leftrightarrow $$$$x=\frac{\pi}{4}+\pi*n ; x=-arctg2 +\pi*n , n \in Z$$

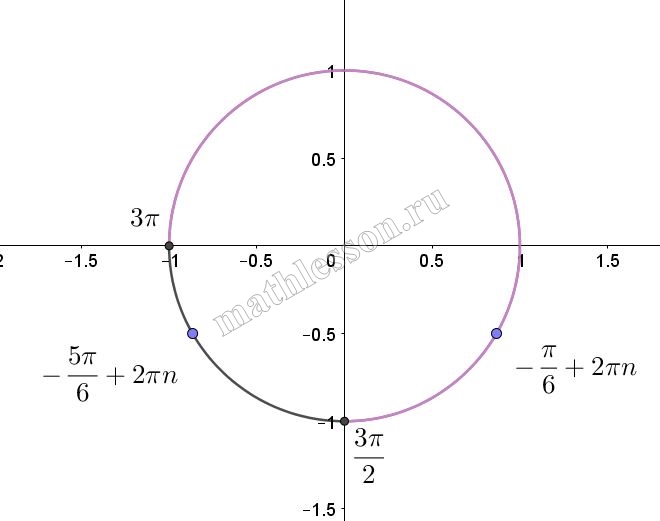
б)Отметим на единичной окружности полученные решения и отрезок. Полученные решения представим как $$x=\frac{\pi}{4}+\pi*n \Leftrightarrow x=\frac{\pi}{4}+2\pi*n ; x=-\frac{3\pi}{4}+\pi*n$$

$$ x=-arctg2 +\pi*n \Leftrightarrow x=-arctg2 +2\pi*n ; x=\pi-arctg2 +\pi*n$$

Как видим, попадает только два. Чтобы найти первый мы к $$3\pi$$ прибавляем $$\frac{\pi}{4}$$ и получаем $$\frac{13\pi}{4}$$. Чтобы найти второй мы из $$4\pi$$ вычитаем $$arctg2$$ и получаем $$4\pi - arctg2$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     А) Применим формулы привидения : $$\cos (5x-\frac{9\pi}{2})=\cos (\frac{\pi}{2}-5x)=\sin 5x$$, $$\sin (3x+\pi)=-\sin 3x$$

Уравнение имеет вид: $$\sin x+\sin 5x=-\sqrt{3}\sin 3x\Leftrightarrow$$ $$2\sin 3x \cos 2x +\sqrt{3}\sin 3x=0\Leftrightarrow$$ $$\sin 3x (2 \cos 2x+\sqrt{3})\Leftrightarrow$$ $$\left[\begin{matrix}\sin 3x=0\\2 \cos 2x+\sqrt{3}=0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\sin 3x=0\\\cos 2x=-\frac{\sqrt{3}}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}3x=\pi n, n \in Z\\2x=\pm \frac{5\pi}{6}+2\pi k , k \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi n}{3}, n \in Z\\x=\pm \frac{5\pi}{12}+\pi k , k \in Z\end{matrix}\right.$$

     Б) Отбор корней $$\in [\pi ;\frac{\pi}{2}]$$ проведем на тригонометрической окружности :

$$x_{1}=-\pi$$; $$x_{2}=-\pi+\frac{\pi}{3}=-\frac{2\pi}{3}$$; $$x_{3}=-\pi+\frac{5\pi}{12}=-\frac{7\pi}{12}$$; $$x_{4}=-\frac{5\pi}{12}$$; $$x_{5}=-\frac{\pi}{3}$$; $$x_{6}=0$$; $$x_{7}=\frac{\pi}{3}$$; $$x_{8}=\frac{5\pi}{12}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\cos \frac{\pi x}{6}=-0,5\Leftrightarrow$$ $$\frac{\pi x}{6}=\pm \frac{2 \pi}{3}+2 \pi n, n \in Z\Leftrightarrow$$ $$x=\pm 4+12n, n \in Z$$

Найдем наибольший отрицательный :

$$\left\{\begin{matrix}4+12n<0\\-4+12n<0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}12n<-4\\12<4\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}n<-\frac{1}{3}\\n<\frac{1}{3}\end{matrix}\right.\Leftrightarrow$$ $$\left{\begin{matrix}n=-1\\n=0 & &\end{matrix}\right.$$

$$x_{1}=4+12(-1)=-8$$, $$x_{2}=-4+12*0=-4$$

Наибольший отрицательный: -4.

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

A) $$\cos2x+\sqrt{2}\cos(x+\frac{5\pi}{4})=\sin x$$; $$\cos2x+\sqrt{2}(\cos x\cos\frac{5\pi}{4}-\sin x\sin\frac{5\pi}{4})-\sin x=0$$; $$\cos2x+\sqrt{2}\cos x\cdot(-\frac{\sqrt{2}}{2})-\sqrt{2}\sin x\cdot(-\frac{\sqrt{2}}{2})-\sin x=0$$; $$\cos2x-\cos x+\sin x-\sin x=0$$; $$2\cos^{2}x-1-\cos x=0$$; Пусть $$\cos x=y\in[-1;1]$$; $$2y^{2}-y-1=0$$; $$D=1+8=9$$; $$y_{1}=\frac{1+3}{4}=1$$; $$y_{2}=\frac{1-3}{4}=-\frac{1}{2}$$; $$\left\{\begin{matrix}\cos x=1\\\cos x=-\frac{1}{2}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=2\pi n,n\in Z\\x=\pm\frac{2\pi}{3}+2\pi k,k\in Z\end{matrix}\right.$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

   А) $$\frac{5}{\cos^{2}(\frac{13\pi}{2}-x)}+\frac{7}{\sin x}-6=0$$; $$\left\{\begin{matrix}\cos^{2}(\frac{13\pi}{2}-x)\neq0\\\sin x\neq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\sin^{2}x\neq0\\\sin x\neq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$x\neq\pi n,n\in Z$$

$$\frac{5}{\sin^{2}x}+\frac{7}{\sin x}-6=0$$

Замена: $$\frac{1}{\sin x}=y$$

$$5y^{2}+7y-6=0$$;

$$D=49+120=13^{2}$$;

$$y_{1}=\frac{-7+13}{10}=\frac{6}{10}$$; 

$$y_{2}=\frac{-7-13}{10}=-2$$

$$\left\{\begin{matrix}\frac{1}{\sin x}=-2\\\frac{1}{\sin x}=\frac{6}{10}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\sin x=-\frac{1}{2}\\\sin x=\frac{10}{6}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=(-1)^{n+1}\frac{\pi}{6}+\pi n,n\in Z\\ \varnothing \end{matrix}\right.$$

   Б)Построим единичную окружность, отметим полученные корни и заданный промежуток:

Как видим, на заданном промежутке есть только корень $$\frac{\pi}{6}+2\pi n$$. Найдем его значение: $$2\pi- \frac{\pi}{6}=\frac{11\pi}{6}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\sin 2x=\sin x -2\cos x +1 \Leftrightarrow$$$$2\sin x \cos x-\sin x +2\cos x -1=0 \Leftrightarrow$$$$2\cos x(\sin x+1)-1(\sin x +1)=0 \Leftrightarrow$$$$(\sin x+1)(2\cos x - 1 )=0 \Leftrightarrow$$$$ \left\{\begin{matrix} \sin x = -1\\ \cos x = \frac{1}{2}\end{matrix}\right.\Leftrightarrow $$$$ \left\{\begin{matrix}x=-\frac{\pi}{2}+2\pi n\\x=\pm \frac{\pi}{3}+2\pi k \end{matrix}\right.(n,k\in Z)$$

Отметим полученные корни на единичной окружности, выделим необходимый промежуток и найдем частные случаи полученных корней:

Получим: $$\frac{3\pi}{2} ; \frac{5\pi}{3} ; \frac{7\pi}{3}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

a)$$2*\sin*\left ( x+\frac{\pi }{3} \right )-\sqrt{3}*\cos 2x=\sin x+\sqrt{3};$$

$$2*\left ( \sin x*\cos \frac{\pi }{3}+\sin\frac{\pi }{3}*\cos x \right )-\sqrt{3}*\cos 2x-\sin x-\sqrt{3}=0;$$

$$2*\sin x*\frac{1}{2}+2*\frac{\sqrt{3}}{2}*\cos x-\sqrt{3}*\cos 2x-\sin x-\sqrt{3}=0$$

$$\sqrt{3}*\cos x-\sqrt{3}* \cos 2x-\sqrt{3}=0;$$

$$\cos x- \cos 2x-1=0\Leftrightarrow$$$$\cos x-(2\cos^{2} x-1)-1=0$$

$$\cos x-2* \cos ^{2}x=0$$

$$\cos x *\left ( 1-2*\cos x \right )=0$$

$$\left [ \begin{matrix}cos x=0 & & \\1-2*\cos x=0 & &\end{matrix}\right.\Leftrightarrow \left [ \begin{matrix}x=\frac{\pi }{2}+\pi* k,k\varepsilon Z & & \\x=\pm \frac{\pi }{3}+2*\pi *n.n\varepsilon Z & &\end{matrix}\right.$$

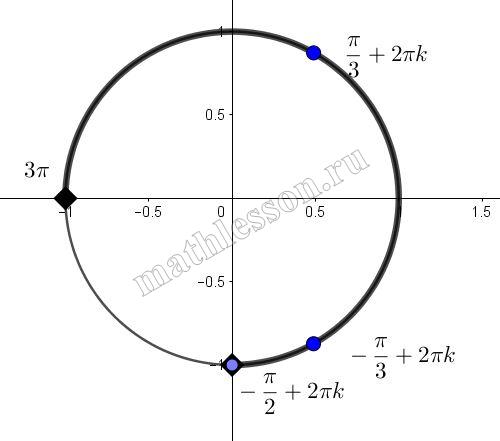
б)Найдем частные случаи корней, принадлежащие выбранному промежутку (синим цветом):

$$-2*\pi +\frac{\pi }{3}=-\frac{5*\pi }{3}$$

$$-2*\pi+\frac{\pi}{2}=-\frac{3*\pi}{2}$$

$$-\pi+\frac{\pi}{2}=-\frac{\pi}{2}$$