ЕГЭ (профиль) / (C6) Задача с параметром

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}(x^{2}+(y-7)^{2}-9)((x-4)^{2}+(y-3)^{2}-1)=0\\ax-y-4a-2=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x^{2}+(y-7)^{2}=9(*) & \\(x-4)^{2}+(y-3)^{2}=1(**) & \\y=a(x-4)-2\end{matrix}\right.$$

$$(*) x^{2}+(y-7)^{2}=9$$ - окружность с центром $$O_{1}(0;7)$$ и радиусом $$R=3$$

$$(**)(x-4)^{2}+(y-3)^{2}=1$$ – окружность с центром $$O_{2}(4,3)$$ и радиусом $$R=1$$

$$y=a(x-4)-2$$ - пучок прямых ,проходящих через точку $$A(4,-2)$$

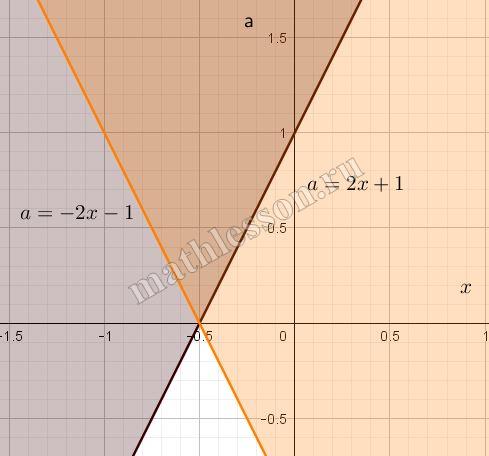
     Пусть $$B_{1}C$$ - точки касания прямой $$y=a(x-4)-2$$ с окружностью (**) с , а, $$D_{1}E$$ - с окружностью (*)

     Система будет иметь 4 решения , если прямая будет пересекать окружности в 4 точках. На рисунках слева оранжевым цветом выделены пограничные случаи расположения прямой в таком случае (4 решения от момента касания в точке D до момента касания в точке  C при повороте прямой против часовой стрелки ,не включая данные значения)

     Найдем соответствующие значения параметра a .Воспользуемся формулой нахождения расстояния от точки с координатами $$(x_{0},y_{0})$$ до прямой $$ax+by+c=0$$: $$p=\frac{\left | ax_{0}+by_{0}+c \right |}{\sqrt{a^{2}+b^{2}}}$$

     Расстояние от точки $$O_{1}$$ до прямой  $$y=a(x-4)-2$$ равно $$\frac{\left | -7-4a-2 \right |}{\sqrt{a^{2}+1}}=\frac{\sqrt{4a+9}}{\sqrt{a^{2}+1}}$$

     С другой стороны , расстояние от точки $$O_{1}$$ до прямой $$y=a(x-4)-2$$ равно радиусу окружности (*) , откуда $$\frac{\left | 4a+9 \right |}{\sqrt{a^{2}+1}}=3\Rightarrow$$ $$(4a+9)^{2}=9(a^{2}+1)\Leftrightarrow$$ $$16a^{2}+72a+81=9a^{2}+9\Leftrightarrow $$$$7a^{2}+72a+72=0\Leftrightarrow$$ $$\left[\begin{matrix}a=-\frac{36+6\sqrt{22}}{7}\\a=-\frac{36-6\sqrt{22}}{7}\end{matrix}\right.$$

     Поскольку касание происходит в точке D, то угловой коэффициент прямой в случае касания в точке D должен быть меньше, чем в случае касания в точке  E, поэтому  $$a=-\frac{36+6\sqrt{22}}{7}$$

    Аналогичным образом находим значения параметра в случае касания с окружностью (**):

$$\frac{\left | 4a-3-4a-2 \right |}{\sqrt{a^{2}+1}}=1\Leftrightarrow$$ $$\frac{5}{\sqrt{a^{2}+1}}=1\Leftrightarrow$$ $$25=a^{2}+1\Leftrightarrow$$ $$a^{2}=24\Leftrightarrow$$ $$\left[\begin{matrix}a=2\sqrt{6}\\a=-2\sqrt{6}\end{matrix}\right.$$

     Касание прямой с окружностью  в точке C соответствует значению $$a=-2\sqrt{6}(a=2\sqrt{6}$$ - касание в точке B). Окончательно получим , что система имеет 4 решения при $$a_{1,2}=-\frac{36+6\sqrt{22}}{7};-2\sqrt{6}.$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Используем «неравенство треугольника» :$$\left | x+y \right |\leq \left | x \right |+\left | y \right |$$, где равенство достигается , если x  и y или оба неотрицательны , или оба неположительны.

     Поскольку $$a^{2}-a*1>0$$, будем иметь: $$a^{2}-a*1=\left | a^{2}-a+1 \right |=$$$$\left | (a^{2}+3-x)+(x-a-2) \right |\leq$$ $$\left | a^{2}+3-x \right |+\left | x-a-2 \right |\leq$$ $$\left | a^{2}+3-x \right |+\left | x-a-2 \right |+\left | x-3a-1 \right |=$$$$a^{2}-a+1(1)$$

     Следовательно , в цепочке (1) все неравенства обращаются в равенства. Это возможно лишь в том случае , когда $$a^{2}+3-x$$ и $$x-a-2$$ неотрицательны ( так как их сумма положительна) , а $$x-3a-1=0$$. Получим систему условий: $$\left\{\begin{matrix}x-3a-1=0\\a^{2}+3-x\geq 0\\x-a-2\geq 0\end{matrix}\right.(2)$$

     Подставим значение  $$x=3a+1$$ из первого неравенства системы (2) во второе и третье:

$$\left\{\begin{matrix}a^{2}-3a+2\geq 0\\2a-1\geq 0\end{matrix}\right.\Rightarrow$$ $$\left\{\begin{matrix}x \in (-\infty; 1]\cup [2;+\infty )\\a\geq 0,5\end{matrix}\right.\Rightarrow$$ $$a\in [0,5; 1]\cup [2;+\infty )$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$(x^{2}-5+\ln(x+a))^{2}=(x^{2}-5)^{2}+\ln^{2}(x+a)$$

ОДЗ: $$x+a>0 \Leftrightarrow x>-a$$

$$(x^{2}-5)^{2}+2(x^{2}-5)\ln^{2}(x+a)=(x^{2}-5)^{2}+\ln^{2}(x-a)$$

$$(x^{2}-5)\ln(x-a)=0$$

$$\left\{\begin{matrix}x^{2}-5=0 \\\ln(x+a)=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=\pm \sqrt{5} \\x_{2}=1-a \end{matrix}\right.$$

$$\sqrt{5}\in [0; 3]$$, тогда есть три возможных варианта ($$x_{2}\in$$ ОДЗ при всех a)

1) $$x_{1}\notin$$ ОДЗ и $$x_{2}\in [0 ;3]$$

$$\left\{\begin{matrix}\sqrt{5}\leq -a \\0\leq1-a\leq 3 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a\leq -\sqrt{5} \\-2\leq \leq 2\end{matrix}\right.\Leftrightarrow$$ $$\varnothing$$

2) $$x_{1}\in$$ ОДЗ и $$x_{2}\notin [0 ;3]$$

$$\left\{\begin{matrix}\sqrt{5}>- a \\\left\{\begin{matrix}1-a>3 \\1-a<0 \end{matrix}\right. \end{matrix}\right.\Leftrightarrow$$

$$\left\{\begin{matrix}a>-\sqrt{5} \\\left\{\begin{matrix}a<-2 \\a>1 \end{matrix}\right. \end{matrix}\right.\Leftrightarrow$$$$a\in (-\sqrt{5};-2)\cup (1; +\infty )$$

3) $$x_{1}=x_{2}$$

$$1-a=\sqrt{5}\Leftrightarrow 1-\sqrt{5}$$

Объединим полученные результаты: $$a\in (-\sqrt{5};-2)\cup (1-\sqrt{5})\cup (1; +\infty)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}x^{2}+y^{2}-2ax+2ay\leq 0 \\x^{2}+y2 +6ax+8ay\leq 1-10a \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x^{2}-2ax+a^{2}+y^{2}+2ay+a^{2}-2a^{2}\leq 0 \\x^{2}+6ax+9a^{2}+y^{2}+8ay+16a^{2}-25a^{}\leq 1-10a \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}(x-a)^{2}+(y+a)^{2}\leq 2a^{2}(f(x)) \\(x+3a)^{2}+(y+4a)^{2}\leq 25a^{2}-10a+1(g(x)) \end{matrix}\right.$$

f(x)-окружность с центром (a;-a) и $$r=\sqrt{2}|a|$$

g(x)-окружность с центром (-3a;-4a) и $$r=|5a-1|$$??

Чтобы было одно решение, расстояние между центральным равно сумме радиусов(т.к. окружности касается)

$$\sqrt{(-3a-a)^{2}+(-4a-(-a))^{2}}=\left | 5a-1 \right |+\sqrt{2}\left | a \right |$$

$$\sqrt{25a^{2}}=\left | 5a-1 \right |+\sqrt{2}\left | a \right |$$

$$5|a|-\sqrt{2}|a|=|5a-1|$$

1) $$\left\{\begin{matrix}a\leq 0 \\-5a+\sqrt{2}a=-5a+1 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a\leq 0 \\a=\frac{1}{\sqrt{2}} \end{matrix}\right.\Leftrightarrow$$ $$\varnothing$$

2)$$\left\{\begin{matrix}a \in (0;0,2] \\5a-\sqrt{2}a=-5a+1 \end{matrix}\right.\Leftrightarrow$$ $$10a-\sqrt{2}a=1\Leftrightarrow$$$$a=\frac{1}{10-\sqrt{2}}$$

3) $$\left\{\begin{matrix}a>0,2 \\5a-\sqrt{2}a=5a-1 \end{matrix}\right.\Leftrightarrow$$ $$\sqrt{2}a=1\Leftrightarrow$$ $$a=\frac{\sqrt{2}}{2}$$

Объединим полученные значения: $$\frac{1}{10-\sqrt{2}} ;\frac{\sqrt{2}}{2}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

В исходном уравнении $$4^{1-x^{2}}-3a^{2}*2^{1-x^{2}}+3a^{2}-a^{2}=0$$ выполним замену переменной $$t=2^{1-x^{2}}$$. Получим уравнение  $$t^{2}-3a^{2}t+3a^{3}-a^{2}=0$$. В этом уравнении $$t>0$$

Поскольку $$1-x^{2}\leq 1$$ имеем : $$2^{1-x^{2}}\leq 2\Leftrightarrow t\leq 2$$. Если $$x_{0}\neq 0$$ является корнем исходного уравнения, то и $$-x_{0}$$-также является его корнем. Следовательно, преобразовательное уравнение должно иметь ровно один корень в промежутке (0;2]. Более того, если 2- корень преобразованного уравнения , то исходное уравнение имеет нечётное количество корней , т.к. равенство $$2^{1-x^{2}}=2$$ выполняется только при $$x=0$$

1)Преобразованное уравнение имеет единственный корень при $$D=0$$, т.е. $$D=9a^{4}-12a^{3}+4a^{2}=a^{2}(3a-2)^{2}=0$$

При $$a=0$$ получаем $$t=0\notin (0;2)$$ . При $$a=\frac{2}{3}$$ получаем $$(t-\frac{2}{3})^{2}=0\Leftrightarrow t=\frac{2}{3}$$-решение задачи

$$a =\frac{2}{3}$$

2) Обозначим $$f(t)=t^{2}-3a^{2}+3a^{3}-a^{2}$$ и рассмотрим теперь промежуток (0;2) для значений корня преобразованного уравнения. Обозначим $$f(t)=t^{2}-3a^{2}t+3a^{3}-a^{2}$$

Для того, чтобы единственный корень этого уравнения попадал в указанный промедуток , досаточно, чтобы a\neq 0

$$\left[\begin{matrix}\left\{\begin{matrix}f(0)>0\\f(2)<0\end{matrix}\right.\\\left\{\begin{matrix}f(0)<0\\f(2)>0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}(a-1)(a-2)(a+\frac{2}{3})<0\\a^{2}(a-\frac{1}{3})>0\end{matrix}\right.\\\left\{\begin{matrix}(a-1)(a-2)(a+\frac{2}{3})>0\\a^{2}(a-\frac{1}{3})<0\end{matrix}\right.\end{matrix}\right.$$

Остается рассмотреть случай $$a=\frac{1}{3}$$. В этом случае преобразованное уравнение принимает

 Вид $$t(t-\frac{1}{3})=0$$, откуда $$t=\frac{1}{3}$$-единственный корень в промежутке (0;2) , т.е.

$$a=\frac{1}{3}$$-решение задачи

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Преобразуем данное неравенство: $$(a-7)(3a-8(2^{x}+1))\leq 8x(x-2)(2^{x}+1)-3ax(x-2) \Leftrightarrow$$$$(a-7)(3a-8(2^{x}+1))\leq x(x-2)(8(2^{x}+1)-3a) \Leftrightarrow$$$$(a-7)(3a-8(2^{x}+1)) + x(x-2)(3a-(2^{x}+1))\leq 0 \Leftrightarrow$$$$(8(2^{x}+1)-3a)(x^{2}-2x+a-7) \geq 0 (1)$$

Рассмотрим по отдельности обе скобки и представим их как функции $$a(x)$$:

$$8(2^{x}+1)-3a = 0\Leftrightarrow$$$$a=\frac{2^{x+3}}{3}+\frac{8}{3}$$ - график степенной функции

$$x^{2}-2x+a-7=0 \Leftrightarrow$$$$a=-x^{2}+2x+7\Leftrightarrow$$$$a=-(x^{2}-2x-7)\Leftrightarrow$$$$a=-(x^{2}-2x+1-1-7)\Leftrightarrow$$$$a=-(x-1)^{2}+8$$ - график квадратичной функции.

По условии задачи необходимо, чтобы решения были на промежутке $$[-1;0)$$, тогда так же построим графики $$x=-1 ; x=0$$ и графики полученных функции в системе координат AoX.

Найдем пересечение степенной функции с прямыми $$x=-1 ; x=0$$:

$$x=-1 ; a(-1)=\frac{2^{-1+3}}{3}+\frac{8}{3}=4$$

$$x=0 ; a(0)=\frac{2^{0+3}}{3}+\frac{8}{3}=\frac{16}{3}$$

Как видим по графикам мы получили три области, необходимо проверить, точки каких областей удовлетворяют неравенству (1). Для этого будем брать из каждой области точку, и подставлять координаты в наше неравенство:

1) Возьмем точку (0;0) : $$(8(2^{0}+1)-3*0)(0^{2}-2*0+0-7) \geq 0 \Leftrightarrow$$$$16*(-7)\geq 0$$ - неравенство неверно, следовательно, первая область не подходит

2) Возьмем точку (0;6): $$(8(2^{0}+1)-3*6)(0^{2}-2*0+6-7) \geq 0 \Leftrightarrow$$$$-2*(-1)\geq 0$$ - неравенство верно, следовательно, вторая область подходит и по а она находится в промежутке [4;7) (7 не входит, так как по условию $$x \neq 0$$)

3) Возьмем точку (0;8) : $$(8(2^{0}+1)-3*8)(0^{2}-2*0+8-7) \geq 0 \Leftrightarrow$$$$-8*1 \geq 0$$ - неравенство неверно, следовательно, третья область не подходит

Итоговый ответ: $$a \in \left [ 4 ; 7 \right )$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Рассмотрим каждую скобку по отдельности. Так как произведение равно нулю, когда один из множителей равно нулю, то итоговым решением будет совокупность решений каждой скобки:

Пусть : $$|2x+1-a|+|2x+1+a|-2a=0 (A)$$ или $$|x^{2}-2x+a|+|x^{2}-2x-a|-2a=0 (B)$$

A) Раскроем модули. Модули равны 0, если $$2x+1=\pm a$$. Отметим данные значения на координатной прямой, рассмотрим, какие знаки принимают подмодульные выражения:

Итоговой областью решения будет множество точек объединения получившихся промежутков (фиолетовая область):

Наим необходимо, чтобы было ровно 4 целых значения х. Построим прямую $$a=0,5$$ Как видим, целых абсцисс, попавших в пересечение прямой и области решения всего 2 ( 0 и 2). Построим прямую $$a=1$$. Как видим, целых абсцисс получаем 4 (-1 ; 0 ; 1 ; 2). Построим прямую $$a=3$$, там уже будет 6 целых абсцисс (-2 ; -1 ; 0 ; 1 ; 2 ; 3). Следовательно, решением будет $$a \in [1 ; 3)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Преобразуем данное уравнение относительно переменной а (х будет параметром): $$x^{4}-2x^{3}-(2a+3)x^{2}+2ax+3a+a^{2}=0\Leftrightarrow$$$$x^{4}-2x^{3}-2ax^{2}+3x^{2}+2ax+3a+a^{2}=0\Leftrightarrow$$$$a^{2}+a(3+2x-2x^{2})+x^{4}-2x^{3}-3x^{2}$$

Найдем корни данного уравнения:

$$D=(3+2x-2x^{2})^{2}-4(x^{4}-2x^{3}-3x^{2})=4x^{2}+12x+9=(2x+3)^{2}$$

$$a_{1}=\frac{2x^{2}-2x-3+|2x+3|}{2}$$

$$a_{2}=\frac{2x^{2}-2x-3-|2x+3|}{2}$$

Рассмотрим график функции $$a_{1}(x)$$, раскроем модуль:

$$\left\{\begin{matrix}x\geq -1,5\Rightarrow a=x^{2}\\x< -1,5\Rightarrow a=x^{2}-2x-3\end{matrix}\right.$$

Рассмотрим график функции $$a_{2}(x)$$, раскроем модуль:

$$\left\{\begin{matrix}x\geq -1,5\Rightarrow a=x^{2}-2x-3\\x< -1,5\Rightarrow a=x^{2}\end{matrix}\right.$$

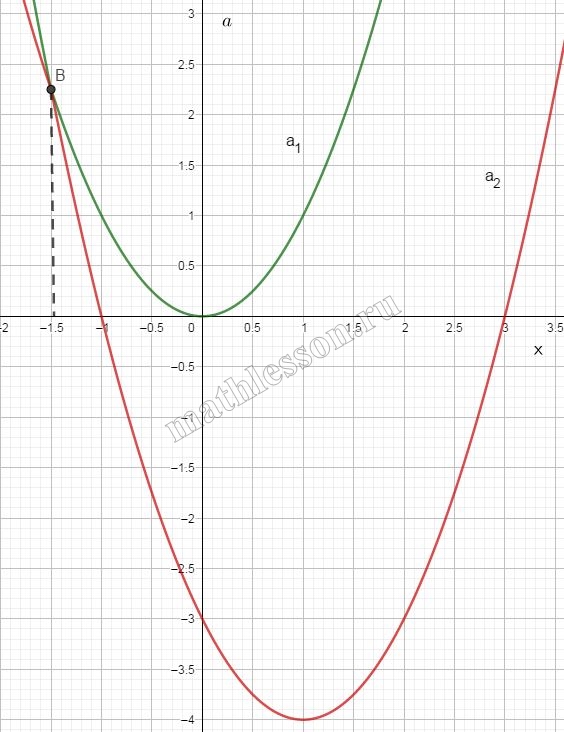
Построим графики функций $$a_{1}(x);a_{1}(x)$$:

Как видим, значения $$a$$ начинаются с -4 (вершина параболы $$a_{2}(x)$$). С учетом свойств квадратичной функции, получаем, что $$a \geq -4$$. При этом значение х, пределяемое единственным значением а равно -1,5 (абсцисса точки пересечение графиков обеих квадратичных фукнций)

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$a ^{2}+8\left | x-5 \right |+2\sqrt{x^{2}-10x+29}=2a +\left | x-2a -5 \right |$$

Пусть x-5=y

$$a ^{2}+8\left | y \right |+2\sqrt{y^{2}+4}=2a +\left | y-2a \right |$$

$$2\sqrt{y^{2}+4}= 2a -a ^{2}-8\left | y \right |+\left | y-2a \right |$$

Рассмотрим обе части уравнения как отдельные функции g(y) и f(y):

$$g(y)=2\sqrt{y^{2}+4}$$ - график данной функции - ветви параболы

При этом минимальное значение будет: $$g_{min}=g(0)=2\sqrt{0+4}=4$$

Рассмотрим функцию f(y): так как там есть модуль и параметр, то будет несколько вариантов раскрытия:

$$f(g)=2a -a ^{2}-8\left | y \right |+\left | y-2a \right |$$ - кусочно-линейная функция

а)Пусть $$2a \geq 0$$, тогда

1)$$y\leq 0$$ $$f(y)=2a -a ^{2}+8y-y+2a =7y+4a -a ^{2}$$ - синий цвет

2)$$y\in (0 ; 2a )$$ $$f(y)=2a -a ^{2}-8y-y+2a =-9y+4a -a ^{2}$$ - зеленый цвет

3) $$y> 2a$$ $$f(y)=2a -a ^{2}-8y+y-2a =-7y-a ^{2}$$ - красный цвет

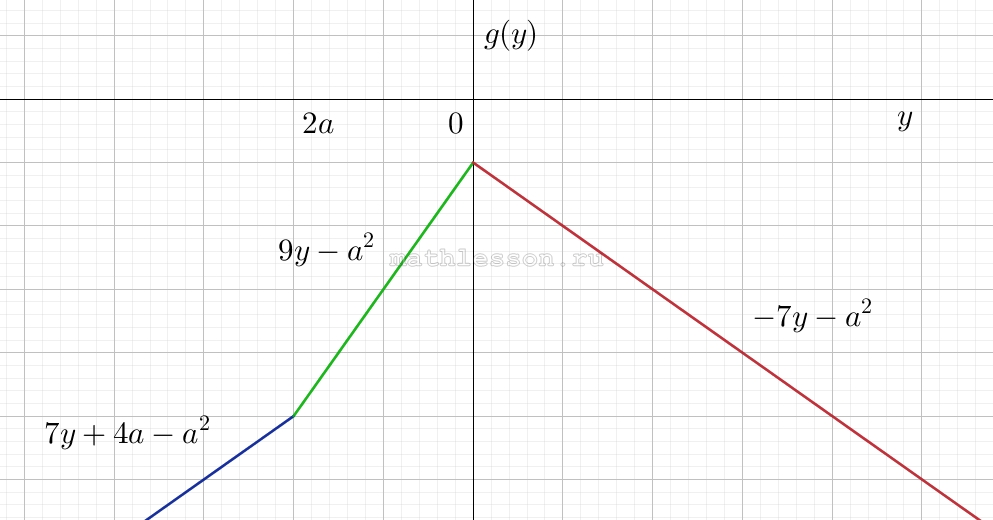
Схематичное изображение графика:

Как видим максимальное значение в координате $$y=0$$: $$f_{max}=f(0)=2a =a ^{2}+\left | -2a \right |$$

б)Пусть $$2a < 0$$

1)$$y\leq 2a$$ $$f(y)=2a -a ^{2}+8y-y+2a =7y+4a -a ^{2}$$

2)$$y\in (2a; 0)$$ $$f(y)=2a -a ^{2}+8y+y-2a =9y-a ^{2}$$

3)$$y\geq 2a$$ $$f(y)=2a -a ^{2}-8y+y-2a =-7y-a ^{2}$$

Схематичное изображение графика:

И тут максимальное значение в координате $$y=0$$: $$f_{max}=f(0)$$. То есть, независимо от значения $$a$$ максимальное значение при $$y=0$$.

Тогда , чтобы были решения $$g_{min}\leq f_{max}$$ (графическая интерпритация):

Тогда:

$$4\leq 2a -a ^{2}+\left | -2a \right |\Leftrightarrow$$$$a ^{2}-2a -\left |- 2a \right | +4\leq 0$$

Расскроем модуль:

1)$$-2a \geq 0\Rightarrow a \leq 0$$. Тогда $$a ^{2}-2a +2a +4\leq 0\Rightarrow a ^{2}+4\leq 0\Rightarrow$$ решений нет

2) $$-2a < 0\Rightarrow a > 0$$. Тогда $$a ^{2}-2a -2a +4\leq 0\Rightarrow (a -2)^{2}\leq 0\Rightarrow a =2$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}y=2ax-2x^{2}+60-4 & & \\y=\frac{3*3^{x^{2}}}{27^{a}}-\frac{3^{ax}}{3}& &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}y_{1}=2(-x^{2}+ax+3a-2) & & \\y_{2}=3^{x^{2}-3a+1}-3^{2x-1} & &\end{matrix}\right.$$

Рассмотрим монотонность $$y_{2}$$:

$$3^{x^{2}-3a+1}-3^{ax-1}>0$$

$$3^{x^{2}-3a+1}>3^{ax-1}$$

$$x^{2}-3a+2>0$$

$$x^{2}-ax-3a+2>0$$

Пусть $$x^{2}-ax-3a+2=f$$. Тогда $$y_{1}=-2f$$. Получаем, если $$f>0$$,то $$y_{2}>0$$, но $$y_{1}<0$$ ,и наоборот . Тогда $$y_{1}=y_{2}$$ только при условии , что $$f=0$$.

$$x^{2}-ax-3a+2=0$$

$$D=a^{2}-4(2-3a)=a^{2}+12a-8>0$$

$$D=144+32=176$$

$$a_{1,2}=\frac{-12\pm \sqrt{176}}{2}=-6\pm \sqrt{44}=-6\pm 11$$, тогда

$$a\in (-\infty; -6;-\sqrt{11})\cup (-6; +\sqrt{11};+\infty )$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}x^{2}+5x+y^{2}-y-\left | x-5y+5 \right |=52|(f)\\y-2=a(x-5)|(g)\end{matrix}\right.$$

Рассмотрим варианты раскрытия модуля:

   1) При $$x-5y+5\geq 0\Leftrightarrow y\leq \frac{x}{5}+5$$

$$f_{1}:x^{2}+5x+y^{2}-y-x+5y-5=52$$

$$x^{2}+4x+4-4+y^{2}+4y+4-4-5=52$$

$$(x+2)^{2}+(y+2)^{2}=65$$-окружность с центром (-2 ;-2) и радиусом $$\sqrt{65}$$

   2) При $$x-5y+5<0\Leftrightarrow y>\frac{x}{5}+5$$

$$f_{2}: x^{2}+5x+y^{2}-y+x-5y+5=52$$

$$x^{2}+6x+9-9+y^{2}-6y+9-9+5=52$$

$$(x+3)^{2}+(y-3)^{2}=65$$ - окружность с центром $$(-3;3)$$ и радиусом $$\sqrt{65}$$

   При этом $$g: y=a(x-5)+2$$-прямая, проходящая через точку

   Построим график обеих функций:

Чтобы прямая y=a(x-5)+2 имела 2 точки, то :

   $$a \in (b_{1}; \frac{1}{5})$$, где $$b_{1}$$-коэффициент касательной $$y=b_{1}x+n_{1}(1)$$k и $$a \in (\frac{1}{5};b_{2})$$, где $$b_{2}$$- коэффициент касательной $$y=b_{2}x+n_{2}(2)$$(в обоих случаях касательная в точке (5;2))

   1) Посмотрим радиус $$O_{2}A$$ . Задаем коэффициент k данной прямой $$f=\frac{4}{7}$$, при этом  $$y=b_{1}x+n_{1}\perp O_{1}A\Rightarrow k*b_{1}=-1\Rightarrow b_{1}=-\frac{7}{4}$$

   2) Аналогично $$O_{2}A$$: $$k=-\frac{1}{8}\Rightarrow b_{2}=8$$

   В итоге получаем: $$a\in (-\frac{7}{4}; 8)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}(4-x^{2}-y^{2})(y^{2}-4x+28)=0 \\x \cos \alpha +y \sin \alpha =2\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}x^{2}+y^{2}=4\\x \cos \alpha +y \sin \alpha =2 (1)\end{matrix}\right.\\\left\{\begin{matrix}y^{2}-4x+8-0\\x \cos \alpha +y \sin \alpha =2 (2)\end{matrix}\right.\end{matrix}\right.$$

Рассмотрим систему (1) :

$$x \cos \alpha +y \sin \alpha =2\Leftrightarrow y=\frac{-x \cos \alpha +2}{\sin \alpha }=-ctg \alpha *x+\frac{2}{\sin \alpha }$$. Построим данную прямую . Она смешена по Oy на $$\frac{2}{\sin \alpha }$$

Пусть $$\angle OAB=\alpha$$, тогда $$\angle BCO=90-\alpha$$ , и смежный с ним $$\alpha -90$$. Для прямой $$y=kx+b; k=tg \beta$$ ,где $$\beta$$-угол между прямой и Ox: $$tg(\alpha -90)=-ctg \alpha$$

Длина OB из $$\Delta ABO: OA*\sin \alpha =\frac{2}{\sin \alpha }*\sin\alpha =2$$ Т.е. независимо от $$\alpha$$ , длина OB всегда что составляет радиус окружности $$x^{2}+y^{2}=4$$. Т.е. $$y=-ctg \alpha *x+\frac{2}{\sin \alpha }$$ при всех $$\alpha$$ - касательная ,следовательно, одно решения есть.

Рассмотрим систему (2):она должна иметь ровно 2 решения :

$$\left\{\begin{matrix} y^{2}-4x+28=0 & & \\ x \cos \alpha +y \sin \alpha =2 & & \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} y^{2}-4*\frac{2-y \sin \alpha }{\cos ^{2}}+28=0 & & \\ x=\frac{2-y\sin \alpha }{\cos x}& & \end{matrix}\right.$$

Учитываем ,что: $$\cos \alpha \neq 0\Leftrightarrow \alpha \neq \frac{\pi}{2}+\pi n , n \in Z$$

$$y^{2}-*\frac{4*(2-y \sin\alpha )}{\cos \alpha }+28=0$$

$$y^{2}\cos \alpha -8+4y \sin \alpha +28 \cos \alpha =0$$

Чтобы было два решения, дискриминант должен быть строго больше 0:

$$D=(4 \sin \alpha )^{2}-4 \cos \alpha (28 \cos \alpha -8)>0$$

$$16 \sin^{2}\alpha -16 \cos\alpha (7\cos\alpha -2)>0$$

$$\sin^{2}-7\cos^{2}\alpha +2\cos\alpha >0$$

$$1-\cos^{2}\alpha -7 \cos ^{2}\alpha +2 \cos \alpha >0$$

$$8 \cos^{2}-2 \cos \alpha -1<0$$

$$D=4+32=36$$

$$\cos \alpha =\frac{2+6}{16}=\frac{1}{2}$$ и $$\cos \alpha =\frac{2-6}{16}$$

Получаем: $$\left\{\begin{matrix}\cos \alpha >-\frac{1}{4} & & \\\cos \alpha <\frac{1}{2} & &\end{matrix}\right.$$. Учтем ,что $$\alpha \in (-\pi; \pi) \alpha \neq \frac{\pi}{2}+\pi n$$

$$\alpha \in (-\pi +\arccos\frac{1}{4}; -\frac{\pi}{2})\cup (-\frac{\pi}{2};-\frac{\pi}{3})\cup (\frac{\pi}{3};\frac{\pi}{2})\cup (\frac{\pi}{2} ;\pi-\arccos \frac{1}{4})$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$D(f):\left\{\begin{matrix} x>0 \\ 25x\neq 1 \end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix} x>0 \\ x\neq \frac{1}{25} \end{matrix}\right.$$

1) Пусть $$a=\pm 1$$,тогда $$\log_{5}x=2\Leftrightarrow x=25$$ - один корень, что не устраивает условие задания

2) Пусть $$a\neq \pm 1$$, тогда: $$\log_{5}x+\frac{4(1-a^{2})}{\log_{5}25x}-2=0\Leftrightarrow$$$$\log_{5}x+\frac{4(1-a^{2})}{\log_{5}x+2}-2=0\Leftrightarrow$$$$\log_{5}^{2}x+2\log_{5}x-2\log_{5}x-4+4-4a^{2}=0\Leftrightarrow$$$$\log_{5}^{2}x=4a^{2}\Leftrightarrow$$$$\left\{\begin{matrix} \log_{5}x=2a\\ \log_{5}x=-2a\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} x_{1}=5^{2a}\\ x_{2}=5^{-2a}\end{matrix}\right.$$

Так как по условию задания $$\left | x_{1}-x_{2} \right |>\frac{24}{5}$$ тогда: $$\left | 5^{2a}-5^{-2a} \right |\Leftrightarrow$$. Пусть $$5^{2a}=y>0$$, тогда:

$$\left | y-\frac{1}{y} \right |>\frac{24}{5}\Leftrightarrow$$ $$\left[\begin{matrix} y-\frac{1}{y}>\frac{24}{5}\\ y-\frac{1}{y}<\frac{-24}{5}\end{matrix}\right.$$$$\Leftrightarrow \left[\begin{matrix} \frac{5y^{2}-24y-5}{y}>0 \\ \frac{5y^{2}+24y-5}{y}<0 \end{matrix}\right.$$

т.к. y>0, то $$\left[\begin{matrix} 5y^{2}-24y-5>0 \\ 5y^{2}+24y-5<0 \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} (y-5)(y+\frac{1}{5})>0 \\ (y+5)(y-\frac{1}{5})<0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} y-5>0 \\ y-\frac{1}{5}<0 \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} y>5 \\ y<\frac{1}{5} \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} 5^{2a}>5 \\ 5^{2a}<\frac{1}{5} \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} a>\frac{1}{2} \\ a<-\frac{1}{2} \end{matrix}\right.$$

С учётом , что $$a\neq \pm 1$$, получаем: $$a\in (-\infty ;-1)\cup (-1; -\frac{1}{2})\cup (\frac{1}{2}; 1)\cup (1 ;+\infty )$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

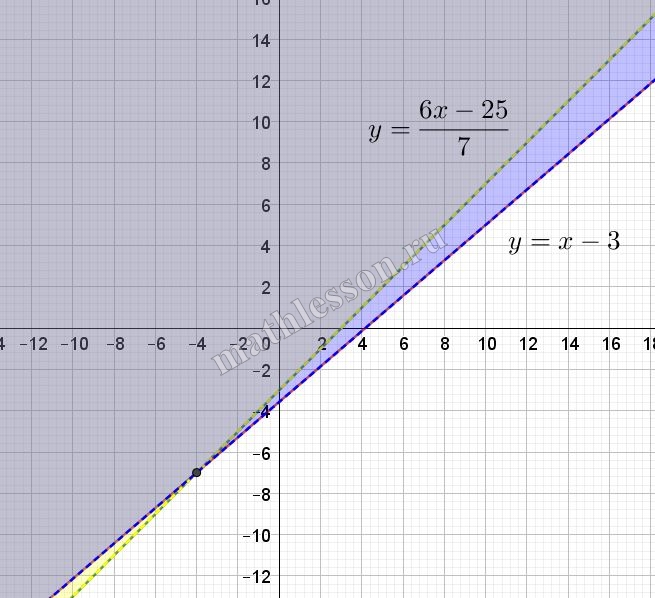
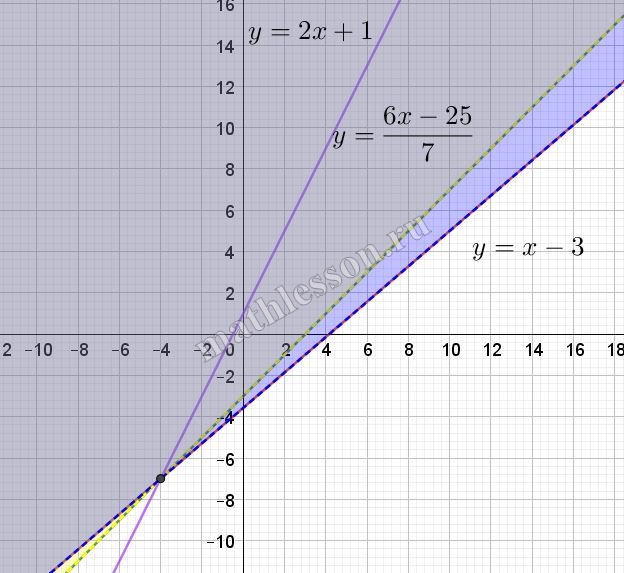
     Рассмотрим область определения данной системы. Так как даны логарифмы, то: $$\left\{\begin{matrix}3-x+y>0\\25-6x+7y>0\end{matrix}\right.\Rightarrow$$ $$\left\{\begin{matrix}y>x-3\\y>\frac{6x-25}{7}\end{matrix}\right.$$ (желтым выделено решение для первого неравенства, синим - для второго, серым - их пересечение)

     Рассмотрим первое уравнение системы:

$$\log_{2}(8(3-x+y))=\log_{2}(25-6x+7y)\Leftrightarrow$$$$24-8x+8y=25-6x+7y\Leftrightarrow$$$$y=2x+1 (1)$$

     Построим график данной функции с учетом области определения:

     Как видим, чтобы было два пересечения, x должен быть больше 4 (иначе часть прямой лежит вне области определения)

     Подставим  (1) во второе:$$2+2x+1=(x-2a)^{2}+a+2x\Leftrightarrow$$$$(x-2a)^{2}=3-a$$

     Так как число в квадрате, то правая часть уравнения должна быть больше нуля (если равна нулю, то корень всего один): $$3-a>0\Rightarrow a<3$$

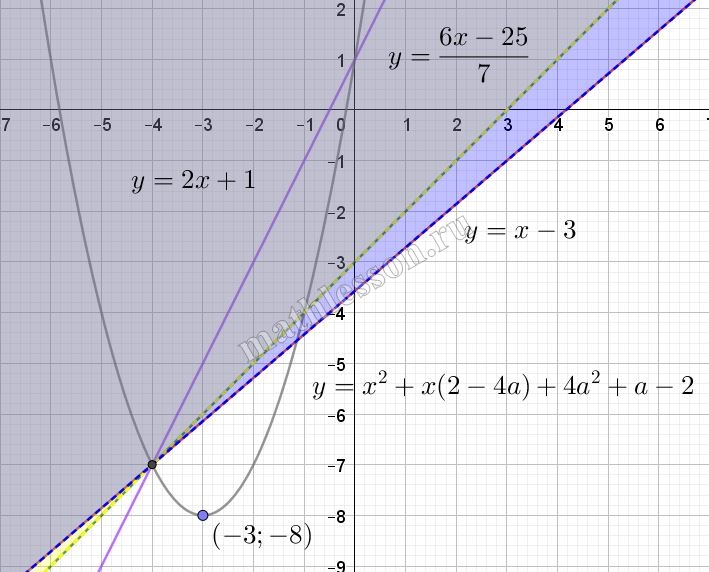
     Рассмотрим график второй функции:

$$y+2=x^{2}-4ax+2a^{2}+a+2x\Leftrightarrow$$$$y=x^{2}+x(2-4a)+4a^{2}+a-2$$

     Найдем вершину параболы:

$$x_{0}=-\frac{2(1-2a)}{2}=2a-1$$

$$y_{0}=4a^{2}-4a+1-2(2a-1)^{2}+4a^{2}+a-2=8a^{2}-3a-1-8a^{2}+8a-2=5a-3$$

     Рассмотрим возможное расположение графика с учетом области определения:

     Как видим, координата y вершины параболы должна быть больше -8, а х больше -3 (если будет левее, то отно пересечение точно не попадет в область определения) :

$$\left\{\begin{matrix}2a-1>-3\\5a-3>-8\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a>-1\\a>-1\end{matrix}\right.$$

     С учетом того, что $$a<3$$, получаем: $$a \in (-1;3)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left\{\begin{matrix}\left | x \right |+2\left | y \right |+\left | 2y-3x \right | =12=f\\x^{2}+y^{2}=a=g\end{matrix}\right.$$

g - окружность с центром в начале координат и радиуса $$\sqrt{a}\Rightarrow a>0$$

     Рассмотрим график f:

При $$2y-3x\geq 0\Leftrightarrow$$ $$y\geq 1,5 x$$ получили $$\left | x \right |+2\left | y \right |+ 2y-3x =12$$

     В данном случае будет 3 части плоскости:

1)$$\left\{\begin{matrix}x\geq 0\\y\geq 0\end{matrix}\right.\Rightarrow$$ $$x+2y+2y-3x=12\Leftrightarrow$$ $$y=3+0,5x$$

2)$$\left\{\begin{matrix}x<0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$-x+2y+2y-3x=12\Leftrightarrow$$ $$y=3+x$$

3)$$\left\{\begin{matrix}x<0\\y<0\end{matrix}\right.\Leftrightarrow -x-2y+2y-3x=12\Rightarrow x=-3$$

     При $$2y-3x<0\Leftrightarrow y<1,5x$$ получим так же 3 части плоскости:

1)$$\left\{\begin{matrix}x\geq 0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$x+y-2y+3x=12\Leftrightarrow x=3$$

2)$$\left\{\begin{matrix}x\geq 0\\y<0\end{matrix}\right.\Leftrightarrow$$ $$x-y-2y+3x=12\Leftrightarrow y=-3+x$$

3)$$\left\{\begin{matrix}x<0\\y<0\end{matrix}\right.\Leftrightarrow$$ $$-x-y-2y+3x=12\Leftrightarrow y=x-3$$

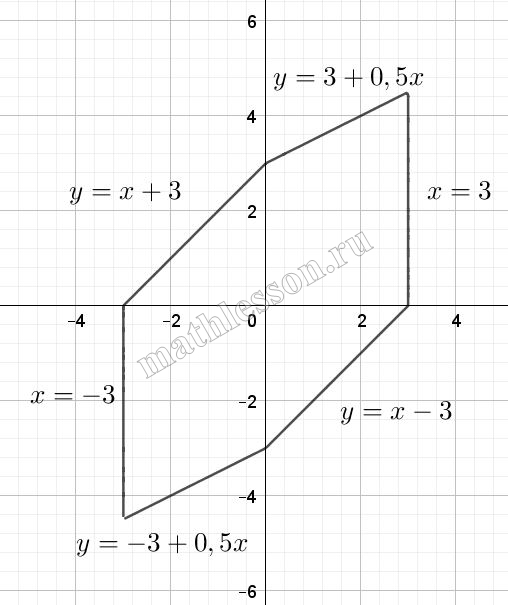
     Построим график данной функции .

     Очевидно , что 2 точки будет если пройдет через (C) и если касается в (B)

     Найдем координаты (C) :$$y=3+0,5=4,5$$.

Тогда $$OC=r_{1}^{2}=a=3^{2}+4,5^{2}=29,25$$. Найдем $$OB=r_{2}^{2}=a=1,5^{2}+1,5^{2}=4,5.$$