ЕГЭ Профиль
Задание 4366
В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 4. Точка L — середина ребра SC. Тангенс угла между прямыми BL и SA равен $$\frac{2\sqrt{34}}{17}$$
Задание 4396
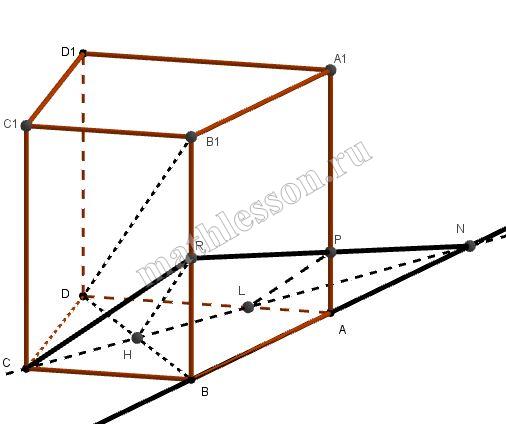
В основании пирамиды TABCD лежит трапеция ABCD , в которой $$BC\parallel AD$$ и AD:BC=2. Через вершину Т пирамиды проведена плоскость, параллельная прямой ВС и пересекающая отрезок АВ в точке М такой, что АМ:MB=2. Площадь получившегося сечения равна 10, а расстояние от ребра ВС до плоскости сечения равно 4.
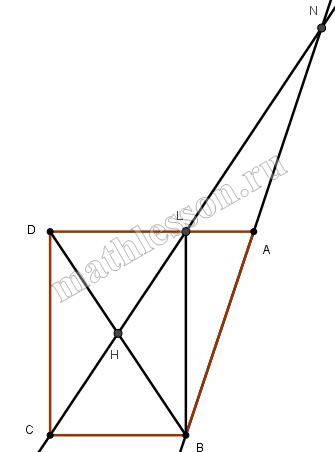
а) 1) Построим через М прямую $$\parallel BC$$ $$\Rightarrow$$ $$MN\parallel BC$$ $$\Rightarrow$$ $$(TMN)$$ - сечение
2) Опустим высоту ВН в трапеции ABCD: $$BH\cap MN=O$$ $$\Rightarrow$$ $$BO=h$$; $$\bigtriangleup MBO\sim\bigtriangleup ABH$$ (по острому углу и прямому) $$\Rightarrow$$ $$\frac{BO}{OH}=\frac{BM}{AM}=\frac{1}{3}$$ $$\Rightarrow$$ $$OH-2BO=2h$$
3) Опустим $$CK\perp CD$$; $$CK\cap MN=R$$: $$BC=OR=HK=x$$ $$\Rightarrow$$ Пусть $$CH=a$$ $$\Rightarrow$$ $$KD=x-a$$. Тогда из подобия $$\bigtriangleup MBO\sim\bigtriangleup ABH$$: $$MO=\frac{1}{3}CH=\frac{1}{3}a$$; аналогично $$RN=\frac{1}{3}KD=\frac{1}{3}x-\frac{1}{3}a$$. Tогда $$MN=MO+OR+RN=\frac{1}{3}a+x+\frac{1}{3}x-\frac{1}{3}a=\frac{4}{3}x$$
4) $$S_{MBCN}=\frac{BC+MN}{2}\cdot BO=$$ $$\frac{x+\frac{4}{3}x}{2}\cdot h=\frac{7xh}{6}$$; $$S_{AMND}=\frac{AD+MN}{2}\cdot OH=$$ $$\frac{2x+\frac{4}{3}x}{2}\cdot2h=\frac{20xh}{6}$$ $$\Rightarrow$$ $$\frac{V_{MBCNT}}{V_{AMNDT}}=\frac{S_{MBCN}}{S_{AMND}}=$$ $$\frac{7xh}{6}\div\frac{20xh}{6}=\frac{7}{20}$$
б) 1) Пусть расстояние от ВС до $$MTN=d$$ (т.к. у них общая вершина): $$V_{BMNT}=\frac{1}{3}S_{MTN}\cdot d=\frac{1}{3}\cdot10\cdot4=\frac{40}{3}$$
2) $$\frac{V_{BNMT}}{V_{BCNMT}}=\frac{S_{BNM}}{S_{BCNM}}=$$ $$\frac{\frac{1}{2}\cdot MN\cdot BO}{\frac{MN+BC}{2}\cdot BO}=$$ $$\frac{\frac{1}{2}\cdot\frac{4x}{3}}{\frac{x+\frac{4x}{3}}{2}}=\frac{4}{7}$$ $$\Rightarrow$$ $$V_{BCNMT}=\frac{7}{4}V_{BNMT}=\frac{70}{3}$$
3) $$V_{AMNDT}=\frac{20}{7}V_{BCNMT}=\frac{70}{3}\cdot\frac{20}{7}=\frac{200}{3}$$
4) $$V_{ABCDT}=V_{AMNDT}+V_{BCNMT}=\frac{70}{3}+\frac{200}{3}=90$$
Задание 4573
В правильной шестиугольной пирамиде $$PABCDEF$$ боковое ребро наклонено к основанию под углом $$\alpha=\arctan\frac{\sqrt{3}}{2}$$.
Задание 4669
Основанием пирамиды FABCD является квадрат ABCD. На ребре AF взята точка Е такая, что отрезок СЕ перпендикулярен ребру AF. Проекция О точки Е на основание пирамиды лежит на отрезке АС и делит его в отношении AO:OC=4:1. Угол ADF равен 900.
Задание 4819
Сторона основания правильной треугольной призмы АВСА1В1С1 равна $$10\sqrt{3}$$ , а высота СС1 равна 7,5. На ребре В1С1 отмечена точка Р так, что В1Р:РС1=1:3. Точки Q и М являются серединами сторон АВ и А1С1 соответственно. Плоскость $$\alpha$$ параллельна прямой АС и проходит через точки Р и Q.
А) 1) $$a\cap (ABC)=QT\left |\right |AC$$, $$a\cap (A_{1}B_{1}C_{1})=PN\left |\right |A_{1}C_{1}$$, т.к. $$a\left |\right |AC. a\cap (BGM)=EF$$, $$BM\cap EF=S$$( E и F-середины PN и QT). BM-наклонная , BG-её проекция , $$BG\perp QT\Rightarrow$$ по т. о трёх перпендикулярах $$BM\perp QT(1)$$
2) $$\angle SBF =\beta$$ , $$\angle BFS=\gamma$$ , $$\angle BSF=\varphi$$; $$BG=AB*\sin 60=10\sqrt{3}*\frac{\sqrt{3}}{2}=15$$; $$tg\beta =\frac{MG}{BG}=\frac{7,5}{15}=\frac{1}{2}$$; $$ctg\gamma =\frac{\frac{1}{2}BF}{BB_{1}}=$$$$\frac{1}{4}*\frac{15}{7,5}=$$$$\frac{1}{2}=tg\beta \Rightarrow$$ $$\beta +\gamma =90$$, тогда $$\varphi =90$$, $$BM\perp EF(2)$$ . Из (1) и (2) $$\Rightarrow$$ $$BM\perp \alpha$$
Б) 1) из п. а) $$BM\perp \alpha \Rightarrow$$ $$p(Ma)=MS$$
2) $$\Delta ESM\sim \Delta FSB$$ по двум углам $$\Rightarrow$$ $$\frac{MS}{BS}=\frac{ME}{BF}=\frac{3}{2}$$, тогда $$MS=\frac{3}{5}BM$$; $$BM=\sqrt{BG^{2}+MG^{2}}=\sqrt{225+\frac{225}{4}}=\frac{15\sqrt{5}}{2}$$, $$MS=\frac{3}{5}*\frac{15\sqrt{5}}{2}=\frac{9\sqrt{5}}{2}$$
Задание 4863
а) 1) Достроим AE до пересечения с BC в точке N. Тогда $$(AMN)=\alpha$$
2) $$\bigtriangleup AED \sim \bigtriangleup BFE$$ (по двум углам). Тогда $$\frac{BE}{ED}=\frac{BF}{AD}\Leftrightarrow $$$$BF=\frac{BE*AD}{ED}=\frac{1}{2}*12=6$$
3)$$AB=BF; BG\perp (ABC);BG$$-общая, значит $$\bigtriangleup ABG =\bigtriangleup GBF ; AG = GF$$
б)1)Расстояние от B до плоскости сечения такое же, как и от B1. Построим $$BH \perp AF$$: $$BH=\frac{1}{2}AF$$ ($$\bigtriangleup ABF$$ - прямоугольный и равнобедренный). $$BH = \frac{1}{2}*\sqrt{6^{2}+6^{2}}=3\sqrt{2}$$
2) Построим $$BF \perp GH ; BR \perp AF$$ (т.к. $$BH \perp AF$$, то по теореме о трех перпендикулярах). Тогда $$BR \perp \alpha$$, значит BR - расстояние
3) из $$\bigtriangleup GBH: BR=\frac{BG*BH}{GH}=$$$$\frac{5*3\sqrt{2}}{\sqrt{5^{2}+9*2}}=$$$$\frac{30}{\sqrt{86}}$$
Задание 4914
Основанием четырехугольной пирамиды SABCD является квадрат ABCD со стороной АВ=4. Боковое ребро SC, равное 4, перпендикулярно основанию пирамиды. Плоскость $$\alpha$$, проходящая через вершину С параллельно прямой BD, пересекает ребро SA в точке М, причем SM:MA=1:2
a) 1) $$AS=\sqrt{16+32}=4\sqrt{3}$$; $$AM=\frac{4\sqrt{3}\cdot2}{3}$$; $$MS=\frac{4\sqrt{3}}{3}$$; $$MC=\frac{4\cdot4\sqrt{2}}{4\sqrt{3}}=\frac{4\sqrt{2}}{\sqrt{3}}=\frac{4\sqrt{6}}{3}$$; $$4^{2}=(\frac{4\sqrt{6}}{3})^{2}+(\frac{4\sqrt{3}}{3})^{2}=\frac{16\cdot6+16\cdot3}{9}=16$$
2) $$AC\perp DB$$ $$\Rightarrow$$ $$SA\perp DB$$ $$\Rightarrow$$ $$SA\perp KN$$
б) 1) $$\frac{CE}{EM}\cdot\frac{MS}{SA}\cdot\frac{AO}{OC}=1$$; $$\frac{CE}{EM}\cdot\frac{1}{3}\cdot\frac{1}{1}=1$$; $$\frac{CE}{EM}=\frac{3}{1}$$ $$\Rightarrow$$ $$CE=\frac{3}{4}\cdot CM=\frac{3}{4}\cdot\frac{4\sqrt{6}}{3}=\sqrt{6}$$
2) $$\cos ACM=\frac{CM}{AC}=\frac{\frac{4\sqrt{6}}{3}}{4\sqrt{2}}=\frac{\sqrt{3}}{3}$$; $$OE=\sqrt{OC^{2}+CE^{2}-2OC\cdot CE\cdot\cos ACM}=$$ $$\sqrt{(2\sqrt{2})^{2}+(\sqrt{6})^{2}-2\cdot2\sqrt{2}\cdot\sqrt{6}\cdot\frac{\sqrt{3}}{3}}=$$ $$\sqrt{8+6-\frac{4\cdot6}{3}}=\sqrt{6}$$
3) $$SO=\sqrt{OC^{2}+SC^{2}}=\sqrt{(2\sqrt{2})^{2}+4^{2}}=\sqrt{24}$$ $$\Rightarrow$$ $$SE=SO-OE=2\sqrt{6}-\sqrt{6}=\sqrt{6}$$ $$\Rightarrow$$ $$NK$$ - средняя линия $$\bigtriangleup SDB$$ $$\Rightarrow$$ $$NK=\frac{1}{2}DB=\frac{1}{2}\cdot4\sqrt{2}=2\sqrt{2}$$;
4) $$S_{CKMN}=\frac{1}{2}\cdot CM\cdot NK=\frac{1}{2}\cdot\frac{4\sqrt{6}}{3}\cdot2\sqrt{2}=\frac{4\cdot\sqrt{12}}{3}=\frac{8\sqrt{3}}{3}$$
Задание 4961
В основании треугольной пирамиды ABCD лежит треугольник АВС, где АВ=ВС=5, АС=6. Боковые ребра наклонены к плоскости основания под углом, синус которого равен $$\frac{3}{4}$$.
Задание 5009
В основании прямой призмы $$ABCDA_{1}B_{1}C_{1}D_{1}$$ лежит прямоугольная трапеция АВСD с основаниями ВС и АD (ВС < АD), в которой АВ=5, CD=4, ВС=6. Через точку С и середину ребра $$BB_{1}$$ параллельно $$B_{1}D$$ проведена плоскость β.
Задание 5057
В основании прямой призмы $$ABCDA_{1}B_{1}C_{1}D_{1}$$ лежит ромб ABCD, причем AB=BD. Точки М и N – середины ребер $$B_{1}C_{1}$$ и АВ соответственно.
А) 1) Построение сечения: $$D_{1}M\cap A_{1}B_{1}=Q$$; $$QN\cap BB_{1}=T$$; $$QN\cap AA_{1}=G$$; $$GD_{1}\cap AD=K$$, тогда $$D_{1}MTNK$$ - сечение .
2) Так как $$AB=BD$$, то $$\Delta BDC$$ - равносторонний и $$\angle BDC=60$$. $$M_{1}$$ - середина BC (проекция M на (ABC))$$\Rightarrow$$ $$DM_{1}$$ - биссектриса $$\Delta BDC$$ и $$\angle BDM_{1}=30$$.Тогда $$\angle ADM_{1}=90$$, т.е. $$AD\perp DM_{1}$$, KD - проекция $$KD_{1}$$ на (ABC): $$KD\perp DM_{1}\Rightarrow$$ $$KD_{1}\perp DM_{1}$$ по т. Трех препендикулярах. Но $$D_{1}M\left | \right |DM_{1}$$ $$\Rightarrow$$ $$KD_{1}\perp D_{1}M$$ т.е. $$\angle KD_{1}M=90$$
Б) 1) Пусть площадь сечения $$S_{1}$$, а площадь его проекции $$S_{2}$$: $$S_{1}=\frac{S_{2}}{\cos \varphi }$$, где $$DKNBM_{1}$$ - проекция сечения, а $$\angle D_{1}KD=\varphi$$ – угол между плоскостью сечении яи основанием призмы , т.к. $$D_{1}K\perp KN, DK\perp KN$$.
2) Проведем $$BP\left | \right |M_{1}D$$. Тогда $$BM_{1}DP$$ - прямоугольник , $$M_{1}B=4$$; $$D_{1}M=DC \sin 60=4\sqrt{3}$$; $$S_{BM_{1}DP}=16\sqrt{3}$$; KPBN-прямоугольная трапеция ;$$BP=M_{1}D=4\sqrt{3}$$; $$KN=\frac{1}{2}BP=2\sqrt{3}$$ (т.к. N- середина AB); $$KP=\frac{1}{4}AD=2$$;
3) $$S_{KPBN}=\frac{4\sqrt{3}+2\sqrt{3}}{2}*2=6\sqrt{3}$$; $$S_{2}=16\sqrt{3}+6\sqrt{3}=22\sqrt{3};$$ $$KD_{1}=\sqrt{KD^{2}+DD_{1}^{2}}=\sqrt{6^{2}+(3\sqrt{2})^{2}}=3\sqrt{6};$$ $$\cos \varphi =\frac{KD}{KD_{1}}=\frac{6}{3\sqrt{6}}=\frac{2}{\sqrt{6}};$$ $$S_{1}=22\sqrt{3}:\frac{2}{\sqrt{6}}=33\sqrt{2};$$
Задание 5141
В прямоугольном параллелепипеде $$ABCDA_{1}B_{1}C_{1}D_{1}$$ $$AB=5$$, $$AD=6$$, $$AA_{1}=8$$ точка К – середина ребра $$DD_{1}$$
а) т.к. $$ABCDA_{1}B_{1}C_{1}D_{1}$$ - прямоугол. параллелипипед, то $$BC\perp(CC_{1}D_{1}D)$$, по $$KC_{1}\in(CC_{1}D_{1}D)$$ $$\Rightarrow$$ $$BC\perp KC_{1}$$
б) 1) $$BC_{1}$$ соединяем; $$KC_{1}$$ соединяем; $$(BCC_{1})\parallel(ADD_{1})$$ $$\Rightarrow$$ через К пройдет прямая параллельная прямая $$BC_{1}$$ $$\Rightarrow$$ $$KM$$; из подобия $$\bigtriangleup MKD$$ $$\bigtriangleup BC_{1}C$$; М - середина AD $$\Rightarrow$$ $$(BCKD)$$ - искомая плоскость
2) $$BCC_{1}MDK$$ - усеченная пирамида: $$V=\frac{1}{3}h(S_{1}+S_{2}+\sqrt{S_{1}S_{2}})$$; $$V_{1}=\frac{1}{3}DC\cdot(S_{BCC_{1}}+S_{MDK}+\sqrt{S_{BCC_{1}}\cdot S_{MDK}})$$; $$V_{1}=\frac{1}{3}\cdot5\cdot(\frac{1}{2}\cdot6\cdot8+\frac{1}{2}\cdot3\cdot4+\sqrt{\frac{1}{2}\cdot6\cdot8\frac{1}{2}\cdot3\cdot4})=$$ $$\frac{5}{3}(24+6+\frac{1}{2}\cdot3\cdot2)=\frac{5}{3}(30+12)=70$$
3) $$V_{ABCDA_{1}B_{1}C_{1}D_{1}}=5\cdot6\cdot8=240$$ $$\Rightarrow$$ объем оставшейся
$$V_{2}=240-70=170$$
4) $$\frac{V_{1}}{V_{2}}=\frac{70}{170}=\frac{7}{17}$$
Задание 5194
В правильной шестиугольной призме $$ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}$$ стороны основания равны 4, а боковые ребра 5.
a) 1) $$A_{1}$$ и $$C_{1}$$ соединяем . Пусть $$A_{1} C_{1} \cap E_{1} F_{1}=K$$, тогда E и K соединяем; $$EK\cap FD_{1}=M$$
Пусть $$A_{1} C_{1} \cap E_{1} F_{1}=R\Rightarrow ER\cap FF_{1}=N\Rightarrow (A_{1}NEMC_{1})$$- искомая $$(A_{1}C_{1}E)$$
2) $$E_{1}B_{1}\cap A_{1}C_{1}=H\Rightarrow EH$$-линия пересечения $$(A_{1}C_{1}E)$$ и $$(BB_{1}E_{1}E)$$
3) $$A_{1}C_{1}\perp E_{1}B_{1}$$(т.к. в основании правильной призмы) ,но $$A_{1}C_{1}\perp BB_{1}$$( т.к. призма правильная) $$\Rightarrow (A_{1}C_{1}E)\perp (BB_{1}E_{1}E)$$
b) 1)Отпустим $$HH_{1}\perp (ABCDEF)\Rightarrow HH_{1}=AA_{1}=5$$
2)Пусть O-центр основания $$\Rightarrow OE=AB=4$$
3) AOCB- ромб (OC=BC=AB=AO; $$\angle AOC=\angle ABC$$)$$\Rightarrow OH_{1}-H_{1}B=\frac{1}{2}OB=2$$
4) $$tg \angle HEH_{1}=\frac{HH_{1}}{EH_{1}}=\frac{5}{6}\Rightarrow \angle HEH_{1}-arctg\frac{5}{6}$$
Задание 5241
Дан куб $$ABCDA_{1}B_{1}C_{1}D_{1}$$. Пусть $$l$$ – линия пересечения плоскостей $$ACD_{1}$$ и $$BDC_{1}$$
A) введем систему координат. Пусть ребро куба 2. Тогда :$$H(1;1;0), M(1;0;1), D(0;0;0), B_{1}(2;2;2)$$
$$\vec{HM} (0;-1;1)$$; $$\vec{DB_{1}} (2;2;2)$$
$$\cos (HM; BD)=\frac{10*2+(-1)*2+1*2}{\sqrt{2}*\sqrt{12}}=0\Rightarrow$$ угол равен 90
Б) Построим из H прямую $$HK\left | \right | DB_{1}$$$$\Rightarrow \Delta DB_{1}B\sim \Delta HKB$$; H-середина DB, то и K-середина
$$BB_{1}\Rightarrow K(2;2;1)$$
Зададим уравнение (HKM):
$$\left\{\begin{matrix}a+b+d-0\\a+c+d=0 \\2a+ab+c+d=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}b=c \\a+c+d=0 \\2a+3c+d=0\end{matrix}\right.$$$$\left\{\begin{matrix}a=-c-d \\-2c-2d+3c+d=0 \\b=c \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}c=d \\b=c \\a=-2c\end{matrix}\right.$$
Получим: $$-2cx+cy+cz+c=0|:c \Leftrightarrow$$$$-2x+y+z+1=0$$
Найдем расстояние от D до (HKM)
$$r=\frac{\left | -2*0+1*0+1*0+1 \right |}{\sqrt{4+1+1}}=\frac{1}{\sqrt{6}}$$
Задание 5289
В конусе с вершиной в точке Р высота $$PO=\sqrt{7}$$. В его основании проведена хорда АВ, отстоящая от точки О на расстоянии, равном 3. Известно, что радиус основания конуса равен 5.
А) 1) Пусть $$(PC)\perp (AB)$$, $$c \in (AB)$$, тогда по теореме о 3-х перпендикулярах: $$(OC)\perp (AB)$$, $$\left | OC \right |=3$$
2) Из $$\Delta OPC:\left | PC \right |=\sqrt{\left | PO \right |^{2}+\left | OC \right |^{2}}=4$$
3) С другой стороны : $$\left | AB \right |=2\left | BC \right |=8=2\left | PC \right |$$ ($$\Delta BOC$$ - равнобедренный, соедовательно, высота является еще и медианой)
Б) 1) Пусть Q-центр сферы, описанной около пирамиды POAB . Тогда , в силу симметрии, $$Q \in (OPC)$$. Пусть $$D \in (OP)$$, $$\left | PD \right |=\left | DO \right |$$, тогда $$\left | OQ \right |:{2} (QD)\perp (PO)$$ . Так как $$(AB)\perp (OCP)$$ и $$\left | CB \right |=\left | AC \right |$$, то $$(OD)\left | \right |(CO)$$
2) Рассмотрим систему координат :O- начало, ось Oz-вдоль [OP], (Ox) вдоль [OC), $$(Oy)\left | \right |[BA)$$. Тогда :
$$Q=(x;0;\frac{\sqrt{7}}{2})$$;$$O=(0;0;0)$$;$$A=(3;4;0)$$
Отсюда: $$x^{2}+\frac{7}{4}=R^{2}=(x-3)^{2}+4^{2}+\frac{7}{4}\Leftrightarrow$$ $$(x-x+3)(2x-3)=16\Leftrightarrow$$ $$x=\frac{25}{6}\Rightarrow$$ $$R^{2}=\frac{625}{36}+\frac{7}{4}=$$$$\frac{172}{9}\Rightarrow$$ $$R=\frac{2}{3}\sqrt{43}$$
Задание 5337
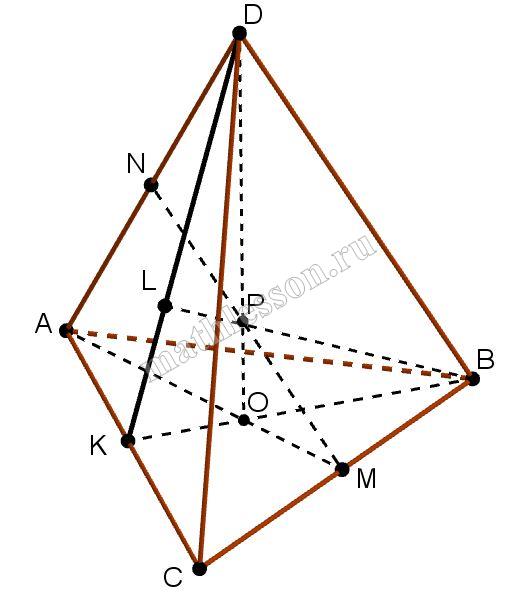
В треугольной пирамиде ABCD длины всех рёбер равны. Точка Р равноудалена от вершин А и D, причём известно, что PB = PC и прямая РВ перпендикулярна высоте треугольника АСD, опущенной из вершины D.
а) 1)PA=PD, тогда NP - серединный перпендикуляр для AD
2)PB = PC, тогда MP - серединный перпендикуляр для CB.
3)AM перпендикулярно CB, тогда NM также перпендикулярно CB и значит $$P \in NM ; P \in AMD$$
4)$$PB \cap DK = L$$. $$BK \perp AC \Leftrightarrow BL \perp AC$$, но по условию $$BL \perp DL$$, значит $$BL \perp (ADC)$$, то есть BL - высота пирамиды и $$P \in DKB$$. Следовательно, точка P лежит в двух плоскостях, значит принадлежит линии пересечения. $$(AMD) \cap (DKB) = PO$$, где PO - высота пирамиды, следовательно P лежит на пересечении высот
б)1) Пусть длина ребра х, тогда из треугольника ADC: $$DK=KB=\frac{\sqrt{3}x}{2}$$, $$DL=\frac{2}{3}DK=\frac{x\sqrt{3}}{3}$$ (по свойству медиан)
2)$$\sin LBD = \frac{DL}{DB}=\frac{\sqrt{3}}{3}$$, тогда $$\cos LBD = \frac{\sqrt{6}}{3}$$ ( по основному тригонометрическому тождеству )
3)из треугольника PQB: $$QB=PB \cos LBD $$, $$QB=\frac{1}{2}x$$ (свойство медианы). Тогда $$\frac{1}{2}x=\frac{\sqrt{3}}{2}*\frac{\sqrt{6}}{3}=1$$, тогда ребро равно 2
4)Из треугольника ABC :$$BK=\frac{\sqrt{3}}{2}*2=\sqrt{3}$$, $$OB = \frac{2}{3}BK = \frac{2\sqrt{3}}{3}$$
5)$$DO=\sqrt{DB^{2}-OB^{2}}=\sqrt{\frac{8}{3}}$$, тогда $$S_{ABC}=\frac{1}{2}*2*2*\frac{\sqrt{3}}{2}=\sqrt{3}$$, и объем пирамиды $$V=\frac{1}{3}S_{ABC}*DO=\frac{1}{3}*\sqrt{3}*\frac{\sqrt{8}}{\sqrt{3}}=\frac{\sqrt{8}}{3}$$