ЕГЭ (профиль) / Наибольшее и наименьшее значение функций

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$y=log_{3}(x^{2}-6x+10)+2$$ Найдем минимальное значение функции; $$y_{min}$$ при $$x^{2}-6x+10\rightarrow min$$ Минимальное значение квадратичная функция принимает в вершине параболы (ветви вверх): $$x_{0}=-\frac{-6}{2}=3\Rightarrow$$ $$y_{0}=9-6*3+10=1$$ Тогда минимальное значение функции: $$y_{min}=log_{3}(1)+2=2$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Воспользуемся неравенством: $$\left | \bar{a} \right |+\left | \bar{b} \right |\geq \left | \bar{a}+\bar{b} \right |$$ Рассмотрим правило треугольника : $$AB=\left | \bar{a} \right |; BC=\left | \bar{b} \right |; AC=\left | \bar{a}+\bar{b} \right |$$. По свойству треугольника: $$AC\leq AB+BC$$ При этом Знак равно $$(\left | \bar{a} \right |+\left | \bar{b} \right |=\left | \bar{a}+\bar{b}\right |)$$ только тогда, когда $$\bar{a}$$ и $$\bar{b}$$ сонаправлены , т.е. когда $$\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}$$ (где $$\bar{a}(x;y));\bar{b}(x_{2};y_{2})$$) Выделим полные квадраты под корнями: $$x^{2}-2x+2=x^{2}-2x+1+1=(x-1)^{2}+1$$ $$x^{2}-10x+29=x^{2}-10x+25+4=(x-5)^{2}+4$$ Найдем наименьшее значение: $$y=\sqrt{(x-1)^{2}+1}+\sqrt{(x-5)^{2}+4}$$ Пусть: $$\bar{a}=(1-x; 1); \bar{b}(x-5; 2)$$ (Если найти длины векторов, получим подкоренные выражения) Тогда: $$\left | \bar{a} \right |=\sqrt{(1-x)^{2}+1}=\sqrt{(x-1)^{2}+1}$$ и $$\left | \bar{b} \right |=\sqrt{(x-5)^{2}+4}$$ Каждая координата суммарного вектора, равна сумме соответствующих координат первоначальных векторов: $$\bar{a}+\bar{b} =(1-x+x-5, 1+2)=(-4 ;3)$$ Тогда его длина: $$\left | \bar{a}+\bar{b} \right |=\sqrt{(-4)^{2}+3^{2}}=5$$ В таком случае получаем: $$\left | \bar{a} \right |+\left | \bar{b} \right |\geq \left | \bar{a}+\bar{b} \right |, y(x)\geq 5$$ То есть минимальное значение данной функции равно 5.

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

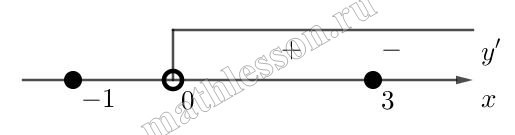
$${y}'=\frac{1}{2\sqrt{2\lg x-1}}*\frac{2}{x\ln 10}-\frac{1}{x\ln10}=0$$

$$\frac{1}{x\ln 10}(\frac{1}{2\sqrt{2\lg x-1}})=0$$

$$\left\{\begin{matrix}x\neq 0 \\\sqrt{2\lg x-1}=1(1)\end{matrix}\right.$$

$$(1): \sqrt{2\lg x-1}=1\Leftrightarrow$$ $$2\lg x-1\leq 1\Leftrightarrow$$ $$2\lg x=2\Leftrightarrow$$ $$\lg x=1\Leftrightarrow x=10$$

$$y(10)=y=\sqrt{2\lg 10-1}-\lg 10=1-1=0$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     При x>0: $$\sqrt{4x^{4}=3x^{2}+9}>\sqrt{4x^{4}-8x^{2}+9}$$

     Пусть $$t=\frac{\sqrt{4x^{4}-3x^{2}+9}-\sqrt{4x^{4}-8x^{2}+9}}{x}=$$$$\frac{4x^{4}-3x^{2}+9-(4x^{4}-8x^{2}+9)}{x(\sqrt{4x^{4}-3x^{2}+9}+\sqrt{4x^{4}-8x^{2}+9})}=$$$$\frac{5x^{2}}{\sqrt{4x^{4}-3x^{2}+9}+\sqrt{4x^{4}-8x^{2}+9}}=$$$$\frac{5}{\sqrt{4x^{4}-\frac{9}{x^{2}}-3}+\sqrt{4x^{4}-\frac{9}{x^{2}}-8}}$$

     Учтем, что $$a^{2}+b^{2}\geq 2ab$$. Пусть $$a^{2}=4x^{2}, b^{2}=\frac{9}{x^{2}}$$. Тогда: $$4x^{2}+\frac{9}{x^{2}}\geq 2\sqrt{4x^{2}*\frac{9}{x^{2}}}=2*6=12(1)$$

     Следовательно $$\sqrt{4x^{4}-\frac{9}{x^{2}}-3}+\sqrt{4x^{4}-\frac{9}{x^{2}}-8}(2)$$ минимальна при выполнении (1):

$$\sqrt{12-3}+\sqrt{12-8}=3+2=5$$. Чем меньше (2), тем больше t и тем меньше: $$\log_{0,5}t\Rightarrow \log_{0,5}\frac{5}{5}=\log_{0,5}1=0$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

На промежутке [1;6] x+5>0 4x-3>0, тогда: $$y=7\left | x-3 \right |-2x-10-4x+3+5=$$$$7\left | x-3 \right |-6x-2$$

Вершина полученного графика будет находиться в точке, где подмодульное выражение равно 0, то есть $$x=3\Rightarrow$$ $$y_{min}=y(3)$$

$$y(3)=7\left | 3-3 \right |-6*3-2=-20$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Пусть $$\bar{a}: (2x-1; 3y-1);\bar{b}: (3y-2x ; -3y)$$

     Из неравенства $$\left | \bar{a} \right |+\left | \bar{b} \right |\geq \left | \bar{a}+\bar{b} \right |$$, и учитывая , что $$\bar{a}+\bar{b}:(2x-1+3y-2x;3y-1-3y)=(3y-1;-1)$$, и $$z=\left | \bar{a} \right |+\left | \bar{b} \right |$$ получим : $$z\geq \left | \bar{a}+\bar{b} \right |=\sqrt{(3y-1)^{2}+(-1)^{2}}$$

     Рассмотрим $$(3y-1)^{2}+(-1)^{2}=g$$ .Т.к. $$(3y-1)^{2}\geq 0$$ при любом y,  $$g\rightarrow min$$, только тогда, когда $$3y-1\rightarrow 0$$, следовательно, $$g_{min}=1$$. Т.е. $$z\geq \sqrt{1}=1$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Так как дан логарифм, то будет ОДЗ: $$x>0$$

     Найдем производную данной функции: $${y}'=\frac{6}{x}-2(x-2)$$

     Приравняем производную к нулю: $$\frac{6-2x^{2}+4x}{x}=0$$

$$2x^{2}-4x+6=0\Leftrightarrow$$$$x^{2}-2x+3=0\Leftrightarrow$$$$(x-3)(x+1)=0$$

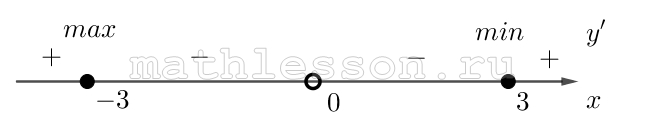
     Тогда производная имеет вид: $${y}'=\frac{-2(x-3)(x+1)}{x}$$. При этом, с учетом ОДЗ и знаков производной на полученных промежутках ((0;3) и $$(3;\infty)$$) получим, что $$x(3)=x_{max}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Найдем производную и приравняем ее к нулю: $$f'(x)=3x^{2}-6x-9=0\Leftrightarrow$$$$x^{2}-2x-3=0\Leftrightarrow$$$$\left\{\begin{matrix}x_{1}+x_{2}=2\\x_{1}*x_{2}=-3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=3\\x_{2}=-1\end{matrix}\right.$$

     При этом х=3 - является точкой минимума (х=-1 - точка максимума). Тогда минимальное значение функции: $$f_{min}=f(3)=3^{3}-3*3^{2}-9*3+31=4$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$y'=\cos x+9$$ . Т.к. $$\left | \cos x \right |\leq 1$$, то $$\cos x+9>0$$, при всех x. Тогда функция возрастает на всем промежутке и $$y_{max}=y(0)$$: $$y(0)=\sin 0+9*0-9=-9$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Функция $$f(x)=2^{x}$$ - возрастает, $$g(x)=3^{x}$$ - возрастает, тогда $$m(x)=2^{x}+3^{x}$$ - возрастает на всем промежутке, тогда $$y=\frac{40}{2^{x}+3^{x}}$$ - убывает. Следовательно, $$y_{max}=y(1)=\frac{40}{2+3}=8$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Найдем производную для $$y=2,7*e^{3x^{2}-x^{3}-4}$$: $${y}'=2,7*e^{3x^{2}-x^{2}-4}*{(3x^{2}-x^{3}-4)}'=$$$$2,7*e^{3x^{2}-x^{3}-4}*(6x-3x^{2})$$

Приравняем производную к 0: $${y}'=0\Leftrightarrow$$ $$6x-3x^{2}=0\Leftrightarrow$$ $$3x(2-x)=0\Leftrightarrow$$$$\left[\begin{matrix}x=0\\x=2\end{matrix}\right.$$. x=0 - точка минимума, x=2 - максимума

$$f_{max}=f(2)=2,7*e^{3*2^{2}-2^{3}-4}=2,7$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Найдем производную : $${y}'=12 \cos x-6\sqrt{3}$$

Приравняем к 0: $$12 \cos x=6\sqrt{3}\Leftrightarrow$$ $$\cos x=\frac{\sqrt{3}}{2}\Leftrightarrow$$ $$\pm \frac{\pi}{6}+2 \pi n , n \in Z$$

Как видим $$\frac{\pi}{6}$$ - точка максимума, тогда: 

$$y_{max}=y(\frac{\pi}{6})=$$$$12 *\frac{1}{2}-6\sqrt{3}*\frac{\pi}{6}+\sqrt{3} \pi +6 =12$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$y=\frac{x^{3}+x^{2}+9}{x}-x^{2}=\frac{x^{3}+x^{2}+9-x^{3}}{x}=\frac{x^{2}+9}{x}$$

$${y}'=\frac{{(x^{2}+9)}'x-(x^{2}+9)*{x}'}{x^{2}}=\frac{2x^{2}-x^{2}-9}{x^{2}}=\frac{x^{2}-9}{x^{2}}=0$$

$$\left\{\begin{matrix}x^{2}-9=0\\x^{2}\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\pm 3\\x\neq 0\end{matrix}\right.$$

$$f(-3)=\frac{(-3)^{2}+9}{(-3)}=-6$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Раскроем модули :

1) $$x \in (-\infty ;-1]\Rightarrow$$ $$y=x^{2}-x-x-1=x^{2}-2x-1$$

2) $$x \in (-1,0]\cup [1;+\infty )\Rightarrow$$ $$y=x^{2}-x+x+1=x^{2}+1$$

3) $$x \in (0;1)\Rightarrow$$ $$y=-x^{2}+x+x+1=-x^{2}+2x+1$$

Следовательно , $$y _{min}=1$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

          Пусть $$7^{5x}=m>0$$, тогда: $$f(m)=\frac{m}{7^{2}}+\frac{9*7^{4}}{m}-41$$

          Найдем производную данной функции: $${f}'(m)=\frac{1}{7^{2}}-\frac{9*7^{4}}{m^{2}}=0$$$$\Leftrightarrow$$ $$\frac{m^{2}-9*7^{6}}{(7m)^{2}}=0$$$$\Leftrightarrow$$$$m=\pm 3*7^{3}$$

          Так как $$m>0$$ $$\Rightarrow$$ $$m=7^{5x}=3*7^{3}$$ - при данном значении и будет наименьшее значение функции:

          $$y=\frac{3*7^{3}}{7^{2}}+\frac{9*7^{4}}{3*7^{3}}-41=42-41=1$$