ОГЭ
Задание 6072
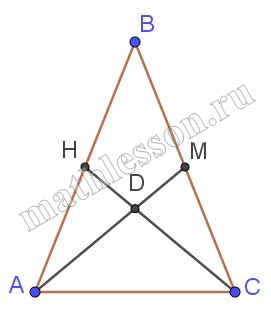
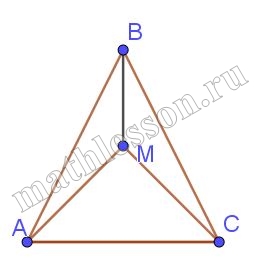
Докажите, что если у треугольника равны две медианы, то этот треугольник равнобедренный.
1) Пусть АМ=СН-медианы . $$\frac{LN}{LM}=\frac{2}{1}$$ и $$\frac{CL}{CH}=\frac{2}{1}$$(свойство медиан), но т.к. AM=CH, то AL=LC ,LH=LM.
2) $$\angle HLA=\angle MLC$$ (вертикальные) $$\Delta HLA=\Delta MLC$$ (по 2-м сторонам и углу между ними) $$\Rightarrow$$ AH=MC, но AH=HB и CM=MB $$\Rightarrow$$ AB=BC.
Задание 6119
Середины сторон параллелограмма являются вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
- $$AB=CD, BC=AD$$ так как дан параллелограмм. Следовательно, $$AM=MB=DL=LC$$, и $$AK=KD=BN=NC$$.
- $$\angle A+\angle D=180$$. Но $$MK=NK$$, следовательно, треугольники AMK и KLD равны по трем сторонам и $$\angle A=\angle D$$. Так как они в сумме дают 180, то какждый из них по 90, тогда ABCD - прямоугольник.
Задание 6166
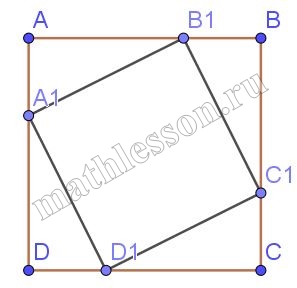
В квадрат, площадью 24 см2 вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон прямоугольника относятся как 1:3. Найдите площадь прямоугольника.
1) Пусть $$\angle B_{1}C_{1}B=\alpha$$ , тогда $$\angle D_{1}C_{1}C=90-\alpha$$ , тогда $$\angle C_{1}D_{1}C=\alpha$$ .
Рассуждая аналогично получим :
$$\angle B_{1}C_{1}B=\angle C_{1}D_{1}C =\angle DA_{1}D_{1}=\angle A_{1}B_{1}A=\alpha$$ , следовательно , $$\angle B_{1}C_{1}B\sim \angle C_{1}D_{1}C \sim \angle DA_{1}D_{1}\sim \angle A_{1}B_{1}A$$
2)т.к. $$B_{1}C_{1}:C_{1}D_{1}=1:3$$,то пусть $$B_{1}B=x\Rightarrow CC_{1}=3x, BC_{1}=y$$, тогда $$CD_{1}=3y.$$
3) т.к. $$A_{1}B_{1}=C_{1}D_{1}$$ и $$B_{1}C_{1}=A_{1}D_{1}$$ и все треугольники подобны , то $$\Delta A_{1}B_{1}A=\Delta C_{1}D_{1}C$$ и $$\Delta B_{1}C_{1}B=\Delta DA_{1}D_{1}$$ следовательно $$DD_{1}=x$$
4) из п. 3 получили, что $$BC=y+3x$$ и $$CD=x+3y$$, тогда
$$y+3x=x+3y\Rightarrow x=y$$
5)$$AC=\sqrt{S_{ABCD}}=\sqrt{24}$$
$$\frac{BC_{1}}{CC_{1}}=\frac{1}{3}\Rightarrow$$$$ BC_{1}=\frac{\sqrt{24}}{4}\Rightarrow$$$$CC_{1}=\frac{3\sqrt{24}}{4}$$
6) $$\Delta B_{1}BC_{1}$$: $$B_{1}C_{1}=\sqrt{(\frac{\sqrt{24}}{4})^{2}+(\frac{\sqrt{24}}{4})^{2}}=\sqrt{3}.$$Тогда $$C_{1}D_{1}=3\sqrt{3}.$$
7)$$S_{A_{1}B_{1}C_{1}D_{1}}=3\sqrt{3}*\sqrt{3}=9$$
Задание 6167
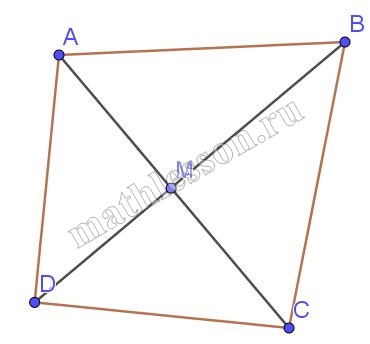
В выпуклом четырёхугольнике АВСD углы ACB и ADB равны. Докажите, что углы ABD и ACD также равны.
1) $$\angle AMD=\angle BMC$$(вертикальные) $$\angle ADB=\angle ACB$$(по условию) $$\Rightarrow \Delta AMB \sim \Delta BMC$$ и $$\frac{AM}{MB}=\frac{MD}{MC}(1)$$
2) $$\angle AMB=\angle DMC$$ (вертикальные) с учетом равенства (1) получим $$\Delta AMB \sim \Delta DMC\Rightarrow \angle ABD=\angle ACD$$
Задание 6214
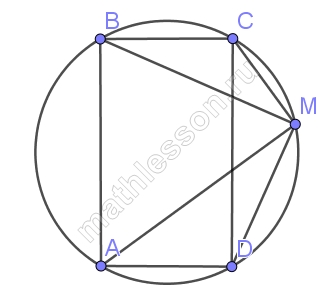
Точка М лежит на окружности радиуса R, описанной около прямоугольника ABCD. Докажите, что МА2 + МВ2 + МС2 + МD2 = 8R2
- $$\angle CMA=90$$, AC-диаметр окружности . Тогда из $$\Delta ACM$$
- $$AC^{2}=MC^{2}+MA^{2}\Leftrightarrow (2R)^{2}=MC^{2}+MA^{2}(1)$$
- Аналогично , из $$\Delta BMD: (2R)^{2}=MB^{2}+MD^{2}(2)$$
- Сложим (1)и(2): $$MA^{2}+MB^{2}+MC^{2}+MD^{2}=8R^{2}$$
Задание 6262
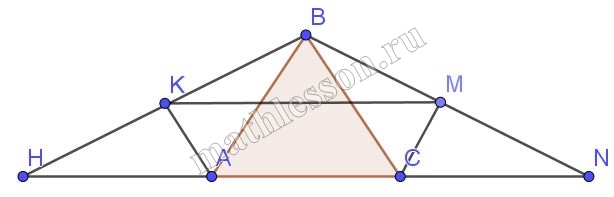
Из вершины В треугольника АВС опущены перпендикуляры ВК и ВМ на биссектрисы внешних углов треугольника, не смежных с углом В. Докажите, что длина отрезка КМ равна полупериметру треугольника АВС.
1) $$BK\cap AC=H; BM\cap AC=N$$
Из $$\Delta HAB$$: AK-высота и биссектриса $$\Rightarrow$$ и медиана и $$AH=AB$$ ($$\Delta AHB$$-равнобедренный)
Из $$\Delta BCH$$: аналогично CM-медиана и BC=CN
2) из п. 1 $$HN=HA+AC+CN=$$$$AB+AC+DC=P_{ABC}$$
K и M-середины , тогда KM-средняя линия и $$KM=\frac{1}{2}HN=\frac{P_{ABC}}{2}$$
Задание 6310
На основаниях АВ и СD вне трапеции построены квадраты. Докажите, что прямая, соединяющая их центры, проходит через точку пересечения диагоналей трапеции.
Пусть $$K\in B_{1}C$$, $$O=BD\cap AC$$, $$M=KO\cap AD$$
1) $$\angle LCK=\angle MAN=45$$; $$\angle LCO=\angle OAN$$(накрест лежащие) $$\Rightarrow \angle KCA=\angle OAD_{1}\Rightarrow$$ $$CB_{1}\left | \right |AD_{1}$$
2) $$\angle LKC=\angle NMA$$(накрест лежащие) $$\Rightarrow \Delta KLC\sim \Delta ANM\Rightarrow$$ $$\frac{KC}{AM}=\frac{CL}{AN}=k$$
3) $$LC\left | \right |AN\Rightarrow$$ $$\Delta LCO\sim \Delta ONA\Rightarrow$$ $$\frac{LC}{AN}=\frac{LO}{ON}=k$$
4) $$LC\left | \right |AN \Rightarrow$$ $$\Delta BLO\sim \Delta OND\Rightarrow$$ $$\frac{LO}{ON}=\frac{BL}{ND}=k$$
5)т.к. $$\frac{LC}{AN}=k$$, $$\frac{BL}{ND}=k$$ $$\Rightarrow \frac{BC}{AD}=k$$,но $$\frac{KC}{AM}=k$$ и $$\angle KCL=\angle MAN\Rightarrow$$ $$\Delta KCB\sim \Delta ADC$$ и если K-центр , то и М-центр
Задание 6357
Докажите, что в прямоугольном треугольнике произведение длин отрезков, на которые делит гипотенузу точка касания с вписанной окружностью, равна площади треугольника.

1) Пусть AH=x; HB=y; NO=OM=OH=r. По свойству касательных: AN=AH=x, MB=HB=y
2) $$S_{ABC}=\frac{1}{2}AC*CB=$$$$\frac{1}{2}(x+r)(y+r)=$$$$\frac{1}{2}xy+\frac{1}{2}xr+\frac{1}{2}yr+\frac{1}{2}r^{2}(1)$$
С другой стороны : $$S_{ABC}=2S_{AOH}+2S_{HOB}+S_{CNOM}=$$$$2S_{AOB}+S_{CNOM}=2*\frac{1}{2}(x+y)r+r^{2}=xr+yr+r^{2}(2)$$
Приравняем (1) и (2):
$$\frac{1}{2}xy+\frac{1}{2}xr+\frac{1}{2}yr+\frac{1}{2}r^{2}=xr+yx+r^{2}$$
$$\frac{1}{2}xy=\frac{1}{2}xr+\frac{1}{2}yr+\frac{1}{2}r^{2}|*2$$
$$xy=xr+y^{2}+r^{2}=S_{ABC}$$
Задание 6404
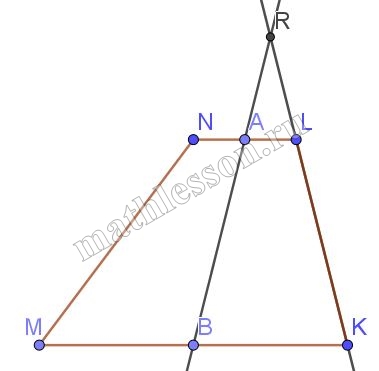
На одной из параллельных сторон трапеции взята точка А, на другой – точка В. Докажите, что отрезок АВ делится средней линией трапеции пополам.
1) Достроим $$BA\cap KL=R$$. $$\Delta ARL\sim \Delta RHH\sim \Delta BRK$$ ( т.к. $$AL\left | \right |HP\left | \right | BK$$)
2) По т. Фелеса : $$RL:LP:PK=AR: AH: HB \Rightarrow$$ $$LP :PK =1:1\Rightarrow AH: HB= 1 :1$$
Задание 6451
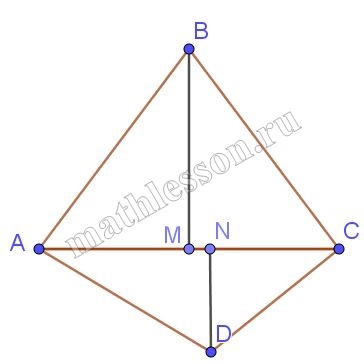
В выпуклом четырёхугольнике ABCD противоположные углы А и С прямые. На диагональ АС опущены перпендикуляры ВМ и DN. Докажите, что СМ = NA.
1) Пусть $$\angle ABM=\alpha$$, тогда из $$\Delta ABM: \angle BAM=90-\alpha$$ , тогда $$\angle MAD=\alpha$$ и из $$\Delta ADH:$$$$\angle ADN =90-\alpha \Rightarrow$$ $$\Delta ABM\sim \Delta AND$$, тогда : $$\frac{DH}{AM}=\frac{AN}{BM}\Rightarrow$$ $$DN*BM=AM*AN(1)$$
2) Аналогично $$\Delta BMC\sim \Delta CHD$$ и $$\frac{DH}{CM}=\frac{NC}{BM}\Rightarrow$$ $$DN*BM=CM*NC(2)$$
3) С учетом (1) и (2): $$AM *AN=CM*NC$$ или $$AM(AM+MN)=CN(CN+MN)\Leftrightarrow$$ $$AM^{2}+AM*MN=CN^{2}+CN*MN\Leftrightarrow$$ $$AM^{2}-CN^{2}+AM*MN-CN*MN=0\Leftrightarrow$$ $$(AM-CN)(AM+CN)+MN(AM-CN)=0\Leftrightarrow$$ $$(AM-CN)(AM+CN+MN)=0$$. $$AM+CN+MN>0$$ всегда, следовательно, $$AM-CN=0$$ или $$AM=CN$$
Задание 6506
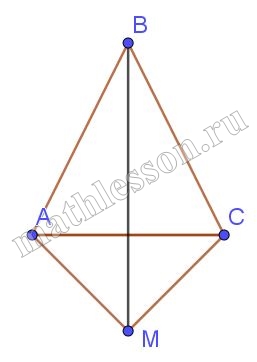
В равнобедренном треугольнике АВС из концов основания АС проведены прямые, которые составляют с основанием равные углы и пересекаются в точке М. Докажите равенство треугольников АВМ и ВСМ
Есть два случая расположения точки M:
1) $$\angle CAM =ACM \Rightarrow$$ $$\Delta ACM$$ –равнобедренный , тогда AM=MC
2) Треугольник ABC - ранвобедренный, следовательно, AB=BC.
3) BM - общая, следовательно, треугольники равны по трем сторонам.
Задание 6553
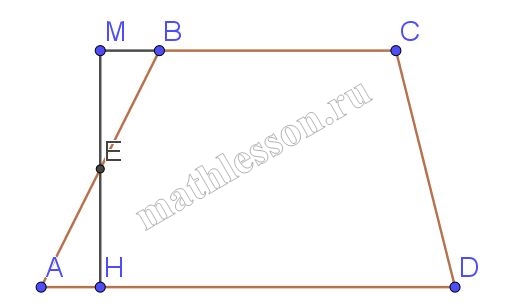
Биссектрисы углов А и D равнобедренной трапеции АВСD пересекаются в точке М стороны ВС. Докажите, что М – середина ВС.
1) $$\angle A=\angle D\Rightarrow$$ $$\angle BAM=\angle MDC$$
2) $$\angle BAM=\angle MAD$$(AM-биссектриса ); $$\angle MAD=\angle BMA$$(накрест лежащие) $$\Rightarrow \angle BAM=\angle BMA\Rightarrow$$ $$\Delta ABM$$ - равнобедренный
3)Аналогично $$\Delta MCD$$ - равнобедренный $$\Rightarrow$$ $$AB=BM; MC=CD$$, но $$AB=CD\Rightarrow BM=MO$$
Задание 6600
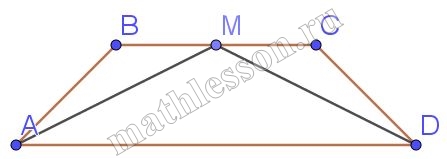
Пусть Е – середина стороны АВ трапеции АВСD (ВС ॥ АD). Докажите, что площадь треугольника ЕСD равна половине площади трапеции АВСD.
- Пусть $$EH\perp AD; EH=h$$
- $$\Delta EMD=\Delta EHA$$(по гипотенузе и острому углу )$$\Rightarrow$$ $$EM=h\Rightarrow$$ $$MH=2h$$
- Пусть $$BC=x; AD=y$$: $$S_{ABCD}=\frac{x+y}{2}*2h=xh+yh$$, $$S_{EBC}=\frac{1}{2}hx$$, $$S_{EAD}=\frac{1}{2}hy\Rightarrow$$ $$S_{CED}=h(x+y)-\frac{1}{2}h(x+y)=$$$$\frac{1}{2}h(x+y)=\frac{S_{ABCD}}{2}$$
Задание 6648
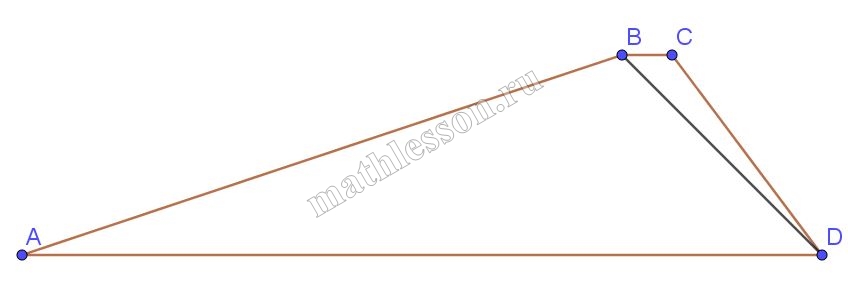
Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и BDA подобны.
1) $$\angle CBD=\angle BDA$$(накрест лежащие)
2) $$\frac{BD}{AD}=\frac{BC}{BD}$$. С учетом п.1 получим, что $$\Delta BCD\sim \Delta BDA$$
Задание 6715
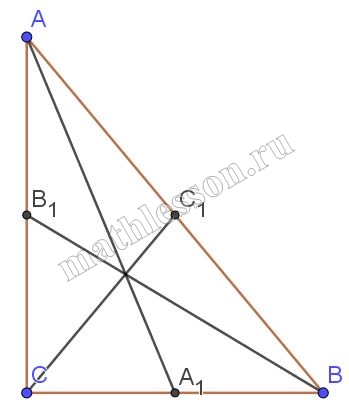
Докажите, что сумма квадратов медиан прямоугольного треугольника в 1,5 раза больше квадрата гипотенузы.
1) $$CC_{1}=\frac{1}{2}AB$$( свойство медиан из прямого угла) пусть $$AC^{2}=x^{2}$$, $$CB^{2}=y^{2}\Rightarrow$$ $$AB^{2}=x^{2}+y^{2}$$
2) $$CC_{1}^{2}=(\frac{AB}{2})^{2}=\frac{x^{2}+y^{2}}{4}$$
$$\Delta AA_{1}C$$: $$AA_{1}^{2}=AC^{2}+(\frac{CB}{2})^{2}=$$$$x^{2}+\frac{y^{2}}{4}$$
$$\Delta CBB_{1}$$: $$BB_{1}^{2}=CB^{2}+(\frac{AC}{2})^{2}=$$$$y^{2}+\frac{x^{2}}{4}$$
3) $$AA_{1}^{2}+BB_{1}^{2}+CC_{1}^{2}=$$$$x^{2}+\frac{y^{2}}{4}+y^{2}+\frac{x^{2}}{4}+\frac{x^{2}}{4}+\frac{y^{2}}{4}=$$$$\frac{3x^{2}+3y^{2}}{2}=1,5(x^{2}+y^{2})=1,5AB^{2}$$