ОГЭ
Задание 4536
На стороне ВС квадрата АВСD взята точка К. Докажите, что площадь треугольника АКD равна половине площади квадрата.
1) Пусть х - сторона квадрата, S - его площадь: $$S=x^{2}$$
2) Пусть $$KH\perp AD$$ $$\Rightarrow$$ $$KH=AB=x$$ $$\Rightarrow$$ $$S_{AKD}=\frac{1}{2}\cdot AD\cdot KH=\frac{1}{2}\cdot x\cdot x=\frac{x^{2}}{2}=\frac{S}{2}$$
ч.т.д.
Задание 4653
На медиане KF треугольника MKP отмечена точка E. Докажите, что если EM=EP, то KM=KP.
Построим чертеж:

Задание 4803
Докажите, что сумма длин медиан треугольника меньше его периметра
На каждой стороне треугольника достроим параллелограмм, как показано на рисунке и введем обозначения: BC=a;AB=c;AC=b;CC1=mc;BB1=mb;AA1=ma
Задание 4871
На высоте AD треугольника ABC взята точка N. Докажите, что AB2 - AC2 = NB2 - NC2 .
Задание 4898
Докажите, что биссектрисы углов прямоугольника с неравными сторонами при пересечении образуют квадрат.
1)$$\angle JAD = \angle JDA = 45^{\circ}$$ (AJ и DJ - биссектрисы пярмых углов), тогда $$\angle AJD = 90^{\circ}$$. Тогда $$\angle FJI =90^{\circ}$$ как смежный. Аналогично $$\angle FGI =90^{\circ}$$ и тогда FGIJ - прямоугольник
2)$$\bigtriangleup AJD = \bigtriangleup BGC$$ (прямоугольные, равнобедренные, одинаковые гипотенуза), тогда DJ=GC(1). $$\bigtriangleup DFC$$ прямоугольный и равнобедренный, тогда DF=FG(2). Из равенств 1 и 2 получаем FJ=FG. Тогда FGIJ - квадрат
Задание 4992
В четырехугольнике две стороны параллельны, а диагонали взаимно перпендикулярны. Докажите, что если в данный четырехугольник можно вписать окружность, то две другие стороны четырёхугольника равны между собой.
Задание 5041
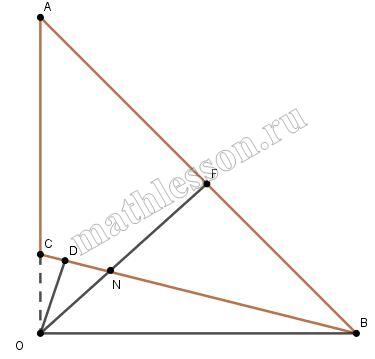
В треугольнике АВС угол АСВ тупой, $$BO\perp AC$$, $$OF\perp AB$$, $$OD\perp BC$$. Докажите, что $$\angle ACB=\angle DFB$$.
Пусть $$\angle A=\alpha$$; $$\angle B=\beta$$ $$\Rightarrow$$ $$\angle ACB=180-\angle\alpha-\angle\beta$$
1) $$\angle BCO=180-\angle C=\alpha+\beta$$ $$\Rightarrow$$ из $$\bigtriangleup OCB$$: $$\angle CBO=90^{\circ}-\angle BCO=90^{\circ}-\alpha-\beta$$
2) $$\bigtriangleup ODN\sim\bigtriangleup FNB$$ (прямоугольные); $$\angle DNO=\angle FNB$$ (как вертикал.); $$\Rightarrow$$ $$\frac{ON}{NB}=\frac{DN}{FN}$$ $$\Rightarrow$$ $$\frac{ON}{DN}=\frac{NB}{NF}$$ $$\Rightarrow$$ $$\angle DFN=\angle NBO=90^{\circ}-\alpha-\beta$$ $$\Rightarrow$$ $$\angle DFB=90^{\circ}+90^{\circ}-\alpha-\beta=180^{\circ}-\alpha-\beta=\angle ACB$$
ч.т.д.
Задание 5088
Докажите, что если в треугольнике два угла равны, то он равнобедренный.
Пусть $$BH\perp AC$$ $$\Rightarrow$$ $$\bigtriangleup ABH\sim\bigtriangleup BHC$$ по 2 углам, но т.к. $$BH$$ - общая ,то $$\bigtriangleup ABH=\bigtriangleup BHC$$ $$\Rightarrow$$ $$AB=BC$$
ч.т.д.
Задание 5225
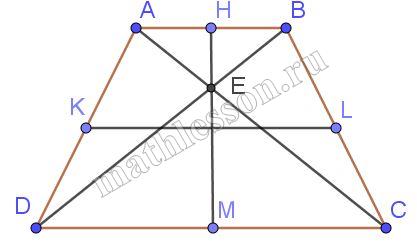
Докажите, что в трапеции, диагонали которой являются биссектрисами углов при одном из оснований, длины трёх сторон равны.
1)$$\angle BDA=\angle DBC$$(накрестлежащие при параллельных BC и AD) ; $$\angle BDA=\angle BDC$$ (BD - биссеткриса) , тогда $$\angle BDC=\angle DBC$$, тогда треугольник BDC - равнобедренный и BC=BD(1)
2)аналогично рассматривается равенство углов BAC и BCA, тогда треугольник ABC - равнобедренный, и AB=BC, но с учетом равенства (1) получаем AB=BC=CD.
ч.т.д.
Задание 5273
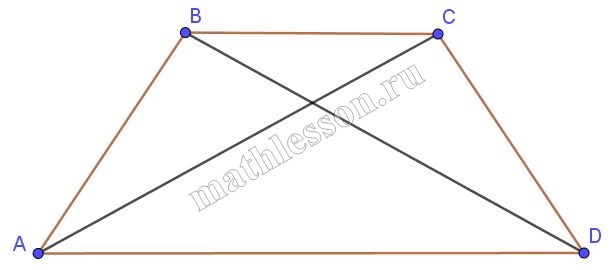
В выпуклом четырёхугольнике ABCD углы DAC и DBC равны. Докажите, что углы CDB и САВ также равны.
1) $$\angle CBD=\angle CAD$$ они опираются на $$CD$$ $$\Rightarrow$$ $$ABCD$$ можно вписать в окружность
2) $$\angle CDB$$ и $$\angle CAB$$ опираются на $$BC$$ и из пункта 1 получаем, что они вписанные $$\Rightarrow$$ т.к. на одну хорду опираются, то $$\angle CDB=\angle CAB$$
ч.т.д.
Задание 5321
На стороне BC квадрата ABCD взята точка М. Докажите, что площадь треугольника AМD равна половине площади квадрата.
1)Пусть $$MH \perp AD$$ , тогда ABMH - прямоугольник и MH=AB
2)$$S_{AMD}=\frac{1}{2}AD*MH$$, или $$S_{AMD}=\frac{1}{2}AD*AB=\frac{1}{2}S_{ABCD}$$
Задание 5368
Докажите, что если в равнобедренной трапеции диагонали взаимно перпендикулярны, то высота трапеции равна средней линии.
Задание 5416
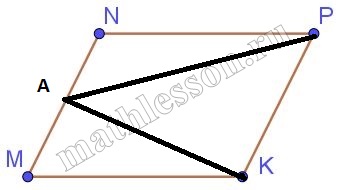
В параллелограмме MNPK точка A — середина стороны MN. Известно, что AP=AK. Докажите, что данный параллелограмм — прямоугольник.
1) По свойству параллелограмма: MN=NP. По условию AN=AM и AP=AK. Тогда треугольники ANP и AMK равны по трем сторонам, следовательно $$\angle ANP=\angle AMK=x$$
2) По свойству параллелограмма: $$\angle ANP+\angle AMK=180$$, следовательно $$\angle ANP=\angle AMK=90$$, тогда MNPK - прямоугольник