ОГЭ
Задание 7901
На плане изображено домохозяйство. При входе на участок справа от ворот находится баня, а слева – гараж, отмеченный цифрой 7. Площадь, занятая гаражом, равна 32 м2. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки. Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 м2, вымощенная такой же плиткой. К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
1. Найдите, на сколько метров периметр участка земли, занятого под жилой дом, больше периметра участка земли, занятого под сарай.
2. Тротуарная плитка продаётся в упаковках по 8 штук. Сколько упаковок понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
3. Найдите общую площадь (в м2) участка, которую занимают сарай и баня.
4. Найдите расстояние от теплицы до бани (расстояние между двумя ближайшими точками по прямой) в метрах. В ответе укажите квадрат полученного значения.
5. Хозяин дома планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл), руб. | Прочее оборудование и монтаж, руб. | Средняя потребляемая мощность, кВт | Средний расход газа, м 3/час | Тариф | |
| Газовое отопление | 30 000 | 19 706 | 1,2 | – | 5,7 руб./м3 |
| Электрическое отопление | 20 000 | 15 000 | – | 5,7 | 5,5 руб./(кВт∙ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического оборудования?
Задание 8375
На рисунке изображена схема метро города N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Всего в метрополитене города N есть три станции, от которых тоннель ведёт только в одну сторону – это станции Дальняя, Верхняя и Звёздная. Антон живёт недалеко от станции Надежда.
1. Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других каких‐либо символов.
| Станции | Весёлая | Ветреная | Звёздная | Птичья |
| Цифры |
2. Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяжённостью 12,4 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 400 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
3. Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь (в км2), если длина кольцевой ветки равна 40 км. В ответе укажите значение выражения $$S\cdot \pi$$ .
4. Найдите расстояние (в км) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 17 км., расстояние от Звёздной до Смородиновой равно 10 км, а от Быстрой до Хоккейной – 12 км. Все расстояния даны по железной дороге.
5. Школьник Антон в среднем в месяц совершает 45 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Антон уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?
| Количество поездок | Стоимость карточки (руб) | Дополнительные условия |
| 1 | 40 | школьникам скидка 15% |
| 10 | 370 | школьникам скидка 10% |
| 30 | 1050 | школьникам скидка 10% |
| 50 | 1600 | нет |
| Не ограничено | 2000 | нет |
Расставим по номерам название станций согласно условию:
- Ветренная
- Быстрая
- Птичья
- Веселая
- Хоккейная
- Звездная
- Надежда
Тогда в ответ запишем 3174
Задание 8402
Владелец собирается провести ремонт своей квартиры. На плане (см. рисунок) изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Стол | Холодильник | Плита | Раковина |
2. Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки нужно купить, чтобы покрыть пол кухни?
3. Найдите площадь той части кухни, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
4. Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах.
5. Владелец квартиры выбирает холодильник из двух моделей А и Б. Цена холодильников и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт∙ч.
| Модель | Цена холодильника (руб) | Среднее потребление электроэнергии в сутки, кВт∙ч |
| А | 30 000 | 0,7 |
| Б | 28 000 | 0,9 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих холодильников? Ответ округлите до целого числа.
Задание 8454
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Горд Гранюк | Деревня Астрелка |
Хутор Южный |
Город Гусевск |
| Цифры |
2. Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
3. Найдите площадь (в км2), которую занимает заказник.
4. Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
5. Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐ магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | 190 | 180 | 3 |
| Шина вида «А» | 680 | 650 | 12 |
| Шина вида «Б» | 1680 | 1450 | 12 |
| Спица | 70 | 80 | 3 |
| Педаль вида «А» | 437 | 405 | 10 |
| Педаль вида «Б» | 860 | 750 | 10 |
| Тормоз вида «А» | 1130 | нет | 10 |
| Тормоз вида «Б» | нет | 2180 | 10 |
| Набор крепёжных изделий | 740 | 765 | 14 |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Задание 8506
На плане (см. рисунок) изображена местность, прилегающая к озеру Круглому. Для удобства план нанесён на квадратную сетку, сторона каждого квадрата которой равна 500 м. Населённые пункты обозначены на плане жирными точками. Рядом с озером Круглое находится болото, обозначенное на плане штриховкой. На болоте расположен хутор Камышино. От хутора Камышино проложена дорога к деревне Дубки, вокруг которой имеются дубовые рощи. Далее дорога идёт к селу Большое, расположенному по другую сторону озера от хутора Камышино. Село Большое соединено также дорогой с деревней Малая, обозначенной на плане цифрой 7. Деревня Малая, в свою очередь, соединена дорогой с деревней Дальней (отмечена цифрой 4). Преобладающая часть изображённой на плане местности – это поля, используемые для выращивания злаков.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Хутор Камышино | Село Большое | Озеро Круглое | Деревня Дубки |
| Цифры |
2. Автомобиль расходует в среднем 9 л топлива на 100 км пути. Сколько литров топлива израсходует автомобиль при поездке из хутора Камышино в деревню Малая по имеющимся дорогам?
3. Найдите площадь (в км2) болота, отмеченного на плане.
4. Найдите расстояние (в метрах) по прямой от хутора Камышино до села Большое.
5. Для улучшения сообщения между населёнными пунктами планируется построить ещё одну дорогу: из хутора Камышино в деревню Малая либо из хутора Камышино в деревню Дальняя. Дорога должна соединить населённые пункты по прямой. Цена прокладки дороги по полю равна 10 млн рублей за 1 км, по болоту – 20 млн рублей за 1 км. Из указанных двух вариантов дороги выберете тот, стоимость которого будет ниже. В ответе укажите стоимость (в млн рублей) выбранного варианта дороги.
Задание 8558
На плане (см. рисунок) представлен дизайн‐проект сквера в станице Лужки. Сторона большой клетки равна 2 метра. Участок, отведённый под сквер, имеет квадратную форму. По периметру участка планируется установить забор. С двух сторон сквера будут два входа. Если зайти в сквер, то справа от входа № 1 будет располагаться карусель, а слева – детский игровой комплекс, отмеченный на плане цифрой 5. Дом творчества будет находиться слева, если зайти через вход № 2, а зооуголок – справа. Центр сквера, отмеченный цифрой 4, планируется украсить фонтаном диаметром 2 метра и двумя цветочными клумбами. Рядом с детским игровым комплексом построят кафе, рядом с каруселью – кинотеатр площадью 64 м2. За кинотеатром будет оборудована тренажёрная площадка, отмеченная цифрой 8. На территории сквера шириной 2 м будут выложены тротуарной плиткой. Размером 1 м × 1 м. Аллея шириной 4 м располагается от входа № 1 до Дома творчества и выложена той же плиткой, что и дорожки.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Дом творчества | Кинотеатр | Кафе | Зооуголок |
| Цифры |
2. Тротуарная плитка продаётся в упаковках по 3 штуки. Сколько упаковок понадобится купить, чтобы выложить аллею от входа № 1 до Дома творчества?
3. Найдите площадь (в м2) земли, которую занимает Дом творчества.
4. Найдите наибольший возможный радиус карусели (в метрах).
5. При обсуждении, каким должен быть забор, рассматривалось два варианта: кованый или комбинированный. Цены на доставку оборудования и на установочные работы, а также стоимость изготовления одного погонного метра забора представлены в таблице. На сколько рублей общая стоимость кованного забора меньше общей стоимости комбинированного забора?
| Вариант забора | Стоимость доставки (руб.) | Стоимость установки (руб.) | Стоимость изготовления 1 погонного метра забора (руб.) |
| Кованый | 3 500 | 5 130 | 1000 |
| Комбинированный | 3 000 | 5 300 | 1300 |
Задание 8610
Сергей Васильевич – крупный учёный. На рисунке изображён план двухэтажного дома (сторона клетки соответствует 1 м), в котором он проживает с женой Валентиной Петровной и двумя детьми: Костей и Викой. На первом этаже гостиная – самая большая по площади комната. Кухня имеет вытянутую форму, её длина в два раза больше ширины, она тоже находится на первом этаже. Рядом с гостиной расположена столовая. Комната Кости расположена на втором этаже над кухней, его комната – соседняя с комнатой сестры Вики. Комната родителей расположена над столовой, рядом с ней просторный кабинет Сергея Васильевича.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Гостиная | Комната Кости | Кабинет | Кухня |
| Цифры |
2. На втором этаже расположен открытый балкон. На его бортике закреплены деревянные поручни. Определите их общую протяжённость в метрах.
3. Найдите площадь (в м2) комнаты Вики.
4. В каждой из пронумерованных комнат, кроме Костиной, два окна, а в Костиной – всего одно. Других окон нет. Площадь стекла для каждого окна составляет 3 м2. Стоимость окон при установке складывалась из стоимости стекла (3000 рублей за м2 окна) и стоимости монтажа и фурнитуры (7000 рублей за каждое окно). Определите общую стоимость всех окон и их установки. Ответ дайте в рублях.
5. После постройки дома денег на внутреннюю отделку осталось меньше, чем планировалось первоначально, поэтому пришлось экономить. В гостиной и столовой предполагалось класть паркетную доску, но обошлись ламинатом, а на сэкономленные деньги приобрели туристические путёвки в Крым. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое количество м 2 материала. Сколько рублей в результате удалось сэкономить на путёвки?
| Тип покрытия | Стоимость 1 м2 материала (руб.) | Стоимость укладки 1 м2 материала (руб.) | Количество материала в упаковке (м2) |
| Паркетная доска | 3 200 | 1 100 | 10 |
| Ламинат | 520 | 180 | 7 |
Задание 8805
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |
Задание 1.
Для листов бумаги форматов АЗ, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | АЗ | А4 | А5 | А6 |
Задание 2.
Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?
Задание 3.
Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
Задание 4.
Найдите площадь листа бумаги формата АЗ. Ответ дайте в квадратных сантиметрах.
Задание 5.
Найдите отношение длины большей стороны листа к меньшей у бумаги формата А1. Ответ дайте с точностью до десятых.
Задание 1.
Формат А3 – самый большой по размеру, а формат А6 – самый маленький. Выбираем в таблице по порядку номера, начиная с самого большого и заканчивая самым маленьким, получаем: 3 - А3; 2 – А4; 4 – А5; 1 – А6
Задание 2.
Пусть n – это число уменьшений формата от A0 до Ax. В нашем случае x=5 и, соответственно, n=5-0=5. Тогда число листов бумаги формата А5, получаемое из А0 можно вычислить по формуле: $$N=2^{n}=2^{5}=32$$ листа
Задание 3.
На рисунке видно, что большая сторона А2 равна двум меньшим сторонам А3: 297*2=594 мм
Задание 4.
По таблице лист формата А3 имеет размеры 420х297 мм и представляет собой прямоугольник 42*29,7 см. Значит, его площадь, равна: 42*29,7 см2, что составляет 1247,4 см2.
Задание 5.
Пропорции листа сохраняются независимо от формата, потому можно рассмотреть А6: $$\frac{148}{105}\approx 1,4$$
Задание 8806
Два друга Коля и Боря задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
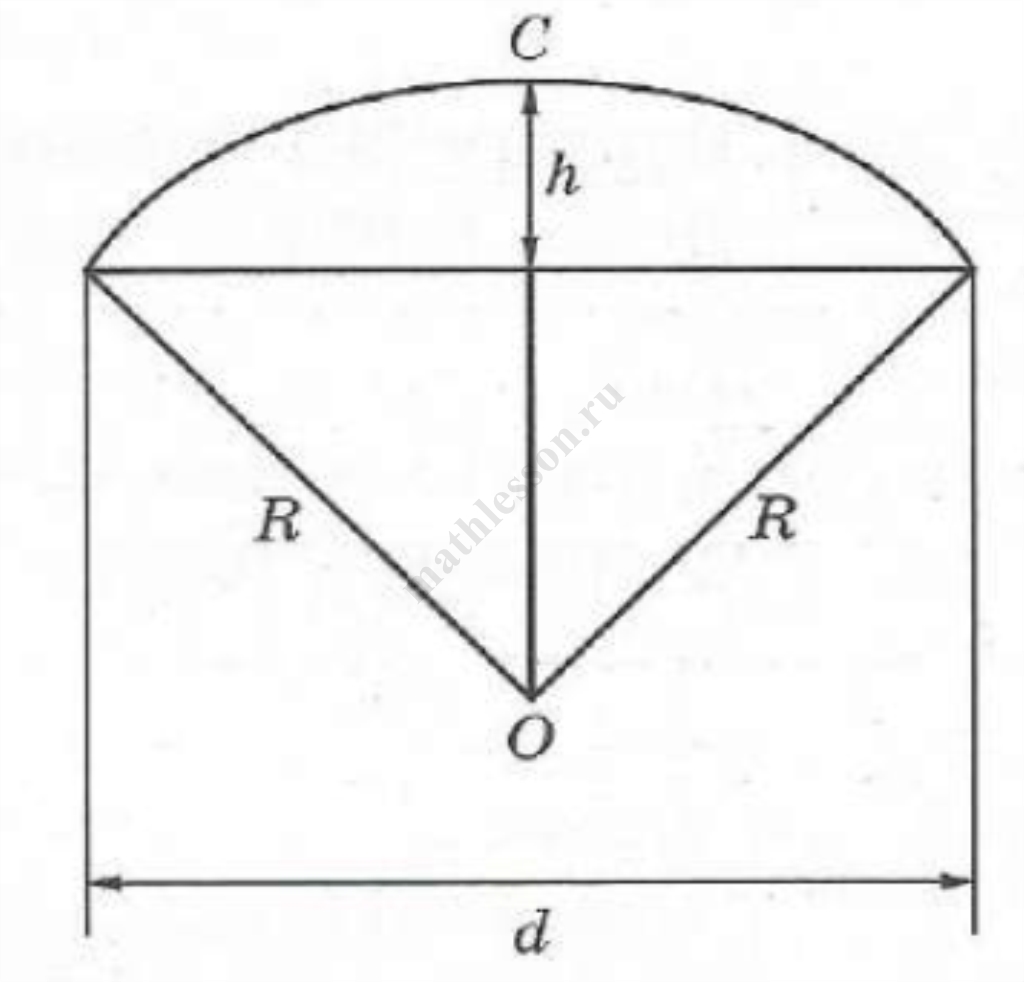
Коля и Боря сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 36 см. Высота купола зонта h (рис. 2) оказалась равна 20 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 116 см.
1. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,5 см.
2. Поскольку зонт сшит из треугольников, рассуждал Коля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Коли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 58,8 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Боря предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
4. Боря нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Бори. Число $$\pi$$ округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину 25 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 16 зонтов, таких же, как зонт, который был у Коли и Бори. Каждый треугольник с учётом припуска на швы имеет площадь 1100 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Задание 8832
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 148 | 210 |
| 2 | 210 | 297 |
| 3 | 105 | 148 |
| 4 | 297 | 420 |
Задание 1.
Для листов бумаги форматов АЗ, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | АЗ | А4 | А5 | А6 |
| Порядковые номера |
Задание 2.
Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата А2?
Задание 3.
Найдите длину большей стороны листа бумаги формата А1. Ответ дайте в миллиметрах
Задание 4.
Найдите площадь листа бумаги формата А4. Ответ дайте в квадратных сантиметрах.
Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 12 пунктов, на листе формата А5? Размер шрифта округлите до целого.
Задание 1.
Формат А3 – самый большой по размеру, а формат А6 – самый маленький. Выбираем в таблице по порядку номера, начиная с самого большого и заканчивая самым маленьким, получаем: 4 - А3; 2 – А4; 1 – А5; 3 – А6
Задание 2.
Пусть n – это число уменьшений формата от A2 до Ax. В нашем случае x=6 и, соответственно, n=6-2=4. Тогда число листов бумаги формата А6, получаемое из А2 можно вычислить по формуле листов: $$N=2^{n}=2^{4}=16$$
Задание 3.
Из рисунка видно, что набольшая сторона листа A1 равна двум наибольшим сторонам листа А3, а меньшая сторона А1 – двум меньшим сторонам листа А3. Из таблицы имеем значения размеров для А3, равные 297х420 мм. Тогда, для А1, получаем: 297∙2 х 420∙2 = 594 х 840 мм. И большая сторона имеет длину 840 мм.
Задание 4.
По таблице лист формата А4 имеет размеры 210х297 мм и представляет собой прямоугольник. Переведем миллиметры в сантиметры: 21х29,7 cм. Значит, его площадь, равна: $$S=21\cdot 29,7=623,7$$ cм2
Задание 5.
Большая сторона листа А4 равна 297 мм, а такая же сторона листа А5 – 210 мм, то есть, листа А4 больше листа А5 в $$\frac{297}{210}$$ раз. Следовательно, размер шрифта также нужно увеличить на это значение и взять равным: $$12\cdot \frac{297}{210}\approx 17$$ пунктов.
Задание 8950
На плане (см. рисунок) изображён парк культуры и отдыха города Малый. Сторона каждой клетки равна 2 м. Парк имеет прямоугольную форму. Зайти в парк можно через один из двух входов: западный или восточный. Если зайти в парк через западный вход, то слева будет расположено кафе «Полдник», а справа – детская площадка. Рядом с детской площадкой посажены каштаны. Рядом с восточным входом располагаются общественные туалеты и бадминтоновая площадка, обозначенная на плане цифрой 7. Помимо указанных объектов, в парке имеются фонтан (отмечен цифрой 2) и сцена. Все дорожки в парке ширину 2 м и вымощены тротуарной плиткой 1 м × 1 м. Между фонтаном и сценой имеется площадка, вымощенная такой же плиткой.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Сцена | Туалеты | Детская площадка | Кафе |
| Цифры |
2. Тротуарная плитка продаётся в упаковках по 10 штук. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку между сценой и фонтаном?
3. Найдите площадь (в м2), которую занимает бадминтонная площадка.
4. Детскую площадку планируется огородить заборчиком. Найдите длину этого заборчика в метрах.
5. Для остекления витрин кафе «Полдник» требуется заказать 30 одинаковых стёкол в одной из трёх фирм. Площадь каждого стекла 0,7 м2. В таблице приведены цены на стекло и на резку стекла. Сколько рублей будет стоить самый дешёвый заказ?
| Фирма | Цена стекла (руб./м2) | Резка стекла (руб./шт.) | Дополнительные условия |
| «Вени» | 560 | 35 | – |
| «Види» | 570 | 24 | При заказе на сумму свыше 15 000 рублей резка бесплатна |
| «Вици» | 600 | 13 | При заказе на сумму свыше 12 500 рублей резка бесплатна |
Задание 9004
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
Задание 1.
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Задание 2.
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
Задание 3.
Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Задание 4.
Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
Задание 5.
Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
Задание 9065
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см. Высота теплицы показана на рисунке отрезком HF.
Задание 1.
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 12 штук?
Задание 2.
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
Задание 3.
Найдите высоту теплицы. Ответ дайте в метрах с точностью до десятых.
Задание 4.
Найдите площадь участка, отведённого под теплицу. Ответ дайте в квадратных метрах. Результат округлите до целых.
Задание 5.
Сколько квадратных метров плёнки необходимо купить для передней и задней 1 стенок, если с учётом крепежа её нужно брать с запасом 10 %? Ответ округлите до десятых.
Задание 9069
Две подруги Ира и Юля задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Ира и Юля сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 40 см. Высота купола зонта h (рис. 2) оказалась равна 26 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 104 см.
1. Длина зонта в сложенном виде равна 26 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,5 см.
2. Поскольку зонт сшит из треугольников, рассуждала Ира, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Иры, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 55 см. Ответ дайте в квадратных сантиметрах.
3. Юля предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
4. Юля нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S=2\pi Rh$$, где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Юли. Число к округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину 30 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 27 зонтов, таких же, как зонт, который был у Иры и Юли. Каждый треугольник с учётом припуска на швы имеет площадь 1150 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Задание 9118
На плане (см. рисунок) изображена детская площадка, расположенная в общем дворе двух многоквартирных домов (сторона самой маленькой клетки на плане равна 1 м). Площадка предназначена как для детей младшего возраста, так и для школьников, поэтому она разделена на две отдельные части. При этом по краю зоны для малышей есть специальная дорожка, по которой можно кататься на роликах, машинках, велосипедах и просто бегать. Прямо перед скамейкой расположился игровой комплекс с горкой, домиком, лесенками, а слева от скамейки находится песочница, площадь которой равна 16 м2. Карусель отмечена на плане цифрой 6. Кроме того, в зоне для малышей имеются качели. В зоне для школьников находятся: комплекс уличных тренажёров, обозначенный цифрой 1, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. При этом поле для мини‐футбола имеет самую большую площадь, а верёвочный комплекс – самую маленькую.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Качели | Поле для мини‐футбола | Верёвочный комплекс | Песочница |
| Цифры |
2. Сколько кубических метров песка понадобилось, чтобы слой песка в песочнице был 20 см?
3. Найдите площадь (в м2), игрового комплекса для малышей.
4. Найдите длину (в метрах) диагонали поля для мини‐футбола.
Жители домов тщательно изучили современные материалы для мощения детской площадки. Было решено уложить в тех зонах, где есть риск получить травму, современное резиновое бесшовное покрытие. Такими зонами оказались площадка для малышей (за исключением песочницы, но включая дорожку), комплекс уличных тренажёров, площадка для активных игр, поле для мини‐футбола и верёвочный комплекс. Цены на материалы и монтаж приведены в таблице.
| Площадь (м2) | менее 100 | 100‐250 | 250‐500 | более 500 |
| Цена (руб./м2) | 1500 | 1470 | 1430 | 1400 |
5. Заказ на все площадки делается одновременно, и стоимость заказа зависит от суммарной площади. На сколько рублей дороже оказалось покрыть площадку для малышей, чем площадку для школьников?