ЕГЭ математика 2017. Разбор варианта Алекса Ларина № 197
Подробный разбор 1,2,3,4,5,6,7,8,9,10,11,12 задания тренировочного варианта ЕГЭ № 197 Ларина
Подробный разбор 13,14,15,16,17,18,19 задания тренировочного варианта ЕГЭ № 197 Ларина
Задание 2
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
580 мм.рт. ст. соответствует высота в два километра, это видно на графике
Задание 3
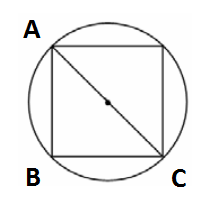
Диаметр окружности является диагональю квадрата. Пусть x - сторона квадрата. Тогда из треугольника ABC:
$$x^{2}+x^{2}=(3\sqrt{2})^{2}$$
Отсюда x=3
Задание 4
При каждом выстреле стрелок поражает мишень с вероятностью 0,8. В случае промаха стрелок делает повторный выстрел. Выстрелы повторяются до тех пор, пока мишень не будет поражена. Какое наименьшее количество выстрелов по мишени должен совершить стрелок, чтобы вероятность попадания в мишень составила более 0,995?
Так как вероятность попадания 0,8, то вероятность промаха равна 1-0,8=0,2. Рассмотрим ситуацию обратную поражению мишени - что ниразу не попадет. Если надо найти вероятность попадания более 0,995, значит можно рассматривать ситуацию промахов с вероятностью 1-0,995, то есть менее 0,005. Пусть совершено n выстрелов:
$$0.2^{n} \leq 0.005$$
Отсюда n⩾4. То есть необходимо не менее 4 выстрелов, чтобы вероятность всех промахов была менее 0,005, а значит и вероятность попадания более 0,995
Задание 5
В прямоугольном треугольнике гипотенуза равна $$6\sqrt{5}$$ , а тангенс одного из углов равен 2. Найдите меньший катет.
Тангенс угла, это отношение длин противолежащего катета к прилежащему, следовательно, мы можем взять один катет как x, а второй будет 2x(так как тангенс равен 2). Распишем теорему Пифагора с полученными значениями: $$x^{2}+(2x)^{2}=(6\sqrt{5})^{2}$$ $$5x^{2}=36*5$$ $$x^{2}=36$$ $$x=6 ; x=-6$$ Длина не может быть отрицательной, поэтому ответ 6.
Задание 6
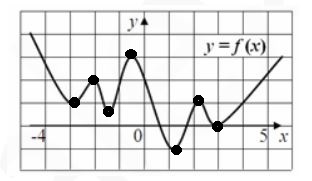
По графику функции у = f (x) определите количество точек на интервале (4;5), в которых касательная к графику параллельна оси абсцисс или совпадает с ней.
Если касательная параллельна оси ОХ, то производная равна 0. Производная равна нулю на данном графике функции в точках максимума и минимума ( они отмечены жирной точкой ). Их всего 7
Задание 7
Площадь поверхности сферы вычисляется по формуле: $$S=4\pi R^{2}$$ Объем шара вычисляется по формуле: $$V=\frac{4}{3}\pi R^{3}$$ Найдем сначала радиус сферы, зная площадь ее поверхности: $$4\pi R^{2} =24\sqrt[3]{\frac{\pi }{6}} $$ $$R^{2} =6\frac{\sqrt[3]{\frac{\pi }{6}}}{\pi} $$ $$R=\sqrt[3]{\frac{6}{\pi}} $$ Тогда объем шара будет равен: $$V=\frac{4}{3}\pi (\sqrt[3]{\frac{6}{\pi}})^{3}=8$$
Задание 8
Известно, что $$\frac{\cos x-\sin x}{\cos x+\sin x}=-0.8$$. Найдите $$ tg x $$
$$\frac{\cos x-\sin x}{\cos x+\sin x}=-0.8=\frac{-4}{5}$$ $$(\cos x-\sin x)*5=-4*(\cos x+\sin x)$$ $$5\cos x-5\sin x=-4*\cos x-4\sin x$$ $$9\cos x = \sin x $$ Поделим обе части на cos x $$9 = tg x $$
Задание 9
Добираясь из села в город, Виктор сначала 4 часа ехал на велосипеде со скоростью 12 км/ч, после чего велосипед сломался, и Виктору пришлось идти пешком еще 2 часа со скоростью 6 км/ч. С какой средней скоростью добирался от села до города Виктор? Ответ дайте в км/ч.
Задание 10
Имеется два сосуда равного объёма. Первый наполнен раствором соли с концентрацией 44%, второй –раствором соли с концентрацией 66%. Из каждого сосуда взяли по 5,5 л раствора; взятое из первого сосуда вылили во второй,а взятое из второго – в первый, после чего концентрации растворов в сосудах стали равны. Сколько литров раствора было в первом сосуде?
Задание 11
Найдите наибольшее значение функции $$f(x)=2^{x}(x+1)$$ , на отрезке [-1;2]
Найдем производную этой функции и приравняем ее к нулю:
$$f'(x)=2^{x}\ln 2(x+1)+2^{x}$$
$$2^{x}(\ln 2(x+1)+1)=0$$
$$\ln 2 * x+ \ln 2 + 1 = 0$$
$$x = -1 - \frac{1}{\ln 2}$$
Данное значение меньше -1, значит точка экстремума левее нашего промежутка, а это означает, в свою очередь, что на заданном промежутке функция монотонна. Если мы подставим ноль в производную, то получим, что на промежутке, где расположен ноль, производная больше нуля, значит функция возрастает. Поэтому наибольшее значение функции будет в конце промежутка.
$$f(2)=2^{2}(2+1)=4*3=12$$
Задание 13
В конусе с вершиной в точке $$P$$ высота равна 1, а образующая равна 2. В основании конуса провели диаметр $$CD$$ и перпендикулярную ему хорду $$AB$$. Известно, что хорда $$AB$$ удалена от центра основания на расстояние, равное 1.
Задание 15
Диагонали прямоугольника $$ABCD$$ пересекаются в точке $$O$$. Окружности $$\omega_1$$ и $$\omega_2$$ описаны около треугольников $$AOB$$ и $$BOC$$ соответственно. Пусть $$O_1$$ – центр окружности $$\omega_1$$, а $$O_2$$ – центр окружности $$\omega_2$$.
Задание 16
Гражданка Васильева вложила 44 млрд. рублей в два оффшорных банка на 3 года: часть денег в банк А, остальное в банк Б. Известно, что банк А ежегодно начисляет 10% годовых; банк Б в первый год начисляет 5% годовых, во второй – 10%, а в третий – 15%. Сколько рублей было вложено в каждый из банков, если через три года доход гражданки Васильевой от вложения денег составил 14520 млн. рублей.
Задание 18
б) Покажем, что
Что и требовалось доказать.