ЕГЭ математика 2017. Разбор варианта Алекса Ларина № 192
Более полный разбор 1-12 задания варианта 192 ЕГЭ Ларина
Разбор 13-19 задания
Поправки к 16,18,19 заданию
Задание 1
Жильцы 9‐этажки ежемесячно платят управляющей компании на капитальный ремонт дома по 250 рублей (с каждой квартиры). В доме 3 подъезда, на каждой площадке по 4 квартиры. Какую сумму выплачивают за год жильцы дома управляющей компании? Ответ дайте в рублях.
В каждом подъезде по: 9 * 4 = 36 квартир Всего в доме: 36 * 3 = 108 квартир В месяц с дома в сумме поступает: 108 * 250 = 27000 рублей Значит в год в итоге: 27 000 * 12 = 324 000
Задание 2
В 11А классе 25 учащихся. За контрольную по геометрии 5 человек получили отметку «5», 11 человек – «4», 8 человек – «3», и один ученик получил «2». Определите средний балл учащихся 11А класса за контрольную работу по геометрии.
Чтобы определить средний был, мы должны сложить все оценки и поделить на количество людей, то есть найти среднее арифметическое: $$\frac{5*5+11*4+8*3+1*2}{5+11+8+1}=3.8$$
Задание 3
Площадь большего круга в 4 раза больше площади маленького (так как радиус в два раза больше) => 4*4 = 16. Отсюда внешнего кольца : 16-4=12 Угол равен сорока пяти градусам, получается, что закрашенная область 315 градусов (360-45). Отсюда ее площадь: 12*315/360= 10.5
Задание 4
Генератор случайных чисел выводит на экран натуральное число, не превосходящее 100. Какова вероятность, что это число окажется простым?
Всего натуральных чисел, не превосходящих сто, собственно, сто штук. Простых чисел среди них 25. Следовательно, вероятность будет: $$\frac{25}{100}*4=0.25$$
Задание 5
Найдите периметр равностороннего треугольника, если радиус вписанной в него окружности равен $$2\sqrt{3}$$
Если радиус вписанной в него окружности равен $$2\sqrt{3}$$, то вся медиана этого треугольника будет $$2\sqrt{3}*3=6\sqrt{3}$$ (медиана в равностороннем треугольнике она и высота и биссекриса, следовательно, делится на радиус описанной и писанной окружностей, в отношении два к одному, поэтому радиус вписанной составляет одну треть от медианы) Сторона равностороннего треугольника будет равна : $$6\sqrt{3} : sin 60 =6\sqrt{3} :\frac{\sqrt{3}}{2} =12$$ Значит периметр равен 12*3=36
Задание 6
На графике производной функции у = f' / (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых угловой коэффициент касательной к графику функции f (x) положительный. В ответе укажите количество этих точек.
Угловой коэффициент касательной к графику это и есть значение производной, следовательно, мы ищем, где производная положительная. Так как дан нам график производной, то мы просто найдем количество точек, которые располагаются над осью ОХ: x1,x3,x4,x6 всего 4
Задание 7
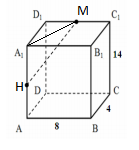
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно ВС=4, АВ=8, СС1=14. Найдите расстояние между серединами ребер АА1 и С1D1.
|
Для этого рассмотрим треугольник HA1M: HA1=0.5AA1=7 A1M=$$\sqrt{A_{1}D_{1}^{2}+D_{1}M^{2}}=\sqrt{4^{2}+4^{2}}=\sqrt{32}$$ MH=$$\sqrt{A_{1}H^{2}+A_{1}M^{2}}=\sqrt{7^{2}+32}=\sqrt{81}=9$$ |
Задание 8
Известно, что $$\log_a b *\log_b c = -5$$ . Найдите значение выражения $$\log_c a$$
$$\log_a b *\log_b c = \frac{1}{\log_b a}*\log_b c=\frac{\log_b c}{\log_b a}=\log_a c=-5$$ $$\log_c a=\frac{1}{\log_a c}=\frac{1}{-5}=-0.2$$
Задание 9
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле а=ω2R, где ω – угловая скорость (в с‐1), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с‐1, а центростремительное ускорение равно 650,25 м/с2.
Выразим R: $$R=\frac{a}{\omega ^{2}}=\frac{650.25}{8.5^{2}}=9$$
Задание 10
Свежие плоды содержат 60% воды. При сушке плоды теряют 40% своей влаги. Сколько килограммов свежих плодов потребуется для получения 1520 кг сухих?
Пусть S - первоначальная масса свежих плодов. Тогда воды в них X
При сушке теряется 40% воды, пусть эта масса Y:
Значит от первоначальной массы остается : S - 0.24S = 0.76S. Это и есть масса сухих плодов.
Найдем массу свежих: 0.76S=1520 S=1520/0.76=2000
Задание 11
Найдите наименьшее значение функции $$f(x)=(x^{2}-8x+8)*e^{2-x}$$ на отрезке [1; 7].
Найдем производную функции: $$f^{'}(x)=(2x-8)e^{2-x}+(-1)e^{2-x}(x^{2}-8x+8)=$$
$$=e^{2-x}(2x-8-x^{2}+8x-8)=e^{2-x}(-x^{2}+10x-16)$$
Приравняем производную к нулю:
$$e^{2-x}(-x^{2}+10x-16)=0$$ $$e^{2-x}=0$$
решений не имеет $$(-x^{2}+10x-16)=0$$ x1=2 и x2 =8
Отметим эти точки на координатной прямой и расставим знаки производной:
Точка минимума там, где производная меняет знак с - на +, то есть в точке 2
Подставим данное значение в первоначальную функцию и получим:
$$f(2)=(2^{2}-8*2+8)*e^{2-2}=(4-16+8)*1=-4$$
Задание 13
На продолжении высоты $$PO$$ правильной четырехугольной пирамиды $$PABCD$$ отмечена точка $$K$$ так, что $$OP=OK$$.
Задание 15
Дан квадрат $$ABCD$$. На сторонах $$AB$$ и $$BC$$ отмечены точки $$P$$ и $$K$$ соответственно, причем $$BP:AP=1:3$$, $$BK:CK=3:13$$.
Задание 16
Али‐Баба пришел в пещеру, где есть золото и алмазы. У Али‐Бабы с собой оказался мешок. Известно, что полный мешок золота весит 200 кг, полный мешок алмазов – 40 кг, а пустой мешок ничего не весит. Килограмм золота стоит 20 динаров, а килограмм алмазов – 60 динаров. Какую наибольшую сумму денег может выручить Али‐Баба за сокровища, если он может унести с собой не более 100 кг?
Задание 17
Найдите все значения $$a$$, при каждом из которых система $$\left\{\begin{matrix} x^2+y^2-4=2|x-2y|\\ x+y=a \end{matrix}\right.$$ имеет ровно два решения.
Задание 18
Дана последовательность $$(a_{n})$$: $$a_{n}=(n-1)\cdot n\cdot (n+1)+133$$.