ОГЭ
Задание 2671
На высоте AH треугольника ABC взята точка M. Докажите, что AB2–AC2=MB2–MC2.
$$AB^{2}-AC^{2}=MB^{2}-MC^{2}$$
|
1) из $$\bigtriangleup BMH$$ и $$\bigtriangleup CMH$$: $$MH^{2}=BM^{2}-BH^{2}=CM^{2}-CH^{2}$$ $$\Rightarrow$$ $$BM^{2}-CM^{2}=BH^{2}-CH^{2}$$ 2) из $$\bigtriangleup ABH$$ и $$\bigtriangleup AHC$$: $$AH^{2}=AB^{2}-BH^{2}=AC^{2}-CH^{2}$$ $$\Rightarrow$$ $$AB^{2}-AC^{2}=BH^{2}-CH^{2}$$ 3) из 1 и 2 $$BM^{2}-CM^{2}=BH^{2}-CH^{2}=AB^{2}-AC^{2}$$ $$\Rightarrow$$ $$AB^{2}-AC^{2}=BM^{2}-CM^{2}$$ |
 |
ч.т.д.
Задание 2775
В равнобедренном треугольнике АВС из концов основания АС проведены прямые, которые составляют с основанием равные углы и пересекаются в точке М. Докажите равенство треугольников АВМ и ВСМ.
|
1) $$\angle \alpha=\angle \beta$$ $$\Rightarrow$$ $$\bigtriangleup ACM$$ - равнобедренный $$\Rightarrow$$ $$AM=MC$$ 2) $$\angle A=\angle C$$; $$AB=BC$$; $$AM=MC$$ $$\Rightarrow$$ $$\bigtriangleup ABM=\bigtriangleup BMC$$ |
ч.т.д.
Задание 2929
Докажите, что если в треугольнике две высоты равны, то он равнобедренный.
Решение временно отсутствует, можете найти его в моем видео-разборе ( вначале варианта )
Задание 3019
Докажите, что если медиана треугольника совпадает с его биссектрисой, то этот треугольник равнобедренный.
|
AH - медиана и биссектриса $$\Rightarrow$$ $$\angle HAC=\angle HAB$$; BH=HC и АН - общая. По теореме косинусов: $$\left.\begin{matrix}\frac{AH}{\sin C}=\frac{HC}{\sin HAC}\\\frac{AH}{\sin B}=\frac{HB}{\sin BAH}\end{matrix}\right\}$$ $$\Rightarrow \sin C=\sin B\Rightarrow \angle C=\angle B$$ ч.т.д. |
Задание 2972
Докажите, что если у треугольника равны две высоты, то этот треугольник равнобедренный.
|
$$CH=AM$$ $$\bigtriangleup BCH=\bigtriangleup AMB$$ ($$\angle B$$ - общий катеты равны) $$\Rightarrow$$ $$AB=BC$$ $$\Rightarrow$$ $$\bigtriangleup ABC$$ - равнобедренный. ч. т. д. |
Задание 3845
В треугольнике АВС с тупым углом АСВ проведены высоты АА1 и ВВ1. Докажите, что треугольники А1СВ1 и АСВ подобны.
$$\bigtriangleup A_{1}CB_{1}\sim \bigtriangleup ACB$$
$$\angle A_{1}CA=\angle B_{1}CB$$ вертикальные
т.к. $$\bigtriangleup A_{1}AC$$ И $$\bigtriangleup BB_{1}C$$ прямоугольные, то из равенства их острых угловони подобные
$$\Rightarrow$$ $$\frac{A_{1}C}{CB_{1}}=\frac{AC}{CB}$$
$$\Rightarrow$$ $$\frac{A_{1}C}{AC}=\frac{CB_{1}}{CB}$$; $$\angle A_{1}CB_{1}=\angle ACB$$
$$\Rightarrow$$ $$\bigtriangleup ABC\sim \bigtriangleup A_{1}CB_{1}$$ по первому признаку
Задание 4653
На медиане KF треугольника MKP отмечена точка E. Докажите, что если EM=EP, то KM=KP.
Построим чертеж:

Задание 4803
Докажите, что сумма длин медиан треугольника меньше его периметра
На каждой стороне треугольника достроим параллелограмм, как показано на рисунке и введем обозначения: BC=a;AB=c;AC=b;CC1=mc;BB1=mb;AA1=ma
Задание 4871
На высоте AD треугольника ABC взята точка N. Докажите, что AB2 - AC2 = NB2 - NC2 .
Задание 5041
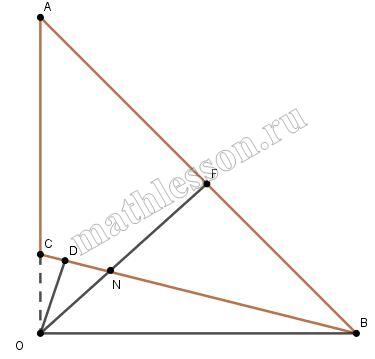
В треугольнике АВС угол АСВ тупой, $$BO\perp AC$$, $$OF\perp AB$$, $$OD\perp BC$$. Докажите, что $$\angle ACB=\angle DFB$$.
Пусть $$\angle A=\alpha$$; $$\angle B=\beta$$ $$\Rightarrow$$ $$\angle ACB=180-\angle\alpha-\angle\beta$$
1) $$\angle BCO=180-\angle C=\alpha+\beta$$ $$\Rightarrow$$ из $$\bigtriangleup OCB$$: $$\angle CBO=90^{\circ}-\angle BCO=90^{\circ}-\alpha-\beta$$
2) $$\bigtriangleup ODN\sim\bigtriangleup FNB$$ (прямоугольные); $$\angle DNO=\angle FNB$$ (как вертикал.); $$\Rightarrow$$ $$\frac{ON}{NB}=\frac{DN}{FN}$$ $$\Rightarrow$$ $$\frac{ON}{DN}=\frac{NB}{NF}$$ $$\Rightarrow$$ $$\angle DFN=\angle NBO=90^{\circ}-\alpha-\beta$$ $$\Rightarrow$$ $$\angle DFB=90^{\circ}+90^{\circ}-\alpha-\beta=180^{\circ}-\alpha-\beta=\angle ACB$$
ч.т.д.
Задание 5088
Докажите, что если в треугольнике два угла равны, то он равнобедренный.
Пусть $$BH\perp AC$$ $$\Rightarrow$$ $$\bigtriangleup ABH\sim\bigtriangleup BHC$$ по 2 углам, но т.к. $$BH$$ - общая ,то $$\bigtriangleup ABH=\bigtriangleup BHC$$ $$\Rightarrow$$ $$AB=BC$$
ч.т.д.
Задание 5557
В остроугольном треугольнике ABC проведены высоты AA1и BB1. Докажите, что углы AA1B1 и ABB1 равны
1) Пусть $$AA_{1}\cap BB_{1}=M$$, тогда $$\angle B_{1}MA=\angle A_{1}MB$$ (вертикальные)
2) $$\angle AB_{1}M=\angle MA_{1}B=90^{\circ}$$ $$\Rightarrow$$ $$\bigtriangleup AMB_{1}\sim\bigtriangleup A_{1}MB$$ $$\Rightarrow$$ $$\frac{B_{1}M}{A_{1}M}=\frac{AM}{MB}$$ ($$\ast$$)
3) $$\angle B_{1}MA_{1}=\angle AMB$$ (вертикальные), с учетом ($$\ast$$) $$\bigtriangleup B_{1}MA_{1}\sim\bigtriangleup AMB$$ $$\Rightarrow$$ $$\angle B_{1}A_{1}M=\angle MBA$$
Задание 5559
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
1) Пусть дан $$\bigtriangleup ABC$$, $$CM$$ - медиана $$\Rightarrow$$ $$AM=MB$$ ($$\star$$)
2) Пусть $$CH\perp AB$$, тогда $$S_{AMC}=\frac{1}{2}AM\cdot CH$$; $$S_{CMB}=\frac{1}{2}MB\cdot CH$$ с учетом ($$\star$$): $$S_{AMC}=S_{CMB}$$