ОГЭ
Задание 1765
Последовательность задана формулой $$c_{n}=n^{2}-1$$. Какое из указанных чисел является членом этой последовательности?
| 1) 1 |
| 2) 2 |
| 3) 3 |
| 4) 4 |
Данная последовательность возрастающая (в силу монотонности функции $$f_{x}=x^{2}-1$$, при $$x-in N$$. Найдем первые три члена последовательности:
$$c_{1}=1^{2}-1=0$$
$$c_{2}=2^{2}-1=3$$, как видим, третий вариант ответа является членом последовательности
$$c_{3}=3^{2}-1=8$$. Далее нет смысла рассматривать
Задание 1766
Последовательность задана формулой $$c_{n}=n+\frac{(-1)^{n}}{n}$$. Какое из следующих чисел не является членом этой последовательности?
| 1) $$2\frac{1}{2}$$ |
| 2) $$4\frac{1}{4}$$ |
| 3) $$5\frac{1}{5}$$ |
| 4) $$6\frac{1}{6}$$ |
Найдем второй, четвертый, пятый и шестой члены последовательности:
$$c_{2}=2+\frac{(-1)^{2}}{2}=2+\frac{1}{2}=2\frac{1}{2}$$
$$c_{4}=4+\frac{(-1)^{4}}{4}=4+\frac{1}{4}=4\frac{1}{4}$$
$$c_{5}=5+\frac{(-1)^{5}}{5}=5-\frac{1}{5}=4\frac{4}{5}\neq 5\frac{1}{5}$$, следовательно, третий вариант не является членом последовательности
$$c_{6}=6+\frac{(-1)^{6}}{6}=6+\frac{1}{6}=6\frac{1}{6}$$
Задание 1767
Какое из указанных чисел не является членом последовательности $$a_{n}=\frac{(-1)^{n}}{n}$$?
| 1) $$\frac{1}{2}$$ |
| 2) $$-\frac{1}{3}$$ |
| 3) $$\frac{1}{16}$$ |
| 4) $$\frac{1}{17}$$ |
Найдем второй, третий, шестнадцатый и семнадцатый члена последовательности:
$$a_{2}=\frac{(-1)^{2}}{2}=\frac{1}{2}$$
$$a_{3}=\frac{(-1)^{3}}{3}=-\frac{1}{3}$$
$$a_{16}=\frac{(-1)^{16}}{16}=\frac{1}{16}$$
$$a_{17}=\frac{(-1)^{17}}{17}=-\frac{1}{17}\neq \frac{1}{17}$$, следовательно, четвертый вариант ответа не является членом последовательности.
Задание 1769
Последовательности заданы несколькими первыми членами. Одна из них — арифметическая прогрессия. Укажите ее.
Для того, чтобы числовая последовательность была арифметической прогрессией, необходимо выполнение условия $$d=a_{n+1}-a_{n}$$ для всех членов последовательности:
1) 1; 2; 3; 5; ... $$d_{1}=2-1=1 ; d_{2}=3-2=1 ; d_{3}=5-3=2$$, как видим $$d_{3}\neq d_{2}$$, следовательно, это не арифметическая прогрессия
2) 1; 2; 4; 8; ... $$d_{1}=2-1=1 ; d_{2}=4-2=2$$, как видим $$d_{2}\neq d_{1}$$, следовательно, это не арифметическая прогрессия
3) 1; 3; 5; 7; ... $$d_{1}=3-1=2 ; d_{2}=5-3=2 ; d_{3}=7-5=2$$, как видим $$d_{3}=d_{2}=d_{1}$$, следовательно, это арифметическая прогрессия
4) 1; $$\frac{1}{2}; \frac{2}{3}; \frac{3}{4}$$; ... $$d_{1}=\frac{2}{3}-\frac{1}{2}=\frac{1}{6} ; d_{2}=\frac{3}{4}-\frac{2}{3}=\frac{1}{12} $$, как видим $$d_{2}\neq d_{1}$$, следовательно, это не арифметическая прогрессия
Задание 1770
Чтобы числовая последовательность была геометрической прогрессией необходимо выполнение условия для всех членов последовательности: $$q=\frac{b_{n+1}}{b_{n}}$$
Задание 1771
Задание 1772
Последовательность задана условиями $$c_{1}=-3$$, $$c_{n+1}=c_{n}-1$$. Найдите $$c_{7}$$.
В данном случае дана арифметическая прогрессия, найдем ее разность: $$d=c_{n+1}-c_{n}=c_{n}-1-c_{n}=-1$$. Найдем 7ой член прогрессии, воспользовавшись формулой n-го члена арифметической прогрессии: $$c_{7}=-3+(-1)(7-1)=-9$$
Задание 1773
Последовательность задана условиями $$b_{1}=4$$, $$b_{n+1}=-\frac{1}{b_{n}}$$. Найдите $$b_{7}$$.
Задание 1774
Последовательность задана формулой $$a_{n}=\frac{34}{n+1}$$. Сколько членов в этой последовательности больше 6?
Необходимо найти все значения $$n\in N$$, при которых $$a_{n}>6$$: решим неравенство $$\frac{34}{n+1}>6\Leftrightarrow$$$$\frac{34-6(n+1)}{n+1}>0\Leftrightarrow$$$$\frac{28-6n}{n+1}>0$$. Начертим координатную прямую и отметим значения Х, когда числитель и знаменатель равны нулю (неравенство строгое, потому обе точки будут пустые) и знаки значений ,которые принимает выражение : $$\frac{28-6n}{n+1}$$ на полученных промежутках:
Нам необходим промежуток тот, где получается положительные значения, то есть $$(-1;\frac{28}{6})$$. Так же необходимо учитывать, что $$n\in N$$, так как это порядковый номер. Тогда натуральных чисел на полученном промежутке 4 (1;2;3;4).
Задание 1775
Сколько натуральных чисел n удовлетворяет неравенству $$\frac{40}{n+1}>2$$?
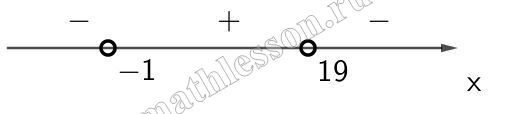
Решим данное неравенство: $$\frac{40}{n+1}>2\Leftrightarrow$$$$\frac{40-2(n+1)}{n+1}>0\Leftrightarrow$$$$\frac{38-2n}{n+1}>0$$. Начертим координатную прямую и отметим значения Х, когда числитель и знаменатель равны нулю (неравенство строгое, потому обе точки будут пустые) и знаки значений ,которые принимает выражение : $$\frac{38-2n}{n+1}$$ на полученных промежутках:
Нам необходим промежуток тот, где получается положительные значения, то есть $$(-1;19)$$. Так же необходимо учитывать, что $$n\in N$$, так как это порядковый номер. Тогда натуральных чисел на полученном промежутке 18.
Задание 2761
Последовательность $$(b_{n})$$ задана условиями $$b_{1}=-5$$, $$b_{n+1}=-2\frac{1}{b_{n}}$$. Найдите $$b_{3}$$
$$b_{1}=-5$$; $$b_{n+1}=-2\frac{1}{b_{n}}$$ $$b_{2}=-2\cdot\frac{1}{b_{1}}=-2\cdot\frac{1}{-5}=\frac{2}{5}$$ $$b_{3}=-2\cdot\frac{1}{\frac{2}{5}}=-5$$
Задание 2915
Последовательность ($$a_{n}$$) задана условиями $$a_{1}=5 , a_{n+1}=a_{n}-3$$. Найти $$a_{10}$$
Есть два варианта решения, мы можем находить поочередно все члены со второго по десятый, путем вычитания из предыдущего числа 3. То есть, второй у нас будет равен первый минус 3: 5-3=2. Третий же равен, второй минус 3 = 2-3=-1. И так далее до 10: 5-3-3-3-3-3-3-3-3-3=5-27=-22
Или же воспользуемся формулами арифметической прогрессии. Число, которое мы будем вычитать называется разностью арифметической прогрессии, и оно равно -3: d=-3; n-порядковый номер, у нас n=10. Тогда: $$a_{n}=a_{1}+d(n-1)=5-3*(10-1)=5-27=-22$$
Задание 3395
Последовательность $$(b_{n})$$ задана условиями $$b_{1}=-5$$, $$b_{n+1}=-2\cdot\frac{1}{b_{n}}$$ Найдите b3
$$b_{1}=-5$$ $$b_{2}=-2\cdot\frac{1}{b_{1}}=-2\cdot\frac{1}{-5}=\frac{2}{5}$$ $$b_{3}=-2\cdot\frac{1}{b_{2}}=-2\cdot\frac{1}{\frac{2}{5}}=-5$$
Задание 3554
Последовательность$$(a_{n})$$ задана условиями $$a_{1}=1$$, $$a_{n+1}=a_{n}-5$$. Найдите $$a_{10}$$
$$d=-5$$; $$n=10$$; $$a_{1}=1$$ $$a_{n}=a_{1}+d(n-1)$$ $$a_{10}=1-5\cdot(10-1)=1-45=-44$$
Задание 3982
Последовательность $$(a_{n}$$ задана условиями $$a_{1}=-3,a_{n+1}=a_{n}+3$$. Найдите $$a_{10}$$
$$a_[1}=-3$$
$$a_{n+1}=a_{n}+3$$
$$d=a_{n+1}-a_{n}=a_{n+3}-a_{n}=3$$
$$a_{n}=a_{1}+d(n-1)$$
$$a_{10}=-3+3\cdot(10-1)=-3+27=24$$